NEET-XII-Physics
13: Nuclei
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #5 - Nuclei
- #1
- #1-aTwo stable isotopes of lithium
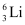 and
and  have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.Ans : Mass of lithium isotope
have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.Ans : Mass of lithium isotope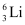 , m1 = 6.01512 u
, m1 = 6.01512 u
Mass of lithium isotope , m2 = 7.01600 u
, m2 = 7.01600 u
Abundance of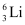 , η1= 7.5%
, η1= 7.5%
Abundance of , η2= 92.5%
, η2= 92.5%
The atomic mass of lithium atom is given as:

- #1-bBoron has two stable isotopes,
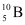 and
and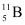 . Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of
. Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of 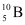 and
and 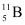 .Ans : Mass of boron isotope
.Ans : Mass of boron isotope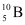 , m1 = 10.01294 u
, m1 = 10.01294 u
Mass of boron isotope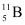 , m2 = 11.00931 u
, m2 = 11.00931 u
Abundance of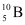 , η1 = x%
, η1 = x%
Abundance of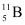 , η2= (100 - x)%
, η2= (100 - x)%
Atomic mass of boron, m = 10.811 u
The atomic mass of boron atom is given as:

And 100 - x = 80.11%
Hence, the abundance of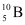 is 19.89% and that of
is 19.89% and that of 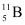 is 80.11%.
is 80.11%.
- Qstn #2The three stable isotopes of neon:
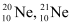 and
and
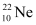 have respective abundances of 90.51%, 0.27% and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u and 21.99 u, respectively. Obtain the average atomic mass of neon.
have respective abundances of 90.51%, 0.27% and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u and 21.99 u, respectively. Obtain the average atomic mass of neon.
Ans : Atomic mass of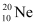 , m1= 19.99 u
, m1= 19.99 u
Abundance of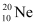 , η1 = 90.51%
, η1 = 90.51%
Atomic mass of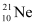 , m2 = 20.99 u
, m2 = 20.99 u
Abundance of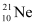 , η2 = 0.27%
, η2 = 0.27%
Atomic mass of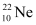 , m3 = 21.99 u
, m3 = 21.99 u
Abundance of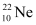 , η3 = 9.22%
, η3 = 9.22%
The average atomic mass of neon is given as:
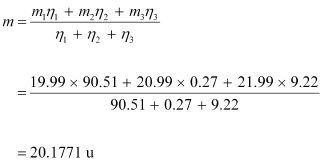
- Qstn #3Obtain the binding energy (in MeV) of a nitrogen nucleus
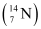 , given
, given 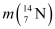 =14.00307 u
=14.00307 u
Ans : Atomic mass of nitrogen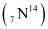 , m = 14.00307 u
, m = 14.00307 u
A nucleus of nitrogen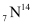 contains 7 protons and 7 neutrons.
contains 7 protons and 7 neutrons.
Hence, the mass defect of this nucleus, Δm = 7mH + 7mn - m
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn= 1.008665 u
∴Δm = 7 × 1.007825 + 7 × 1.008665 - 14.00307
= 7.054775 + 7.06055 - 14.00307
= 0.11236 u
But 1 u = 931.5 MeV/c2
∴Δm = 0.11236 × 931.5 MeV/c2
Hence, the binding energy of the nucleus is given as:
Eb = Δmc2
Where,
c = Speed of light
∴Eb = 0.11236 × 931.5
= 104.66334 MeV
Hence, the binding energy of a nitrogen nucleus is 104.66334 MeV.
- Qstn #4Obtain the binding energy of the nuclei
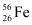 and
and 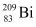 in units of MeV from the following data:
in units of MeV from the following data:
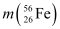 = 55.934939 u
= 55.934939 u 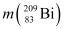 = 208.980388 u
= 208.980388 u
Ans : Atomic mass of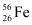 , m1 = 55.934939 u
, m1 = 55.934939 u
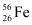 nucleus has 26 protons and (56 - 26) = 30 neutrons
nucleus has 26 protons and (56 - 26) = 30 neutrons
Hence, the mass defect of the nucleus, Δm = 26 × mH + 30 × mn - m1
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm = 26 × 1.007825 + 30 × 1.008665 - 55.934939
= 26.20345 + 30.25995 - 55.934939
= 0.528461 u
But 1 u = 931.5 MeV/c2
∴Δm = 0.528461 × 931.5 MeV/c2
The binding energy of this nucleus is given as:
Eb1 = Δmc2
Where,
c = Speed of light
∴Eb1 = 0.528461 × 931.5.gif)
= 492.26 MeV
Average binding energy per nucleon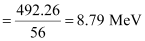
Atomic mass of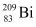 , m2 = 208.980388 u
, m2 = 208.980388 u
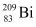 nucleus has 83 protons and (209 - 83) 126 neutrons.
nucleus has 83 protons and (209 - 83) 126 neutrons.
Hence, the mass defect of this nucleus is given as:
Δm‘ = 83 × mH + 126 × mn - m2
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm‘ = 83 × 1.007825 + 126 × 1.008665 - 208.980388
= 83.649475 + 127.091790 - 208.980388
= 1.760877 u
But 1 u = 931.5 MeV/c2
∴Δm‘ = 1.760877 × 931.5 MeV/c2
Hence, the binding energy of this nucleus is given as:
Eb2 = Δm‘c2
= 1.760877 × 931.5.gif)
= 1640.26 MeV
Average bindingenergy per nucleon =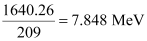
- Qstn #5A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of
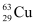 atoms (of mass 62.92960 u).
atoms (of mass 62.92960 u).
Ans : Mass of a copper coin, m’ = 3 g
Atomic mass of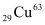 atom, m = 62.92960 u
atom, m = 62.92960 u
The total number of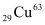 atoms in the coin
atoms in the coin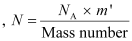
Where,
NA = Avogadro’s number = 6.023 × 1023 atoms /g
Mass number = 63 g
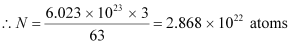
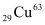 nucleus has 29 protons and (63 - 29) 34 neutrons
nucleus has 29 protons and (63 - 29) 34 neutrons
∴Mass defect of this nucleus, Δm‘ = 29 × mH + 34 × mn - m
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm‘ = 29 × 1.007825 + 34 × 1.008665 - 62.9296
= 0.591935 u
Mass defect of all the atoms present in the coin, Δm = 0.591935 × 2.868 × 1022
= 1.69766958 × 1022 u
But 1 u = 931.5 MeV/c2
∴Δm = 1.69766958 × 1022 × 931.5 MeV/c2
Hence, the binding energy of the nuclei of the coin is given as:
Eb= Δmc2
= 1.69766958 × 1022 × 931.5.gif)
= 1.581 × 1025 MeV
But 1 MeV = 1.6 × 10-13 J
Eb = 1.581 × 1025 × 1.6 × 10-13
= 2.5296 × 1012 J
This much energy is required to separate all the neutrons and protons from the given coin.
- Qstn #6Write nuclear reaction equations for
(i) α-decay of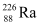 (ii) α-decay of
(ii) α-decay of 
(iii) β--decay of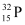 (iv) β--decay of
(iv) β--decay of 
(v) β+-decay of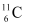 (vi) β+-decay of
(vi) β+-decay of 
(vii) Electron capture of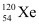 Ans : α is a nucleus of helium
Ans : α is a nucleus of helium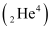 and β is an electron (e- for β- and e+ for β+). In every α-decay, there is a loss of 2 protons and 4 neutrons. In every β+-decay, there is a loss of 1 proton and a neutrino is emitted from the nucleus. In every β--decay, there is a gain of 1 proton and an antineutrino is emitted from the nucleus.
and β is an electron (e- for β- and e+ for β+). In every α-decay, there is a loss of 2 protons and 4 neutrons. In every β+-decay, there is a loss of 1 proton and a neutrino is emitted from the nucleus. In every β--decay, there is a gain of 1 proton and an antineutrino is emitted from the nucleus.
For the given cases, the various nuclear reactions can be written as:
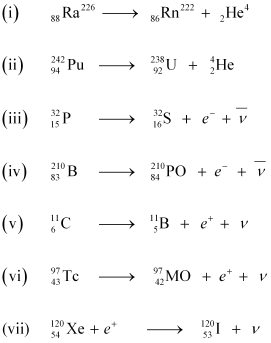
- Qstn #7A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to
a) 3.125%, b) 1% of its original value?
Ans : Half-life of the radioactive isotope = T years
Original amount of the radioactive isotope = N0
a) After decay, the amount of the radioactive isotope = N
It is given that only 3.125% of N0 remains after decay. Hence, we can write:

Where,
λ = Decay constant
t = Time
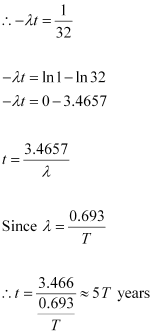
Hence, the isotope will take about 5T years to reduce to 3.125% of its original value.
b) After decay, the amount of the radioactive isotope = N
It is given that only 1% of N0 remains after decay. Hence, we can write:
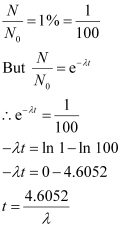
Since, λ = 0.693/T
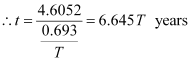
Hence, the isotope will take about 6.645T years to reduce to 1% of its original value.
- Qstn #8The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive
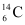 present with the stable carbon isotope
present with the stable carbon isotope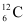 . When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of
. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of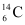 , and the measured activity, the age of the specimen can be approximately estimated. This is the principle of
, and the measured activity, the age of the specimen can be approximately estimated. This is the principle of 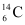 dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
dating used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilisation.
Ans : Decay rate of living carbon-containing matter, R = 15 decay/min
Let N be the number of radioactive atoms present in a normal carbon- containing matter.
Half life of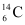 ,
, 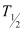 = 5730 years
= 5730 years
The decay rate of the specimen obtained from the Mohenjodaro site:
R‘ = 9 decays/min
Let N’ be the number of radioactive atoms present in the specimen during the Mohenjodaro period.
Therefore, we can relate the decay constant, λand time, t as:
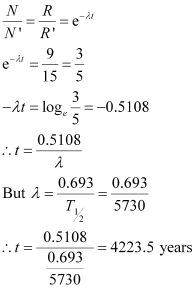
Hence, the approximate age of the Indus-Valley civilisation is 4223.5 years.
- Qstn #9Obtain the amount of
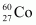 necessary to provide a radioactive source of 8.0 mCi strength. The half-life of
necessary to provide a radioactive source of 8.0 mCi strength. The half-life of 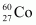 is 5.3 years.
is 5.3 years.
Ans : The strength of the radioactive source is given as:

Where,
N = Required number of atoms
Half-life of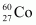 ,
, .gif) = 5.3 years
= 5.3 years
= 5.3 × 365 × 24 × 60 × 60
= 1.67 × 108 s
For decay constant λ, we have the rate of decay as:
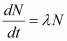
Where, λ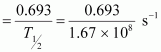

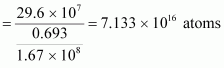
For :
:
Mass of 6.023 × 1023 (Avogadro’s number) atoms = 60 g
∴Mass of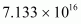 atoms
atoms 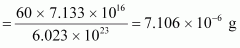
Hence, the amount of necessary for the purpose is 7.106 × 10-6 g.
necessary for the purpose is 7.106 × 10-6 g.
- Qstn #10The half-life of
 is 28 years. What is the disintegration rate of 15 mg of this isotope?
is 28 years. What is the disintegration rate of 15 mg of this isotope?
Ans : Half life of ,
, 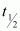 = 28 years
= 28 years
= 28 × 365 × 24 × 60 × 60
= 8.83 × 108 s
Mass of the isotope, m = 15 mg
90 g of atom contains 6.023 × 1023 (Avogadro’s number) atoms.
atom contains 6.023 × 1023 (Avogadro’s number) atoms.
Therefore, 15 mg of contains:
contains:

Rate of disintegration,.gif)
Where,
λ = Decay constant
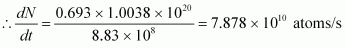
Hence, the disintegration rate of 15 mg of the given isotope is 7.878 × 1010 atoms/s.
- Qstn #11Obtain approximately the ratio of the nuclear radii of the gold isotope
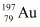 and the silver isotope
and the silver isotope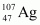 .
.
Ans : Nuclear radius of the gold isotope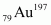 = RAu
= RAu
Nuclear radius of the silver isotope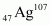 = RAg
= RAg
Mass number of gold, AAu = 197
Mass number of silver, AAg = 107
The ratio of the radii of the two nuclei is related with their mass numbers as:

Hence, the ratio of the nuclear radii of the gold and silver isotopes is about 1.23.