HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

13: Nuclei

 page 2

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • #12-a
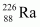    and
    Ans : Alpha particle decay of 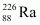emits a helium nucleus. As a result, its mass number reduces to (226 - 4) 222 and its atomic number reduces to (88 - 2) 86. This is shown in the following nuclear reaction.



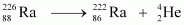
    Q-value of

    emitted α-particle = (Sum of initial mass - Sum of final mass) c2

    Where,

    c = Speed of light

    It is given that:



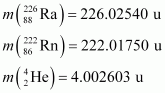
    Q-value = [226.02540 - (222.01750 + 4.002603)] u c2

    = 0.005297 u c2

    But 1 u = 931.5 MeV/c2

    ∴Q = 0.005297 × 931.5 ≈ 4.94 MeV

    Kinetic energy of the α-particle


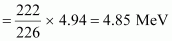
  • #12-b
    .

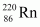    Given

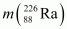    = 226.02540 u, 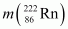= 222.01750 u,

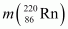    = 220.01137 u, 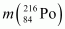= 216.00189 u.
    Ans : Alpha particle decay of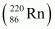 is shown by the following nuclear reaction.



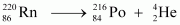
    It is given that:

    Mass of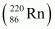 = 220.01137 u

    Mass of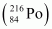 = 216.00189 u

    ∴Q-value =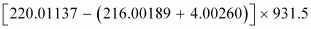

    ≈ 641 MeV

    Kinetic energy of the α-particle

    = 6.29 MeV
  • Qstn #13
    The radionuclide 11C decays according to



    The maximum energy of the emitted positron is 0.960 MeV.

    Given the mass values:



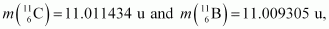
    calculate Q and compare it with the maximum energy of the positron emitted
    Ans : The given nuclear reaction is:



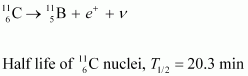
    Atomic mass of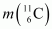 = 11.011434 u

    Atomic mass of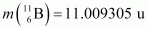

    Maximum energy possessed by the emitted positron = 0.960 MeV

    The change in the Q-value (ΔQ) of the nuclear masses of the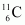 nucleus is given as:



    Where,

    me = Mass of an electron or positron = 0.000548 u

    c = Speed of light

    m’ = Respective nuclear masses

    If atomic masses are used instead of nuclear masses, then we have to add 6 me in the case of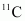and 5 me in the case of.

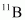    Hence, equation (1) reduces to:



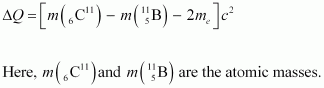
    ∴ΔQ = [11.011434 - 11.009305 - 2 × 0.000548] c2

    = (0.001033 c2) u

    But 1 u = 931.5 Mev/c2

    ∴ΔQ = 0.001033 × 931.5 ≈ 0.962 MeV

    The value of Q is almost comparable to the maximum energy of the emitted positron.
  • Qstn #14
    The nucleus 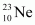decays by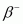emission. Write down the 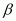decay equation and determine the maximum kinetic energy of the electrons emitted. Given that:

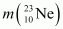    = 22.994466 u

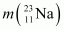    = 22.989770 u.
    Ans : In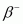 emission, the number of protons increases by 1, and one electron and an antineutrino are emitted from the parent nucleus.

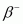    emission of the nucleus 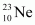is given as:



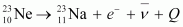
    It is given that:

    Atomic mass of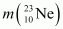 = 22.994466 u

    Atomic mass of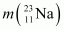 = 22.989770 u

    Mass of an electron, me = 0.000548 u

    Q-value of the given reaction is given as:



    There are 10 electrons in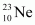 and 11 electrons in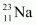. Hence, the mass of the electron is cancelled in the Q-value equation.



    The daughter nucleus is too heavy as compared to and . Hence, it carries negligible energy. The kinetic energy of the antineutrino is nearly zero. Hence, the maximum kinetic energy of the emitted electrons is almost equal to the Q-value, i.e., 4.374 MeV.
  • Qstn #15
    The Q value of a nuclear reaction A + b → C + d is defined by

    Q = [ mA+ mb- mC- md]c2 where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
  • Ans : The given nuclear reaction is:



    It is given that:

    Atomic mass

    Atomic mass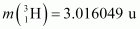

    Atomic mass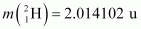

    According to the question, the Q-value of the reaction can be written as:



    The negativeQ-value of the reaction shows that the reaction is endothermic.
  • Qstn #15-ii


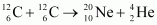
    Atomic masses are given to be


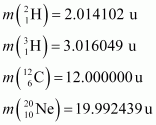
    Ans : The given nuclear reaction is:



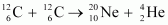
    It is given that:

    Atomic mass of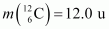

    Atomic mass of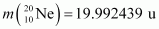

    Atomic mass of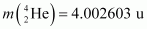

    The Q-value of this reaction is given as:



    The positive Q-value of the reaction shows that the reaction is exothermic.
  • Qstn #16
    Suppose, we think of fission of a 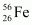nucleus into two equal fragments,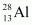. Is the fission energetically possible? Argue by working out Q of the process. Given 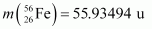and.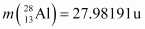
    Ans : The fission of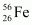 can be given as:



    It is given that:

    Atomic mass of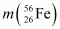 = 55.93494 u

    Atomic mass of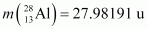

    The Q-value of this nuclear reaction is given as:



    The Q-value of the fission is negative. Therefore, the fission is not possible energetically. For an energetically-possible fission reaction, the Q-value must be positive.
  • Qstn #17
    The fission properties of 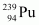are very similar to those of.

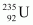    The average energy released per fission is 180 MeV. How much energy, in MeV, is released if all the atoms in 1 kg of pure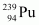 undergo fission?
    Ans : Average energy released per fission of,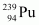

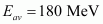
    Amount of pure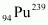, m = 1 kg = 1000 g

    NA= Avogadro number = 6.023 × 1023

    Mass number of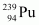= 239 g

    1 mole of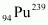 contains NA atoms.

    ∴m g of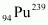 contains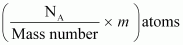



    ∴Total energy released during the fission of 1 kg of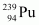is calculated as:



    Hence,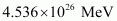 is released if all the atoms in 1 kg of pure 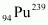undergo fission.
  • Qstn #18
    A 1000 MW fission reactor consumes half of its fuel in 5.00 y. How much

    did it contain initially? Assume that the reactor operates 80% of the time, that all the energy generated arises from the fission of and that this nuclide is consumed only by the fission process.
    Ans : Half life of the fuel of the fission reactor,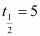 years

    = 5 × 365 × 24 × 60 × 60 s

    We know that in the fission of 1 g of nucleus, the energy released is equal to 200 MeV.

    1 mole, i.e., 235 g of contains 6.023 × 1023 atoms.

    ∴1 g contains

    The total energy generated per gram ofis calculated as:



    The reactor operates only 80% of the time.

    Hence, the amount of consumed in 5 years by the 1000 MW fission reactor is calculated as:



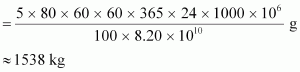
    ∴Initial amount of = 2 × 1538 = 3076 kg
  • Qstn #19
    How long can an electric lamp of 100W be kept glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction as


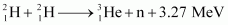
    Ans : The given fusion reaction is:



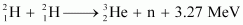
    Amount of deuterium, m = 2 kg

    1 mole, i.e., 2 g of deuterium contains 6.023 × 1023 atoms.

    ∴2.0 kg of deuterium contains

    It can be inferred from the given reaction that when two atoms of deuterium fuse, 3.27 MeV energy is released.

    ∴Total energy per nucleus released in the fusion reaction:



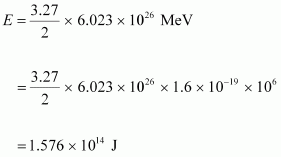
    Power of the electric lamp, P = 100 W = 100 J/s

    Hence, the energy consumed by the lamp per second = 100 J

    The total time for which the electric lamp will glow is calculated as:


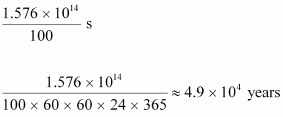
  • Qstn #20
    Calculate the height of the potential barrier for a head on collision of two deuterons. (Hint: The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm.)
    Ans : When two deuterons collide head-on, the distance between their centres, d is given as:

    Radius of 1st deuteron + Radius of 2nd deuteron

    Radius of a deuteron nucleus = 2 fm = 2 × 10-15 m

    ∴d = 2 × 10-15 + 2 × 10-15 = 4 × 10-15 m

    Charge on a deuteron nucleus = Charge on an electron = e = 1.6 × 10-19 C

    Potential energy of the two-deuteron system:



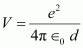
    Where,

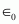    = Permittivity of free space



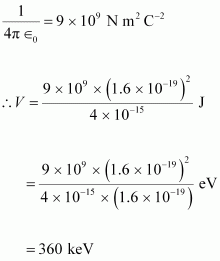
    Hence, the height of the potential barrier of the two-deuteron system is

    360 keV.
  • Qstn #21
    From the relation R = R0A1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e. independent of A).
    Ans : We have the expression for nuclear radius as:

    R = R0A1/3

    Where,

    R0 = Constant.

    A = Mass number of the nucleus

    Nuclear matter density,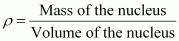

    Let m be the average mass of the nucleus.

    Hence, mass of the nucleus = mA



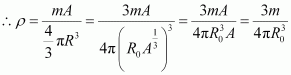
    Hence, the nuclear matter density is independent of A. It is nearly constant.
  • Qstn #22
    For the 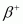(positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K-shell, is captured by the nucleus and a neutrino is emitted).



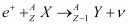
    Show that if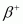 emission is energetically allowed, electron capture is necessarily allowed but not vice-versa.
    Ans : Let the amount of energy released during the electron capture process be Q1. The nuclear reaction can be written as:



    Let the amount of energy released during the positron capture process be Q2. The nuclear reaction can be written as:



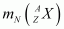    = Nuclear mass of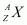

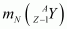    = Nuclear mass of

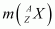    = Atomic mass of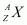

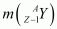    = Atomic mass of

    me = Mass of an electron

    c = Speed of light

    Q-value of the electron capture reaction is given as:



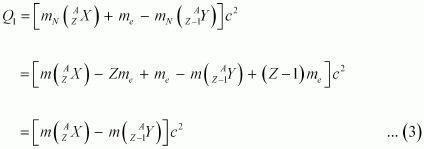
    Q-value of the positron capture reaction is given as:



    It can be inferred that if Q2 > 0, then Q1 > 0; Also, if Q1> 0, it does not necessarily mean that Q2 > 0.

    In other words, this means that if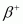emission is energetically allowed, then the electron capture process is necessarily allowed, but not vice-versa. This is because the Q-value must be positive for an energetically-allowed nuclear reaction.
  • Qstn #23
    In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are 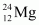(23.98504u),

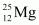    (24.98584u) and 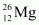(25.98259u). The natural abundance of 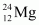is 78.99% by mass. Calculate the abundances of other two isotopes.
    Ans : Average atomic mass of magnesium, m = 24.312 u

    Mass of magnesium isotope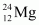, m1 = 23.98504 u

    Mass of magnesium isotope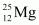, m2 = 24.98584 u

    Mass of magnesium isotope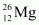, m3 = 25.98259 u

    Abundance of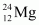, η1= 78.99%

    Abundance of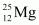, η2 = x%

    Hence, abundance of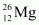, η3 = 100 - x - 78.99% = (21.01 - x)%

    We have the relation for the average atomic mass as:



    Hence, the abundance of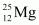 is 9.3% and that of 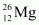is 11.71%.
next page