NEET-XII-Physics
13: Nuclei
- #5A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of
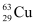atoms (of mass 62.92960 u).
Ans : Mass of a copper coin, m’ = 3 g
Atomic mass of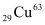
atom, m = 62.92960 u
The total number of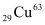atoms in the coin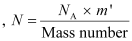
Where,
NA = Avogadro’s number = 6.023 × 1023 atoms /g
Mass number = 63 g
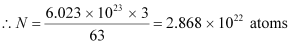
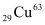nucleus has 29 protons and (63 - 29) 34 neutrons
∴Mass defect of this nucleus, Δm‘ = 29 × mH + 34 × mn - m
Where,
Mass of a proton, mH = 1.007825 u
Mass of a neutron, mn = 1.008665 u
∴Δm‘ = 29 × 1.007825 + 34 × 1.008665 - 62.9296
= 0.591935 u
Mass defect of all the atoms present in the coin, Δm = 0.591935 × 2.868 × 1022
= 1.69766958 × 1022 u
But 1 u = 931.5 MeV/c2
∴Δm = 1.69766958 × 1022 × 931.5 MeV/c2
Hence, the binding energy of the nuclei of the coin is given as:
Eb= Δmc2
= 1.69766958 × 1022 × 931.5.gif)
= 1.581 × 1025 MeV
But 1 MeV = 1.6 × 10-13 J
Eb = 1.581 × 1025 × 1.6 × 10-13
= 2.5296 × 1012 J
This much energy is required to separate all the neutrons and protons from the given coin.