NEET-XII-Physics
11: Gravitation
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #6Which of the following quantities remain constant in a planetary motion (consider elliptical orbits) as seen from the sun?
(a) Speed
(b) Angular speed
(c) Kinetic Energy
(d) Angular momentum.digAnsr: dAns : (d) Angular momentum.
In planetary motion, the net external torque on the planet is zero. Therefore, angular momentum will remain constant.
Page No 225:
- #Section : iv
- Qstn #1Two spherical balls of mass 10 kg each are placed 10 cm apart. Find the gravitational force of attraction between them.Ans : The gravitational force of attraction between the balls is given as by
`` F\mathit{=}\frac{G{m}_{\mathit{1}}{m}_{\mathit{2}}}{{r}^{\mathit{2}}}``
`` \,\mathrm{\,Given\,}:{m}_{1}={m}_{2}=10\,\mathrm{\,kg\,}\,\mathrm{\,and\,}r=10\,\mathrm{\,cm\,}=0.10\,\mathrm{\,m\,}``
`` \therefore F=\frac{6.67\times {10}^{-11}\times 10\times 10}{{\left(0.1\right)}^{2}}``
`` \Rightarrow F=6.67\times {10}^{-7}\,\mathrm{\,N\,}``
Page No 225:
- Qstn #2Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.Ans :
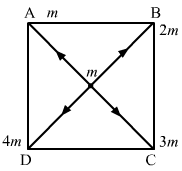
`` \,\mathrm{\,Force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,at\,}\,\mathrm{\,A\,},{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OA\,}}=\frac{\,\mathrm{\,G\,}\times m\times m}{{\,\mathrm{\,OA\,}}^{2}}``
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,OA\,}=r``
`` \therefore {\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OA\,}}=\frac{\,\mathrm{\,G\,}\times m\times m}{{r}^{2}}``
`` \,\mathrm{\,Here\,},r=\sqrt{{\left(\frac{a}{2}\right)}^{2}+{\left(\frac{a}{2}\right)}^{2}}=\frac{a}{\sqrt{2}}``
`` \,\mathrm{\,Force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,at\,}\,\mathrm{\,B\,},{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OB\,}}=\frac{\,\mathrm{\,G\,}\times m\times 2m}{{r}^{2}}``
`` \,\mathrm{\,Force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,at\,}\,\mathrm{\,C\,},{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OC\,}}=\frac{\,\mathrm{\,G\,}\times m\times 3m}{{r}^{2}}``
`` \,\mathrm{\,Force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,at\,}\,\mathrm{\,D\,},{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OD\,}}=\frac{\,\mathrm{\,G\,}\times m\times 4m}{{r}^{2}}``
`` \,\mathrm{\,Now\,},\,\mathrm{\,resultant\,}\,\mathrm{\,force\,}={\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OA\,}}+{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OB\,}}+{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OC\,}}+{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OD\,}}``
`` =\frac{2\,\mathrm{\,G\,}mm}{{a}^{2}}\left[-\frac{\stackrel{\to }{i}}{\sqrt{2}}+\frac{\stackrel{\to }{j}}{\sqrt{2}}\right]+\frac{4\,\mathrm{\,G\,}mm}{{a}^{2}}\left[\frac{\stackrel{\to }{i}}{\sqrt{2}}+\frac{\stackrel{\to }{j}}{\sqrt{2}}\right]``
`` =\frac{6\,\mathrm{\,G\,}mm}{{a}^{2}}\left[\frac{\stackrel{\to }{i}}{\sqrt{2}}-\frac{\stackrel{\to }{j}}{\sqrt{2}}\right]+\frac{8\,\mathrm{\,G\,}mm}{{a}^{2}}\left[\frac{-\stackrel{\to }{i}}{\sqrt{2}}-\frac{-\stackrel{\to }{j}}{\sqrt{2}}\right]``
Page No 226:
- Qstn #3Three equal masses m are placed at the three corners of an equilateral triangle of side a. Find the force exerted by this system on another particle of mass m placed at
- #3-athe mid-point of a side,Ans : Consider that mass 'm' is placed at the midpoint O of side AB of equilateral triangle ABC.
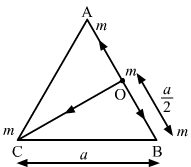
AO = BO = `` \frac{a}{2}``
Then `` {\stackrel{\to }{F}}_{\,\mathrm{\,OA\,}}=\frac{4\,\mathrm{\,G\,}{m}^{2}}{{a}^{2}}`` along OA
Also, `` {\stackrel{\to }{F}}_{\,\mathrm{\,OB\,}}=\frac{4\,\mathrm{\,G\,}{m}^{2}}{{a}^{2}}`` along OB
OC = `` \frac{\sqrt{3}a}{2}``
`` {\stackrel{\to }{F}}_{\,\mathrm{\,OC\,}}=\frac{4\,\mathrm{\,G\,}{m}^{2}}{\left\{\left(3\right){a}^{2}\right\}}=\frac{4G{m}^{2}}{3{a}^{2}}`` along OC
The net force on the particle at O is `` \stackrel{\to }{F}={\stackrel{\to }{F}}_{\,\mathrm{\,OA\,}}+{\stackrel{\to }{F}}_{\,\mathrm{\,OB\,}}+{\stackrel{\to }{F}}_{\,\mathrm{\,OC\,}}``.
Since equal and opposite forces cancel each other, we have:
`` \stackrel{\to }{F}={\stackrel{\to }{F}}_{\,\mathrm{\,OC\,}}=\frac{4\,\mathrm{\,G\,}{m}^{2}}{\left\{\left(3\right){a}^{2}\right\}}=\frac{4G{m}^{2}}{3{a}^{2}}`` along OC.
- #3-bat the centre of the triangle.Ans : If the particle placed at O (centroid)
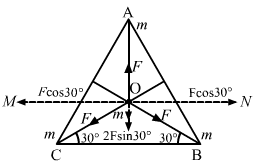
All the forces are equal in magnitude but their directions are different as shown in the figure.
Equal and opposite forces along OM and ON cancel each other.
i.e., `` F\,\mathrm{\,cos\,}30°=F\,\mathrm{\,cos\,}30°``
∴ Resultant force `` =F-2F\,\mathrm{\,sin\,}30=0``
Page No 226:
- Qstn #4Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.Ans : Three spheres are placed with their centres at A, B and C as shown in the figure.
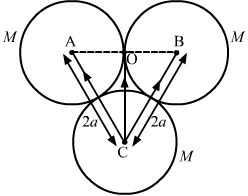
Gravitational force on sphere C due to sphere B is given by
`` {\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CB\,}}=\frac{\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}\,\mathrm{\,cos\,}60°\stackrel{‸}{i}+\frac{\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}·\,\mathrm{\,sin\,}60°\stackrel{‸}{j}``
Gravitational force on sphere C due to sphere A is given by
`` {\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CA\,}}=-\frac{\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}\,\mathrm{\,cos\,}60°\stackrel{‸}{i}+\frac{\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}·\,\mathrm{\,sin\,}60°\stackrel{‸}{j}``
`` \therefore {\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CB\,}}={\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CB\,}}+{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CA\,}}``
`` =+\frac{2\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}\,\mathrm{\,sin\,}60°\stackrel{‸}{j}``
`` =+\frac{2\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}\times \frac{\sqrt{3}}{2}``
i.e., magnitude`` =\frac{\sqrt{3}\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}`` along CO
Page No 226:
- Qstn #5Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.Ans : Assume that three particles are at points A, B and C on the circumference of a circle.
BC = CD = `` \sqrt{2}a``
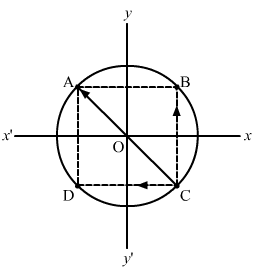
The force on the particle at C due to gravitational attraction of the particle at B is `` {\stackrel{\to }{F}}_{\,\mathrm{\,CB\,}}=\frac{\,\mathrm{\,G\,}{M}^{2}}{2{\,\mathrm{\,R\,}}^{2}}\stackrel{‸}{j}``.
The force on the particle at C due to gravitational attraction of the particle at D is `` {\stackrel{\to }{F}}_{\,\mathrm{\,CD\,}}=-\frac{G{M}^{2}}{2{\,\mathrm{\,R\,}}^{2}}\stackrel{‸}{i}``.
Now, force on the particle at C due to gravitational attraction of the particle at A is given by
`` {\stackrel{\to }{F}}_{\,\mathrm{\,CA\,}}=-\frac{\,\mathrm{\,G\,}{M}^{2}}{4{R}^{2}}\,\mathrm{\,cos\,}45\stackrel{‸}{i}+\frac{\,\mathrm{\,G\,}{M}^{2}}{4{R}^{2}}\,\mathrm{\,sin\,}45\stackrel{‸}{j}``
`` \therefore {\stackrel{\to }{F}}_{\,\mathrm{\,C\,}}={\stackrel{\to }{F}}_{\,\mathrm{\,CA\,}}+{\stackrel{\mathit{\to }}{F}}_{\,\mathrm{\,CB\,}}+{\stackrel{\mathit{\to }}{F}}_{\,\mathrm{\,CD\,}}``
`` =\frac{-\,\mathrm{\,G\,}{M}^{2}}{4{R}^{2}}\left(2+\frac{1}{\sqrt{2}}\right)\stackrel{‸}{i}+\frac{\,\mathrm{\,G\,}{M}^{2}}{4{R}^{2}}\left(2+\frac{1}{\sqrt{2}}\right)\stackrel{‸}{j}``
So, the resultant gravitational force on C is `` {\,\mathrm{\,F\,}}_{\,\mathrm{\,C\,}}=\frac{\,\mathrm{\,G\,}{m}^{2}}{4{\,\mathrm{\,R\,}}^{2}}\sqrt{2\sqrt{2}+1}``.
Let v be the velocity with which the particle is moving.
Centripetal force on the particle is given by
`` F=\frac{m{v}^{2}}{R}``
`` \Rightarrow v\mathit{=}\sqrt{\frac{\mathit{G}\mathit{M}}{\mathit{R}}\left(\frac{\mathit{2}\sqrt{\mathit{2}}\mathit{+}\mathit{1}}{\mathit{4}}\right)}``
Page No 226:
- Qstn #6Find the acceleration due to gravity of the moon at a point 1000 km above the moon’s surface. The mass of the moon is 7.4 × 1022 kg and its radius is 1740 km.Ans : The acceleration due to gravity at a point at height h from the surface of the moon is given by
`` g=\frac{\,\mathrm{\,G\,}M}{{r}^{2}}``,
where M is the mass of the moon; r is the distance of point from the centre of the moon and G is universal gravitational constant.
`` \therefore g=\frac{GM}{{\left(R\mathit{+}h\right)}^{2}}``
`` \Rightarrow g=\frac{6.67\times {10}^{-11}\times 7.4\times {10}^{22}}{{\left(1740+1000\right)}^{2}\times {10}^{6}}``
`` \Rightarrow g=\frac{6.67\times 7.4\times {10}^{11}}{\left(1740+{1000}^{2}\times {10}^{6}\right)}``
`` \Rightarrow g=\frac{6.67\times 7.4\times {10}^{11}}{2740\times 2740\times {10}^{6}}``
`` \Rightarrow g=0.65\,\mathrm{\,m\,}/{\,\mathrm{\,s\,}}^{2}``
Page No 226:
- Qstn #7Two small bodies of masses 10 kg and 20 kg are kept a distance 1.0 m apart and released. Assuming that only mutual gravitational forces are acting, find the speeds of the particles when the separation decreases to 0.5 m.Ans : Consider a system of two bodies. The initial linear momentum of the system is zero as the bodies were initially at rest when they were released.
Since the gravitational force is an internal force and the net external force on the system is zero, so by the law of conservation of linear momentum, the final momentum of the system will also be zero.
So, 10`` \times ``v1 = 20`` \times ``v2
⇒ v1 = 2v2 ...(i)
Applying the law of conservation of energy, we have:
Initial total energy = final total energy ...(ii)
Initial total energy`` =\frac{-6.67\times {10}^{11}\times 10\times 20}{1}`` + 0
= -13.34 × 10-9 J ...(iii)
When the separation is 0.5 m, we have:
Final total energy `` =\frac{-13.34\times {10}^{-9}}{1/2}+\left(\frac{1}{2}\right)\times 10{v}_{1}^{2}+\left(\frac{1}{2}\right)\times 20{v}_{2}^{2}...\left(iv\right)``
From (iii) and (iv), we have:
-13.34 × 10-9 = 26.68 × 10-9 + `` 5{v}_{1}^{2}+10{v}_{2}^{2}``
⇒-13.34 × 10-9 = 26.68 + 10-9 + `` 30{v}_{2}^{2}``
`` \Rightarrow {v}_{2}^{2}=\frac{-13.34\times {10}^{-9}}{30}`` = 4.44 × 10-10
⇒ v2 = 2.1 × 10-5 m/s
∴ v1 = 4.2 × 10-5 m/s
Page No 226:
- Qstn #8A semicircular wire has a length L and mass M. A particle of mass m is placed at the centre of the circle. Find the gravitational attraction on the particle due to the wire.Ans : Consider a small mass element of length dl subtending dθ angle at the centre.
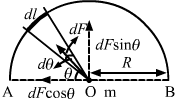
In the semicircle, we can consider a small element dθ.
Then length of the element, dl = R dθ
Mass of the element, dm `` =\left(\frac{\mathit{M}}{\mathit{L}}\right)Rd\,\mathrm{\,\theta \,}``
Force on the mass element is given by
`` d\,\mathrm{\,F\,}=\frac{\,\mathrm{\,G\,}m}{{R}^{2}}dm=\frac{GMRm}{L{R}^{2}}d\theta ``
The symmetric components along AB cancel each other.
Now, net gravitational force on the particle at O is given by
`` F=\int 2dF\,\mathrm{\,sin\,}\,\mathrm{\,\theta \,}``
`` =\int \frac{2GMm}{LR}\,\mathrm{\,sin\,}\,\mathrm{\,\theta \,}d\,\mathrm{\,\theta \,}``
`` \therefore F={\int }_{0}^{\,\mathrm{\,\pi \,}/2}\frac{-2\,\mathrm{\,G\,}Mm}{LR}\,\mathrm{\,sin\,}\,\mathrm{\,\theta \,}d\,\mathrm{\,\theta \,}``
`` =\frac{2\,\mathrm{\,G\,}Mm}{LR}{\left[-\,\mathrm{\,cos\,}\,\mathrm{\,\theta \,}\right]}_{0}^{\,\mathrm{\,\pi \,}/2}``
`` =-2\frac{\,\mathrm{\,G\,}Mm}{LR}\left(-1\right)``
`` =\frac{2\,\mathrm{\,G\,}Mm}{LR}=\frac{2\,\mathrm{\,G\,}Mm}{LL/\,\mathrm{\,\pi \,}}``
`` =\frac{2\,\mathrm{\,\pi G\,}Mm}{{L}^{2}}``
Page No 226:
- Qstn #9Derive an expression for the gravitational field due to a uniform rod of length L and mass M at a point on its perpendicular bisector at a distance d from the centre.Ans : Consider a small mass element of length dx at a distance x from the centre of the rod.
Mass of the mass element, dm = (M/L) × dx
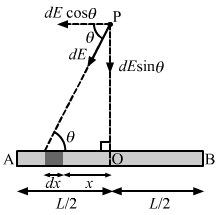
Gravitational field due to this element at point P is given by
`` dE=\frac{\,\mathrm{\,G\,}\left(dm\right)\times 1}{\left({d}^{2}+{x}^{2}\right)}``
The components of the gravitational field due to the symmetrical mass element along the length of the rod cancel each other.
Now, resultant gravitational field = 2dE sin θ
`` =2\times \frac{\,\mathrm{\,G\,}\left(dm\right)}{\left({d}^{2}+{x}^{2}\right)}\times \frac{d}{\sqrt{\left({d}^{2}+{x}^{2}\right)}}``
`` =\frac{2\times GM\times ddx}{L\left({d}^{2}+{x}^{2}\right)\left\{\left(\sqrt{{d}^{2}+{x}^{2}}\right)\right\}}``
Total gravitational field due to the rod at point P is given by
`` E={\int }_{0}^{\,\mathrm{\,L\,}/2}\frac{2Gmddx}{L{\left({d}^{2}+{x}^{2}\right)}^{3/2}}``.
On integrating the above equation, we get:
`` \,\mathrm{\,E\,}=\frac{2\,\mathrm{\,G\,}m}{d\sqrt{{L}^{2}+4{d}^{2}}}``
Page No 226:
- Qstn #10Two concentric spherical shells have masses M1, M2 and radii R1, R2 (R1 < R2). What is the force exerted by this system on a particle of mass m1 if it is placed at a distance (R1 + R2)/2 from the centre?Ans : Consider that mass m is at a distance `` \frac{{R}_{1}+{R}_{2}}{2}`` as shown in the figure.
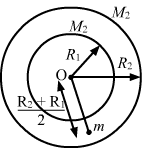
The gravitational force of m due to the shell of M2 is zero, because the mass is inside the shell.
∴ Gravitational force due to the shell of mass M2 = `` \frac{G{M}_{1}m}{{\left({\displaystyle \frac{{R}_{1}+{R}_{2}}{2}}\right)}^{2}}=\frac{4G{M}_{1}m}{{\left({R}_{1}+{R}_{2}\right)}^{2}}``
Page No 226:
- Qstn #11A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.Ans : Mass of the Earth, `` M=\left(\frac{4}{3}\right)\pi {R}^{3}\,\mathrm{\,\rho \,}`` ...(i)
Consider an imaginary sphere of radius x with centre O as shown in the figure below:
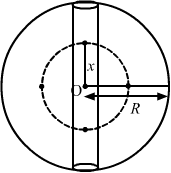
`` \,\mathrm{\,Mass\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,imaginary\,}\,\mathrm{\,sphere\,},M\text{'}=\left(\frac{4}{3}\right)\,\mathrm{\,\pi \,}{\textcolor[rgb]{0.09803921568627451,0.09803921568627451,0.09803921568627451}{\,\mathrm{\,x\,}}}^{3}\,\mathrm{\,\rho \,}...\left(ii\right)``
`` \,\mathrm{\,From\,}\left(i\right)\,\mathrm{\,and\,}\left(ii\right),\,\mathrm{\,we\,}\,\mathrm{\,have\,}:``
`` \frac{M\mathit{\text{'}}}{M}=\frac{{x}^{3}}{{R}^{3}}``
∴ Gravitational force on the particle of mass m is given by
F`` =\frac{GMm}{{x}^{2}}``
`` \Rightarrow F=\frac{GM{x}^{3}m}{{R}^{3}{x}^{2}}=\frac{GMm}{{R}^{3}}x``
Page No 226: