NEET-XII-Physics
11: Gravitation
- #5Four particles of equal masses M move along a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.Ans : Assume that three particles are at points A, B and C on the circumference of a circle.
BC = CD = `` \sqrt{2}a``
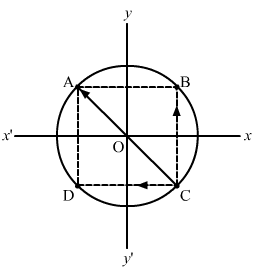
The force on the particle at C due to gravitational attraction of the particle at B is `` {\stackrel{\to }{F}}_{\,\mathrm{\,CB\,}}=\frac{\,\mathrm{\,G\,}{M}^{2}}{2{\,\mathrm{\,R\,}}^{2}}\stackrel{‸}{j}``.
The force on the particle at C due to gravitational attraction of the particle at D is `` {\stackrel{\to }{F}}_{\,\mathrm{\,CD\,}}=-\frac{G{M}^{2}}{2{\,\mathrm{\,R\,}}^{2}}\stackrel{‸}{i}``.
Now, force on the particle at C due to gravitational attraction of the particle at A is given by
`` {\stackrel{\to }{F}}_{\,\mathrm{\,CA\,}}=-\frac{\,\mathrm{\,G\,}{M}^{2}}{4{R}^{2}}\,\mathrm{\,cos\,}45\stackrel{‸}{i}+\frac{\,\mathrm{\,G\,}{M}^{2}}{4{R}^{2}}\,\mathrm{\,sin\,}45\stackrel{‸}{j}``
`` \therefore {\stackrel{\to }{F}}_{\,\mathrm{\,C\,}}={\stackrel{\to }{F}}_{\,\mathrm{\,CA\,}}+{\stackrel{\mathit{\to }}{F}}_{\,\mathrm{\,CB\,}}+{\stackrel{\mathit{\to }}{F}}_{\,\mathrm{\,CD\,}}``
`` =\frac{-\,\mathrm{\,G\,}{M}^{2}}{4{R}^{2}}\left(2+\frac{1}{\sqrt{2}}\right)\stackrel{‸}{i}+\frac{\,\mathrm{\,G\,}{M}^{2}}{4{R}^{2}}\left(2+\frac{1}{\sqrt{2}}\right)\stackrel{‸}{j}``
So, the resultant gravitational force on C is `` {\,\mathrm{\,F\,}}_{\,\mathrm{\,C\,}}=\frac{\,\mathrm{\,G\,}{m}^{2}}{4{\,\mathrm{\,R\,}}^{2}}\sqrt{2\sqrt{2}+1}``.
Let v be the velocity with which the particle is moving.
Centripetal force on the particle is given by
`` F=\frac{m{v}^{2}}{R}``
`` \Rightarrow v\mathit{=}\sqrt{\frac{\mathit{G}\mathit{M}}{\mathit{R}}\left(\frac{\mathit{2}\sqrt{\mathit{2}}\mathit{+}\mathit{1}}{\mathit{4}}\right)}``
Page No 226: