NEET-XII-Physics
11: Gravitation
- #4Three uniform spheres each having a mass M and radius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.Ans : Three spheres are placed with their centres at A, B and C as shown in the figure.
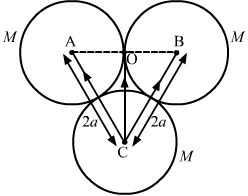
Gravitational force on sphere C due to sphere B is given by
`` {\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CB\,}}=\frac{\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}\,\mathrm{\,cos\,}60°\stackrel{‸}{i}+\frac{\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}·\,\mathrm{\,sin\,}60°\stackrel{‸}{j}``
Gravitational force on sphere C due to sphere A is given by
`` {\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CA\,}}=-\frac{\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}\,\mathrm{\,cos\,}60°\stackrel{‸}{i}+\frac{\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}·\,\mathrm{\,sin\,}60°\stackrel{‸}{j}``
`` \therefore {\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CB\,}}={\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CB\,}}+{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,CA\,}}``
`` =+\frac{2\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}\,\mathrm{\,sin\,}60°\stackrel{‸}{j}``
`` =+\frac{2\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}\times \frac{\sqrt{3}}{2}``
i.e., magnitude`` =\frac{\sqrt{3}\,\mathrm{\,G\,}{m}^{2}}{4{a}^{2}}`` along CO
Page No 226: