Qstnid -Iv-2-four Particles Having Masses M, 2m, 3m And 4m Are Placed At The Four Corners Of A Square Of Edge A. Find The Gravitational Force Acting On A Particle Of Mass M Placed At The Centre. - 11: Gravitation

Home Learn Fast select Course

Show Unit/Chapter Change Unit Change Subject Last Menu

NEET-XII-Physics

11: Gravitation

with Solutions - page 4

Qstn# iv-2 Prvs-Qstn Next-Qstn

#2
Four particles having masses m, 2m, 3m and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
Ans :
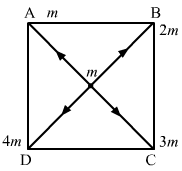
`` \,\mathrm{\,Force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,at\,}\,\mathrm{\,A\,},{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OA\,}}=\frac{\,\mathrm{\,G\,}\times m\times m}{{\,\mathrm{\,OA\,}}^{2}}``
`` \,\mathrm{\,Suppose\,}\,\mathrm{\,OA\,}=r``
`` \therefore {\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OA\,}}=\frac{\,\mathrm{\,G\,}\times m\times m}{{r}^{2}}``
`` \,\mathrm{\,Here\,},r=\sqrt{{\left(\frac{a}{2}\right)}^{2}+{\left(\frac{a}{2}\right)}^{2}}=\frac{a}{\sqrt{2}}``
`` \,\mathrm{\,Force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,at\,}\,\mathrm{\,B\,},{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OB\,}}=\frac{\,\mathrm{\,G\,}\times m\times 2m}{{r}^{2}}``
`` \,\mathrm{\,Force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,at\,}\,\mathrm{\,C\,},{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OC\,}}=\frac{\,\mathrm{\,G\,}\times m\times 3m}{{r}^{2}}``
`` \,\mathrm{\,Force\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,particle\,}\,\mathrm{\,at\,}\,\mathrm{\,D\,},{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OD\,}}=\frac{\,\mathrm{\,G\,}\times m\times 4m}{{r}^{2}}``
`` \,\mathrm{\,Now\,},\,\mathrm{\,resultant\,}\,\mathrm{\,force\,}={\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OA\,}}+{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OB\,}}+{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OC\,}}+{\stackrel{\to }{\,\mathrm{\,F\,}}}_{\,\mathrm{\,OD\,}}``
`` =\frac{2\,\mathrm{\,G\,}mm}{{a}^{2}}\left[-\frac{\stackrel{\to }{i}}{\sqrt{2}}+\frac{\stackrel{\to }{j}}{\sqrt{2}}\right]+\frac{4\,\mathrm{\,G\,}mm}{{a}^{2}}\left[\frac{\stackrel{\to }{i}}{\sqrt{2}}+\frac{\stackrel{\to }{j}}{\sqrt{2}}\right]``
`` =\frac{6\,\mathrm{\,G\,}mm}{{a}^{2}}\left[\frac{\stackrel{\to }{i}}{\sqrt{2}}-\frac{\stackrel{\to }{j}}{\sqrt{2}}\right]+\frac{8\,\mathrm{\,G\,}mm}{{a}^{2}}\left[\frac{-\stackrel{\to }{i}}{\sqrt{2}}-\frac{-\stackrel{\to }{j}}{\sqrt{2}}\right]``
Page No 226: