Loading…
NEET-XII-Physics
11: Gravitation
- #11A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.Ans : Mass of the Earth, `` M=\left(\frac{4}{3}\right)\pi {R}^{3}\,\mathrm{\,\rho \,}`` ...(i)
Consider an imaginary sphere of radius x with centre O as shown in the figure below:
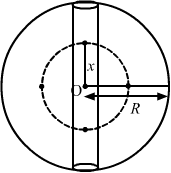
`` \,\mathrm{\,Mass\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,imaginary\,}\,\mathrm{\,sphere\,},M\text{'}=\left(\frac{4}{3}\right)\,\mathrm{\,\pi \,}{\textcolor[rgb]{0.09803921568627451,0.09803921568627451,0.09803921568627451}{\,\mathrm{\,x\,}}}^{3}\,\mathrm{\,\rho \,}...\left(ii\right)``
`` \,\mathrm{\,From\,}\left(i\right)\,\mathrm{\,and\,}\left(ii\right),\,\mathrm{\,we\,}\,\mathrm{\,have\,}:``
`` \frac{M\mathit{\text{'}}}{M}=\frac{{x}^{3}}{{R}^{3}}``
∴ Gravitational force on the particle of mass m is given by
F`` =\frac{GMm}{{x}^{2}}``
`` \Rightarrow F=\frac{GM{x}^{3}m}{{R}^{3}{x}^{2}}=\frac{GMm}{{R}^{3}}x``
Page No 226: