HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Chemistry

02: Solutions

with Solutions -

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • #
    Section : A
    Page No 37:
  • Qstn #1
    Calculate
    the mass percentage of benzene (C6H6)
    and carbon tetrachloride (CCl4)
    if 22 g of benzene is dissolved in 122 g of carbon tetrachloride.
    Ans : Mass
    percentage of C6H6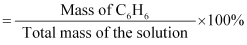

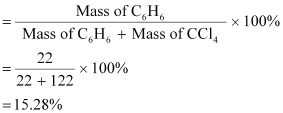
    Mass
    percentage of CCl4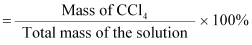

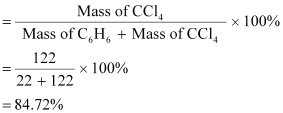
    Alternatively,
    Mass
    percentage of CCl4 = (100 - 15.28)%
    = 84.72%
  • Qstn #2
    Calculate
    the mole fraction of benzene in solution containing 30% by mass in
    carbon tetrachloride.
    Ans : Let
    the total mass of the solution be 100 g and the mass of benzene be 30
    g.
    ∴Mass
    of carbon tetrachloride = (100 - 30)g
    =
    70 g
    Molar
    mass of benzene (C6H6)
    = (6 × 12 + 6 × 1) g mol-1
    = 78
    g mol-1
    ∴Number
    of moles of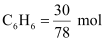
    = 0.3846 mol
    Molar
    mass of carbon tetrachloride (CCl4)
    = 1 × 12 + 4 × 355
    =
    154 g mol-1
    ∴Number
    of moles of CCl4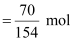
    = 0.4545 mol
    Thus,
    the mole fraction of C6H6 is given as:


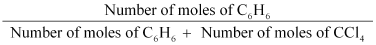
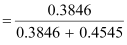
    = 0.458
  • Qstn #3
    Calculate
    the molarity of each of the following solutions:
    Ans : Molarity
    is given by:

  • #3-a
    30 g of Co(NO3)2.6H2O in 4 .3 L of solution
    Ans : Molar
    mass of Co (NO3)2.6H2O
    = 59 + 2 (14 + 3 × 16) + 6 × 18
    = 291 g mol-1
    ∴Moles
    of Co (NO3)2.6H2O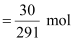
    = 0.103 mol
    Therefore,
    molarity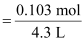
    = 0.023 M
  • #3-b
    30 mL of 0.5 M H2SO4 diluted to 500 mL.
    Ans : Number of moles present in 1000 mL of 0.5 M H2SO4 = 0.5 mol
    ∴Number
    of moles present in 30 mL of 0.5 M H2SO4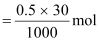
    = 0.015 mol
    Therefore, molarity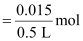
    = 0.03 M
  • Qstn #4
    Calculate the mass of urea (NH2CONH2)
    required in making 2.5 kg of 0.25 molal aqueous solution.
    Ans : Molar
    mass of urea (NH2CONH2)
    = 2(1 × 14 + 2 × 1) + 1 × 12 + 1 × 16
    = 60
    g mol-1
    0.25
    molar aqueous solution of urea means:
    1000 g of
    water contains 0.25 mol = (0.25 × 60)g of urea
    = 15 g of
    urea
    That is,
    (1000
    + 15) g of solution contains 15 g of urea
    Therefore,
    2.5 kg (2500 g) of solution contains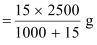
    = 36.95 g
    =
    37 g of urea (approximately)
    Hence,
    mass of urea required = 37 g
    Note: There is a slight variation in this answer and the one given in the
    NCERT textbook.
  • #5-a
    molality
    Ans : Molar
    mass of KI = 39 + 127 = 166 g mol-1
    20%
    (mass/mass) aqueous solution of KI means 20
    g of KI is present in 100 g of solution.
    That is,
    20
    g of KI is present in (100 - 20) g of
    water = 80 g of water
    Therefore,
    molality of the solution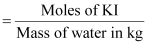

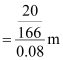
    = 1.506 m
    =
    1.51 m (approximately)
  • #5-b
    molarity and
    Ans : It
    is given that the density of the solution = 1.202 g mL-1
    ∴Volume
    of 100 g solution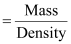

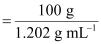
    = 83.19 mL
    =
    83.19 × 10-3 L
    Therefore,
    molarity of the solution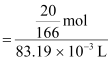
    = 1.45 M
  • #5-c
    mole fraction of KI if the density of 20% (mass/mass) aqueous KI is
    1.202 g mL-1.
    Ans : Moles
    of KI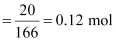
    Moles
    of water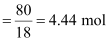
    Therefore,
    mole fraction of KI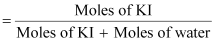

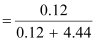
    = 0.0263
    Page No 41:
  • Qstn #6
    H2S,
    a toxic gas with rotten egg like smell, is used for the qualitative
    analysis. If the solubility of H2S
    in water at STP is 0.195 m, calculate Henry’s law constant.
    Ans : It
    is given that the solubility of H2S
    in water at STP is 0.195 m, i.e., 0.195 mol of H2S
    is dissolved in 1000 g of water.
    Moles
    of water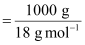
    = 55.56
    mol
    ∴Mole
    fraction of H2S, x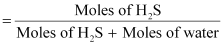

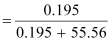
    = 0.0035
    At
    STP, pressure (p)
    = 0.987 bar
    According
    to Henry’s law:
    p = KHx

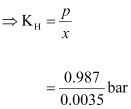
    = 282
    bar
  • Qstn #7
    Henry’s
    law constant for CO2 in water is 1.67 × 108 Pa at 298 K. Calculate the quantity of CO2 in 500 mL of soda water when packed under 2.5 atm CO2 pressure at 298 K.
    Ans : It
    is given that:
    KH = 1.67 × 108 Pa
    = 2.5 atm = 2.5 × 1.01325 × 105 Pa
    =
    2.533125 × 105 Pa
    According
    to Henry’s law:

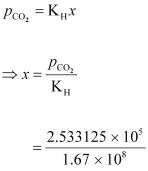
    = 0.00152
    We
    can write,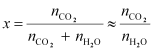
    [Since, is
    negligible as compared to]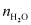
    In
    500 mL of soda water, the volume of water =
    500 mL
    [Neglecting
    the amount of soda present]
    We can
    write:
    500 mL of
    water = 500 g of water

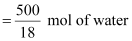
    = 27.78 mol of water
    Now,


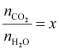
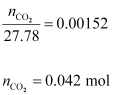
    Hence,
    quantity of CO2 in 500 mL of soda water = (0.042 × 44)g
    = 1.848 g
    Page No 47:
  • Qstn #8
    The
    vapour pressure of pure liquids A and B are 450 and 700 mm Hg
    respectively, at 350 K. Find out the composition of the liquid
    mixture if total vapour pressure is 600 mm Hg. Also find the
    composition of the vapour phase.
    Ans : It is
    given that:
    =
    450 mm of Hg
    =
    700 mm of Hg
    ptotal = 600 mm of Hg
    From
    Raoult’s law, we have:

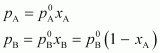
    Therefore,
    total pressure,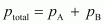

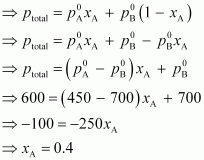
    Therefore,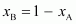
    = 1 -
    0.4
    = 0.6
    Now,

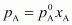
    = 450 ×
    0.4
    = 180 mm
    of Hg

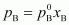
    = 700 ×
    0.6
    = 420 mm
    of Hg
    Now, in
    the vapour phase:
    Mole
    fraction of liquid A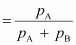

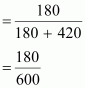
    = 0.30
    And,
    mole fraction of liquid B = 1 - 0.30
    =
    0.70
    Page No 55:
next page