NEET-XII-Physics
10: Rotational Mechanics
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #14A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.Ans :
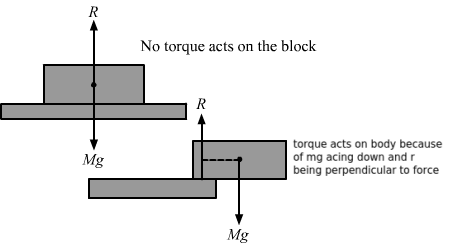
`` \,\mathrm{\,The\,}\,\mathrm{\,centre\,}\,\mathrm{\,of\,}\,\mathrm{\,mass\,}\left(\,\mathrm{\,CM\,}\right)\,\mathrm{\,of\,}\,\mathrm{\,a\,}\,\mathrm{\,rectangular\,}\,\mathrm{\,block\,}\,\mathrm{\,lies\,}\,\mathrm{\,in\,}\,\mathrm{\,the\,}\,\mathrm{\,middle\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,block\,}.\,\mathrm{\,When\,}\,\mathrm{\,the\,}\,\mathrm{\,block\,}\,\mathrm{\,is\,}\,\mathrm{\,projected\,}\,\mathrm{\,less\,}\,\mathrm{\,than\,}\,\mathrm{\,half\,}\,\mathrm{\,of\,}\,\mathrm{\,its\,}\,\mathrm{\,length\,}(\,\mathrm{\,CM\,}\,\mathrm{\,being\,}\,\mathrm{\,over\,}\,\mathrm{\,the\,}\,\mathrm{\,table\,}),\,\mathrm{\,no\,}\,\mathrm{\,net\,}\,\mathrm{\,force\,}\,\mathrm{\,acts\,}\,\mathrm{\,on\,}\,\mathrm{\,it\,}.\,\mathrm{\,Thus\,},\,\mathrm{\,no\,}\,\mathrm{\,net\,}\,\mathrm{\,torque\,}\,\mathrm{\,acts\,}\,\mathrm{\,upon\,}\,\mathrm{\,the\,}\,\mathrm{\,body\,}.\,\mathrm{\,But\,}\,\mathrm{\,if\,}\,\mathrm{\,the\,}\,\mathrm{\,block\,}\,\mathrm{\,is\,}``
`` \,\mathrm{\,projected\,}\,\mathrm{\,more\,}\,\mathrm{\,than\,}\,\mathrm{\,half\,}\,\mathrm{\,of\,}\,\mathrm{\,its\,}\,\mathrm{\,length\,}\,\mathrm{\,outside\,}\,\mathrm{\,the\,}\,\mathrm{\,table\,}(\,\mathrm{\,CM\,}\,\mathrm{\,being\,}\,\mathrm{\,outside\,}\,\mathrm{\,the\,}\,\mathrm{\,table\,}),\,\mathrm{\,gravitational\,}\,\mathrm{\,force\,}\,\mathrm{\,acts\,}\,\mathrm{\,along\,}\,\mathrm{\,the\,}\,\mathrm{\,CM\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,block\,}.\,\mathrm{\,This\,}\,\mathrm{\,force\,}\,\mathrm{\,produces\,}\,\mathrm{\,a\,}\,\mathrm{\,moment\,}\,\mathrm{\,along\,}\,\mathrm{\,the\,}\,\mathrm{\,edge\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,table\,}.\,\mathrm{\,This\,}\,\mathrm{\,rotates\,}\,\mathrm{\,the\,}\,\mathrm{\,block\,},\,\mathrm{\,and\,}\,\mathrm{\,as\,}\,\mathrm{\,a\,}\,\mathrm{\,result\,},\,\mathrm{\,it\,}\,\mathrm{\,falls\,}\,\mathrm{\,down\,}.``
Page No 192:
- Qstn #15When a fat person tries to touch his toes, keeping the legs straight, he generally falls. Explain with reference to figure (10-Q2).
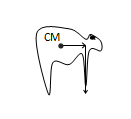
Figure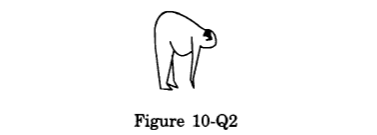
Ans : `` \,\mathrm{\,When\,}\,\mathrm{\,the\,}\,\mathrm{\,man\,}\,\mathrm{\,tries\,}\,\mathrm{\,to\,}\,\mathrm{\,touch\,}\,\mathrm{\,his\,}\,\mathrm{\,toe\,},\,\mathrm{\,he\,}\,\mathrm{\,exerts\,}\,\mathrm{\,force\,}\,\mathrm{\,along\,}\,\mathrm{\,the\,}\,\mathrm{\,hand\,}\,\mathrm{\,downwards\,}.\,\mathrm{\,This\,}\,\mathrm{\,force\,}\,\mathrm{\,produces\,}\,\mathrm{\,a\,}``
`` \,\mathrm{\,moment\,}\,\mathrm{\,along\,}\,\mathrm{\,the\,}\,\mathrm{\,Centre\,}\,\mathrm{\,of\,}\,\mathrm{\,Mass\,}\left(\,\mathrm{\,CM\,}\right)\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,man\,}\,\mathrm{\,as\,}\,\mathrm{\,shown\,}\,\mathrm{\,in\,}\,\mathrm{\,the\,}\,\mathrm{\,figure\,}.\,\mathrm{\,This\,}\,\mathrm{\,moment\,}\,\mathrm{\,makes\,}\,\mathrm{\,him\,}\,\mathrm{\,rotate\,}``
`` \,\mathrm{\,and\,},\,\mathrm{\,thus\,},\,\mathrm{\,he\,}\,\mathrm{\,falls\,}\,\mathrm{\,down\,}\,\mathrm{\,after\,}\,\mathrm{\,losing\,}\,\mathrm{\,the\,}\,\mathrm{\,balance\,}.``
Page No 192:
- Qstn #16A ladder is resting with one end on a vertical wall and the other end on a horizontal floor. If it more likely to slip when a man stands near the bottom or near the top?Ans : `` \,\mathrm{\,The\,}\,\mathrm{\,ladder\,}\,\mathrm{\,is\,}\,\mathrm{\,more\,}\,\mathrm{\,likely\,}\,\mathrm{\,to\,}\,\mathrm{\,slide\,}\,\mathrm{\,when\,}\,\mathrm{\,the\,}\,\mathrm{\,man\,}\,\mathrm{\,stands\,}\,\mathrm{\,near\,}\,\mathrm{\,the\,}\,\mathrm{\,top\,}.\,\mathrm{\,This\,}\,\mathrm{\,is\,}\,\mathrm{\,because\,}\,\mathrm{\,when\,}\,\mathrm{\,the\,}\,\mathrm{\,man\,}\,\mathrm{\,stands\,}\,\mathrm{\,near\,}\,\mathrm{\,the\,}\,\mathrm{\,top\,},\,\mathrm{\,it\,}\,\mathrm{\,creates\,}\,\mathrm{\,more\,}\,\mathrm{\,torque\,}``
`` \,\mathrm{\,compared\,}\,\mathrm{\,to\,}\,\mathrm{\,the\,}\,\mathrm{\,torque\,}\,\mathrm{\,caused\,}\,\mathrm{\,by\,}\,\mathrm{\,the\,}\,\mathrm{\,weight\,}\,\mathrm{\,of\,}\,\mathrm{\,man\,}\,\mathrm{\,near\,}\,\mathrm{\,the\,}\,\mathrm{\,bottom\,}.``
`` \,\mathrm{\,When\,}\,\mathrm{\,the\,}\,\mathrm{\,man\,}\,\mathrm{\,stands\,}\,\mathrm{\,near\,}\,\mathrm{\,the\,}\,\mathrm{\,bottom\,},\,\mathrm{\,the\,}\,\mathrm{\,Centre\,}\,\mathrm{\,of\,}\,\mathrm{\,Gravity\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,ladder\,}\,\mathrm{\,is\,}\,\mathrm{\,shifted\,}\,\mathrm{\,to\,}C\mathit{\text{'}}\,\mathrm{\,from\,}C.\,\mathrm{\,Now\,},\,\mathrm{\,the\,}\,\mathrm{\,couple\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,forces\,}\left(m+M\right)g\,\mathrm{\,and\,}N\,\mathrm{\,makes\,}``
`` \,\mathrm{\,the\,}\,\mathrm{\,ladder\,}\,\mathrm{\,fall\,}.\,\mathrm{\,We\,}\,\mathrm{\,see\,}\,\mathrm{\,that\,}\,\mathrm{\,due\,}\,\mathrm{\,to\,}\,\mathrm{\,its\,}\,\mathrm{\,shift\,}\,\mathrm{\,from\,}C\,\mathrm{\,to\,}C\mathit{\text{'}}\mathit{,}\,\mathrm{\,the\,}\,\mathrm{\,moment\,}\,\mathrm{\,arm\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,couple\,}\,\mathrm{\,decreases\,}\,\mathrm{\,from\,}r\,\mathrm{\,to\,}r\text{'};\,\mathrm{\,hence\,},\,\mathrm{\,the\,}\,\mathrm{\,couple\,}\,\mathrm{\,decreases\,}.``
`` ``
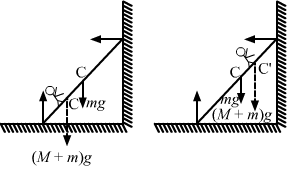
`` \,\mathrm{\,When\,}\,\mathrm{\,the\,}\,\mathrm{\,man\,}\,\mathrm{\,stands\,}\,\mathrm{\,near\,}\,\mathrm{\,the\,}\,\mathrm{\,top\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,ladder\,},\,\mathrm{\,the\,}\,\mathrm{\,Centre\,}\,\mathrm{\,of\,}\,\mathrm{\,Mass\,}\,\mathrm{\,shifts\,}\,\mathrm{\,from\,}C\,\mathrm{\,to\,}C\mathit{\text{'}}\mathit{.}\,\mathrm{\,This\,}\,\mathrm{\,increases\,}\,\mathrm{\,the\,}\,\mathrm{\,moment\,}\,\mathrm{\,arm\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,couple\,}\,\mathrm{\,and\,}\,\mathrm{\,from\,}r\,\mathrm{\,to\,}r\text{'}.``
`` \,\mathrm{\,Increase\,}\,\mathrm{\,in\,}\,\mathrm{\,moment\,}\,\mathrm{\,arm\,}\,\mathrm{\,increases\,}\,\mathrm{\,the\,}\,\mathrm{\,couple\,}\,\mathrm{\,and\,},\,\mathrm{\,thus\,},\,\mathrm{\,the\,}\,\mathrm{\,ladder\,}\,\mathrm{\,easily\,}\,\mathrm{\,falls\,}.``
Page No 192:
- Qstn #17When a body is weighed on an ordinary balance we demand that the arum should be horizontal if the weights on the two pans are equal. Suppose equal weights are put on the two pans, the arm is kept at an angle with the horizontal and released. Is the torque of the two weights about the middle point (point of support) zero? Is the total torque zero? If so, why does the arm rotate and finally become horizontal?Ans : When the balance is kept at an angle, there is a net extra torque given to one of its arm. When the extra torque is removed, the balance becomes torque free and sum of all the torque acting on it is zero.
But balance kept at an angle has got a greater potential energy compared to the balance kept horizontal. The potential energy acquired is due to the initial torque applied on it. This displaces the balance by an angle. As soon as the body is set free to rotate, the body tends to have the lowest potential energy. Thus, potential energy starts converting in to kinetic energy, but on the other side, kinetic energy converts into potential energy when the other arm of the balance is raised. This energy transformation oscillates the balance. But in this process, friction with the air and fulcrum dissipates energy converting into heat. Finally, the balance loses the energy and becomes horizontal, or attains equilibrium.
Page No 192:
- Qstn #18The density of a rod AB continuously increases from A to B. Is it easier to set it in rotation by clamping it at A and applying a perpendicular force at B or by clamping it at B and applying the force at A?Ans : It will require more force to set the bar into rotation by clamping at A and then clamping at B.
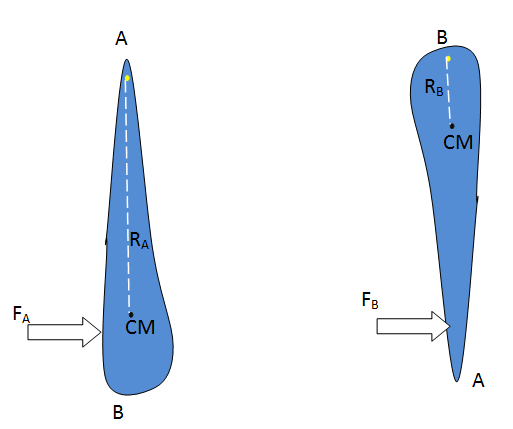
Explanation: Since the rod has mass density increasing towards B, the Center of Mass (CM) of the rod is near B. If the rod is clamped along A, the distance of CM of the rod from the pivot will be greater when the rod is clamped along B. Greater distance of CM from the Center of rotation increases the moment of inertia of the rod and hence more torque will be necessary to rotate the bar about A. Greater torque implies greater force will be necessary to rotate it.
FA = Force required to rotated the rod clamped at A
RA= Distance of CM from pivot A
M = Mass of the rod
FB = Force required to rotate the rod clamped at B
RB= Distance of CM from pivot B
We have RA>RB.
We have to find the torque required to rotate rod clamped at A to produce angular acceleration a.
TA = MRA2a = RAFA
=> FA = MRAa
We have to find torque required to rotate rod clamped at B to produce angular acceleration a.
TB = MRB2a = RBFB
=> FB = MRBa
On comparing, since RA>RB, we get:
FA>FB
Page No 192:
- Qstn #19When tall building are constructed on earth, the duration of day-night slightly increases. Is it true?Ans : Yes, because tall buildings have their CM much above the ground. It increases moment of inertia of the Earth. As the Earth’s rotation does not involve torque, its angular momentum is constant. Thus, an increase in MI leads to lower angular velocity of the Earth about its axis of rotation. This means length of night and day will increase. However, the increase is very small.
Page No 192:
- Qstn #20If the ice at the poles melts and flows towards the equator, how will it affect the duration of day-night?Ans : Ice caps near the poles concentrate the mass of water at the poles through which axis of rotation of the Earth passes. If the ice melts, water will spread across the globe due to hydrostatic equilibrium and tend to move to the equatorial areas of the Earth due to centrifugal force of rotation. Mass, now being distributed more along the equator, will increase MI of the Earth and this in turn will decrease the angular velocity of the Earth. Decrease in angular velocity will increase the duration of day-night.
Page No 192:
- Qstn #21A hollow sphere, a solid sphere, a disc and a ring all having same mass and radius are rolled down on an inclined plane. If no slipping takes place, which one will take the smallest time to cover a given length?Ans : The body with the smallest moment of inertia will roll down taking the smallest time. Here, the solid sphere has the lowest moment of inertia among all the other bodies. So, it will roll down taking the least time.
Page No 192:
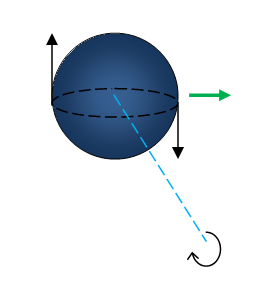
- Qstn #22A sphere rolls on a horizontal surface. If there any point of the sphere which has a vertical velocity?Ans : Some points on the equator of the sphere has got vertical velocity with respect to the direction of motion of the sphere.
Page No 193:
- #Section : ii
- Qstn #1Let
→Abe a unit vector along the axis of rotation of a purely rotating body and
→Bbe a unit vector along the velocity of a particle P of the body away from the axis. The value of
→A. →Bis
(a) 1
(b) -1
(c) 0
(d) None of these.digAnsr: cAns : (c) 0
For a purely rotating body, the axis of rotation is always perpendicular to the velocity of the particle.
Therefore, we have:
`` \stackrel{\to }{A}.\stackrel{\to }{B}=0``
Page No 193:
- Qstn #2A body is uniformly rotating about an axis fixed in an inertial frame of reference. Let
→Abe a unit vector along the axis of rotation and
→Bbe the unit vector along the resultant force on a particle P of the body away from the axis. The value of
→A . →Bis
(a) 1
(b) -1
(c) 0
(d) none of these.digAnsr: cAns : (c) 0
The unit vector along the axis of rotation and the unit vector along the resultant force on the particle are perpendicular to each other in a uniform rotation.
Therefore, we have:
`` \stackrel{\to }{A}.\stackrel{\to }{B}=0``
Page No 193:
- Qstn #3A particle moves with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
(a) is zero
(b) remains constant
(c) goes on increasing
(d) goes on decreasing.digAnsr: bAns : (b) remains constant
For angular momentum, we have:
`` \stackrel{\to }{L}=m\left(\stackrel{\to }{r}\times \stackrel{\to }{v}\right)``
`` \stackrel{\to }{v}=v\stackrel{‸}{i}\,\mathrm{\,and\,}\stackrel{\mathit{\to }}{r}=x\stackrel{\mathit{^}}{i}\mathit{+}y\stackrel{\mathit{^}}{j}``
`` \,\mathrm{\,So\,}\mathit{,}\stackrel{\mathit{\to }}{L}\mathit{=}\mathit{-}mvy\stackrel{\mathit{^}}{k}``
m, v and y are constant; therefore, angular momentum remains constant.
Page No 193:
- Qstn #4A body is in pure rotation. The linear speed
νof a particle, the distance r of the particle from the axis and the angular velocity
ωof the body are related as
ω=νr. Thus
(a)
ω=νr
(b)
ω∝r
(c)
ω=0
(d)
ωis independent of r.digAnsr: dAns : (d) `` \omega `` is independent of r
In a pure rotation, angular velocity of all the particles remains same and does not depend on the position of the particle from the axis of rotation.
Page No 193:
- Qstn #5Figure (10-Q3) shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distance travelled by A and B in the same time interval, then
(a) x = 2 y
(b) x = y
(c) y = 2 x
(d) none of these.
Figure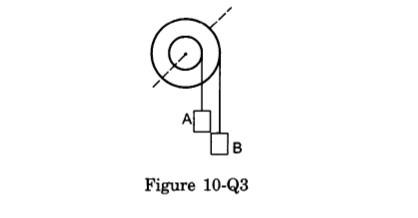
digAnsr: cAns : (c) y = 2 x
It is given that angular velocity is same for both the wheels.
Therefore, we have:
vA = `` \omega ``R
vB = `` \omega ``2R
x = vAt = `` \omega ``Rt ... (i)
y = vBt = `` \omega ``(2R)t ... (ii)
From equations (i) and (ii), we get:
y = 2 x
Page No 193: