NEET-XII-Physics
10: Rotational Mechanics
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #6A body is rotating uniformly about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
(a) vertical
(b) horizontal and skew with the axis
(c) horizontal and intersecting the axis
(d) none of these.digAnsr: cAns : (c) horizontal and intersecting the axis
Because resultant force on a particle of the body rotating uniformly is always perpendicular to the rotation axis and pass through it.
Page No 193:
- Qstn #7A body is rotating nonuniformity about a vertical axis fixed in an inertial frame. The resultant force on a particle of the body not on the axis is
(a) vertical
(b) horizontal and skew with the axis
(c) horizontal and intersecting the axis
(d) none of these.digAnsr: bAns : (b) horizontal and skew with the axis
The resultant force on a particle of the body rotating non-uniformly is always horizontal and skew with the rotation axis because net torque on the body is non-zero.
Page No 193:
- Qstn #8Let
→Fbe a force acting on a particle having position vector
→r. Let
→Γbe the torque of this force about the origin, then
(a)
r→.Γ→=0 and F→.Γ→=0
(b)
r→.Γ→=0 but F→.Γ→≠0
(c)
r→.Γ→≠0 but F→.Γ→=0
(d)
r→.Γ→≠0 and F→.Γ→≠0digAnsr: aAns : (a) `` \stackrel{\to }{r}.\stackrel{\to }{\,\mathrm{\,\Gamma \,}}=0\,\mathrm{\,and\,}\stackrel{\to }{F}.\stackrel{\to }{\,\mathrm{\,\Gamma \,}}=0``
We have:
`` \stackrel{\to }{\tau }=\stackrel{\to }{r}\times \stackrel{\to }{F}``
Thus, `` \stackrel{\to }{\,\mathrm{\,\tau \,}}`` is perpendicular to `` \stackrel{\to }{r}`` and `` \stackrel{\to }{F}``.
Therefore, we have:
`` \stackrel{\to }{r}.\stackrel{\to }{\,\mathrm{\,\tau \,}}=0\,\mathrm{\,and\,}\stackrel{\to }{F}.\stackrel{\to }{\,\mathrm{\,\tau \,}}=0``
Page No 193:
- Qstn #9One end of a uniform rod of mass m and length l is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity
ω. The force exerted by the clamp on the rod has a horizontal component
(a)
mω2l
(b) zero
(c) mg
(d)
12mω2t.digAnsr: dAns : (d) `` \frac{1}{2}m{\omega }^{2}l``.
Consider a small portion of rod at a distance x from the clamped end (as shown in fig.) with width dx and mass dm.
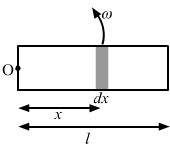
Centripetal force on this portion =`` {\omega }^{2}xdm``
`` dm=\left(\frac{m}{l}\right)ldx``
Force on the whole rod = F =`` {\int }_{0}^{l}{\omega }^{2}x\frac{m}{l}dx``
`` \therefore `` F = `` \frac{1}{2}m{\omega }^{2}l``
Page No 193:
- Qstn #10A uniform rod is kept vertically on a horizontal smooth surface at a point O. If it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain
(a) at O
(b) at a distance less than l/2 from O
(c) at a distance l/2 from O
(d) at a distance larger than l/2 from O.digAnsr: cAns : (c) at a distance l/2 from O.
It is given that there is no force along x-axis.
COM of rod will remain and will not shift along x-axis (horizontal direction).
Force gravity is acting along y-axis (vertical direction). So, COM will shift along the y-axis by l/2 distance and COM of horizontal rod is at a distance l/2 from one end. Therefore, lower end of the rod will remain at a distance l/2 from O.
Page No 193:
- Qstn #11A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IA and IB is
(a) IA > IB
(b) IA = IB
(c) IA < IB
(d) depends on the actual values of t and r.digAnsr: cAns : (c) IA < IB
Moment of inertia of circular disc of radius r:
I = `` \frac{1}{2}m{r}^{2}``
Mass = Volume × Density
Volume of disc = `` \,\mathrm{\,\pi \,}{r}^{2}t``
Here, t is the thickness of the disc.
As density is same for both the rods, we have:
Moment of inertia, `` I\propto \,\mathrm{\,thickness\,}\times {\left(\,\mathrm{\,radius\,}\right)}^{4}``
`` \frac{{I}_{A}}{{I}_{B}}=\frac{t.{\left(r\right)}^{4}}{{\displaystyle \frac{t}{4}}{\left(4r\right)}^{4}}<1``
`` \Rightarrow \frac{{I}_{A}}{{I}_{B}}<1``
`` \Rightarrow {I}_{\,\mathrm{\,A\,}}<{I}_{\,\mathrm{\,B\,}}``
Page No 193:
- Qstn #12Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are
νAand
νBrespectively. We have
(a)
νA > νB
(b)
νA = νB
(c)
νA < νB
(d) the relation depends on the actual magnitude of the torques.digAnsr: aAns : (a) `` {\nu }_{A}>{\nu }_{B}``
`` \tau =I\alpha \left(\,\mathrm{\,magnitude\,}\right)``
`` ``
For equal torque, we have:
`` {I}_{A}{\alpha }_{A}={I}_{B}{\alpha }_{B}``
IA < IB
⇒ `` {\alpha }_{A}>{\alpha }_{B}`` ...(i)
Now, `` \omega =\alpha t``
Or, `` \frac{v}{r}=\alpha t``
`` {\nu }_{A}>{\nu }_{B}`` (using (i))
Page No 193:
- Qstn #13A closed cylindrical tube containing some water (not filling the entire tube) lies in a horizontal plane. If the tube is rotated about a perpendicular bisector, the moment of inertia of water about the axis
(a) increases
(b) decreases
(c) remains constant
(d) increases if the rotation is clockwise and decreases if it is anticlockwise.digAnsr: aAns : (a) increases
Moment of inertia of a mass is directly proportional to the square of the distance of mass from the axis of rotation.
Therefore, we have:
`` I\propto {r}^{2}``

As the tube is rotated, water is collected at the end of tube because of centrifugal force and distance from the rotation axis increases. Hence, moment of inertia increases.
Page No 193:
- Qstn #14The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is
(a)
Mr2
(b)
12Mr2
(c)
14Mr2
(d)
25Mr2.digAnsr: aAns : (a) `` M{r}^{2}``
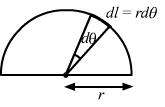
Consider an element of length, dl = rdθ.
`` dm=\frac{M}{\,\mathrm{\,\pi \,}r}dl=\frac{M}{\,\mathrm{\,\pi \,}r}rd\theta ``
MOI of semicircular wire = `` {\int }_{0}^{\,\mathrm{\,\pi \,}}{r}^{2}dm``
`` I={\int }_{0}^{\,\mathrm{\,\pi \,}}{r}^{2}\frac{m}{\,\mathrm{\,\pi \,}r}rd\theta ``
`` \Rightarrow I=m{r}^{2}``
Page No 193:
- Qstn #15Let I1 an I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminium and the second of iron.
(a) I1 < I2
(b) I1 = I2
(c) I1 > I2
(d) relation between I1 and I2 depends on the actual shapes of the bodies.digAnsr: aAns : (a) I1 < I2
In the given case, we have:
MOI `` \propto `` Density
The density of iron is more; therefore, I2 will be greater.
Page No 193:
- Qstn #16A body having its centre of mass at the origin has three of its particles at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0⋅20 kg-m2 each. The moment of inertia about the Z-axis
(a) is 0⋅20 kg-m2
(b) is 0⋅40 kg-m2
(c) is
0·202kg-m2
(d) cannot be deduced with this information.digAnsr: dAns : (d) cannot be deduced with this information.
Ix = m2a2 + m3a2 = 0.20 ...(i)
Iy = m1a2 + m3a2 = 0.20 ...(ii)
Iz = m1a2 + m2a2 ...(iii)
We have three equations and four variables. So, Iz cannot be deduced with the given information.
Page No 193:
- Qstn #17A cubical block of mass M and edge a slides down a rough inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has a magnitude
(a) zero
(b) Mga
(c) Mga sinθ
(d)
12 Mga sinθ.digAnsr: dAns : (d) `` \frac{1}{2}Mga\,\mathrm{\,sin\theta \,}``
Let N be the normal reaction on the block.
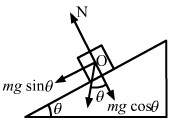
From the free body diagram of the block, it is clear that the forces N and mgcosθ pass through the same line. Therefore, there will be no torque due to N and mgcosθ. The only torque will be produced by mgsinθ.
`` \therefore \stackrel{\to }{\tau }=\stackrel{\to }{F}\times \stackrel{\to }{r}``
`` \,\mathrm{\,Since\,}a\,\mathrm{\,is\,}\,\mathrm{\,the\,}\,\mathrm{\,edge\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,cube\,},r=\frac{a}{2}.``
`` \,\mathrm{\,Thus\,},\,\mathrm{\,we\,}\,\mathrm{\,have\,}:``
`` \tau =mg\,\mathrm{\,sin\,}\theta \times \frac{a}{2}``
`` =\frac{1}{2}mga\,\mathrm{\,sin\,}\theta ``
Page No 194:
- Qstn #18A thin circular ring of mass M and radius r is rotating about its axis with an angular speed ω. Two particles having mass m each are now attached at diametrically opposite points. The angular speed of the ring will become
(a)
ωMM+m
(b)
ωMM+2 m
(c)
ωM-2 mM+2 m
(d)
ωM+2 mM.digAnsr: bAns : (b) `` \frac{\omega M}{M+2m}``
No external torque is applied on the ring; therefore, the angular momentum will be conserved.
`` I\omega =I\text{'}\omega \text{'}``
`` \Rightarrow \omega \text{'}=\frac{I\omega }{I\text{'}}...\left(i\right)``
`` I=M{r}^{2}``
`` I\text{'}=M{r}^{2}+2m{r}^{2}``
On putting these values in equation (i), we get:
`` \omega \text{'}=\frac{\omega M}{M+2m}``
Page No 194:
- Qstn #19A person sitting firmly over a rotating stool has his arms stretched. If he folds his arms, his angular momentum about the axis of rotation
(a) increases
(b) decreases
(c) remains unchanged
(d) doubles.digAnsr: cAns : (c) remains unchanged
Rate of change of angular momentum of the body is directly proportional to the net external torque acting on the body.
No external torque is applied on the person or on the table; therefore, the angular momentum will be conserved.
Page No 194:
- Qstn #20The centre of a wheel rolling on a plane surface moves with a speed
ν0. A particle on the rim of the wheel at the same level as the centre will be moving at speed
(a) zero
(b)
ν0
(c)
2ν0
(d)
2ν0.digAnsr: cAns : (c) `` \sqrt{2}{\nu }_{0}``
For pure rolling, `` \omega r={v}_{0}``
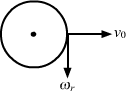
As shown in the figure, the velocity of the particle will be the resultant of v0 and ωr.
Therefore, we have:
`` {v}_{net}=\sqrt{{{v}_{0}}^{2}+{\left(\omega r\right)}^{2}}``
`` {v}_{net}=\sqrt{{{v}_{0}}^{2}+{{v}_{0}}^{2}}``
`` {v}_{net}=\sqrt{2}{v}_{0}``
Page No 194: