NEET-XII-Physics
07: Circular Motion
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #18A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?Ans : Given:
Speed of vehicles = v = 36 km/hr = 10 m/s
Radius = r = 20 m
Coefficient of static friction = μ = 0.4
Let the road be banked with an angle `` \theta ``. We have:
`` \theta ={\,\mathrm{\,tan \,}}^{-1}\frac{{v}^{2}}{rg}``
`` ={\,\mathrm{\,tan \,}}^{-1}\frac{100}{20\times 10}``
`` ={\,\mathrm{\,tan \,}}^{-1}\left(\frac{1}{2}\right)``
`` \Rightarrow \,\mathrm{\,tan\theta \,}=0.5``
When the car travels at the maximum speed, it slips upward and μN1 acts downward.
Therefore we have:
`` {N}_{1}-mg\,\mathrm{\,cos \,}\theta -\frac{m{v}_{1}^{2}}{r}\,\mathrm{\,sin \,}\theta =0...\left(\,\mathrm{\,i \,}\right)``
`` \mu {N}_{1}+mg\,\mathrm{\,sin \,}\theta \mathit{-}\frac{m{v}_{\mathit{1}}^{\mathit{2}}}{r}\,\mathrm{\,cos \,}\theta =0...\left(\,\mathrm{\,ii \,}\right)``
On solving the above equations, we get:
`` {v}_{1}=\sqrt{rg\frac{\mu +\,\mathrm{\,tan \,}\theta }{1-\mu \,\mathrm{\,tan \,}\theta }}``
`` =\sqrt{20\times 10\times \frac{0.9}{0.8}}``
`` =15\,\mathrm{\,m \,}/\,\mathrm{\,s \,}=54\,\mathrm{\,km \,}/\,\mathrm{\,hr \,}``
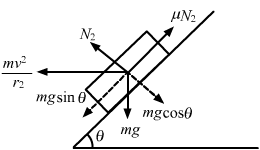
Similarly, for the other case, it can be proved that:
`` {v}_{2}=\sqrt{rg\frac{\,\mathrm{\,tan\theta \,}-\,\mathrm{\,\mu \,}}{\sqrt{1-\,\mathrm{\,\mu \,}\,\mathrm{\,tan\theta \,}}}}``
`` =\sqrt{20\times 10\times \frac{0.1}{1.2}}``
`` =4.08\,\mathrm{\,m \,}/\,\mathrm{\,s \,}=14.7\,\mathrm{\,km \,}/\,\mathrm{\,hr \,}``
Thus, the possible speeds are between 14.7 km/hr and 54 km/hr so that the car neither slips down nor skids up.
Page No 115:
- Qstn #19A motorcycle has to move with a constant speed on an over bridge which is in the form of a circular arc of radius R and has a total length L. Suppose the motorcycle starts from the highest point.Ans : R = Radius of the bridge
L = Total length of the over bridge
- #19-aWhat can its maximum velocity be for which the contact with the road is not broken at the highest point?Ans : At the highest point:
Let m be the mass of the motorcycle and v be the required velocity.
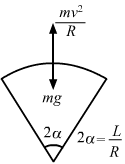
`` mg=\frac{m{v}^{2}}{R}``
`` \Rightarrow {v}^{2}=Rg``
`` \Rightarrow v=\sqrt{Rrg}``
`` ``
`` \left(\,\mathrm{\,b \,}\right)\,\mathrm{\,Given \,}:``
`` v=\left(\frac{1}{\sqrt{2}}\right)\sqrt{Rg}``
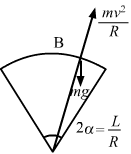
Suppose it loses contact at B.
`` \,\mathrm{\,At \,}\,\mathrm{\,point \,}\,\mathrm{\,B \,},\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` mg\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{R}``
`` \Rightarrow {v}^{2}=Rg\,\mathrm{\,cos \,}\theta ``
`` \,\mathrm{\,Putting \,}\,\mathrm{\,the \,}\,\mathrm{\,value \,}\,\mathrm{\,of \,}v,\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` \sqrt{{\left(\frac{Rg}{2}\right)}^{2}}=Rg\,\mathrm{\,cos \,}\theta ``
`` \Rightarrow \frac{Rg}{2}=Rg\,\mathrm{\,cos \,}\theta ``
`` \Rightarrow \,\mathrm{\,cos \,}\theta =\frac{1}{2}``
`` \Rightarrow \,\mathrm{\,\theta \,}=60°=\frac{\,\mathrm{\,\pi \,}}{3}``
`` \because \theta =\frac{L}{R}``
`` \therefore L=R\theta =\frac{\pi R}{3}``
So, it will lose contact at a distance `` \frac{\pi R}{3}`` from the highest point.
(c) Let the uniform speed on the bridge be v. The chances of losing contact is maximum at the end bridge. We have:
`` \alpha =\frac{L}{2R}``
`` \,\mathrm{\,So \,},\frac{m{v}^{2}}{R}=mg\,\mathrm{\,cos \,}\alpha ``
`` \Rightarrow v=\sqrt{g\,\mathrm{\,Rcos \,}\left(\frac{L}{2R}\right)}``
Page No 115:
- Qstn #20A car goes on a horizontal circular road of radius R, the speed increasing at a constant rate
dvdt=a. The friction coefficient between the road and the tyre is μ. Find the speed at which the car will skid.Ans : Let v be the speed of the car.
Since the motion is non-uniform, the acceleration has both radial (ar) and tangential (at) components.
`` {a}_{r}=\frac{{v}^{2}}{R}``
`` {a}_{t}=\frac{dv}{dt}=a``
`` \,\mathrm{\,Resultant \,}\,\mathrm{\,magnitude \,}=\sqrt{{\left(\frac{{v}^{2}}{R}\right)}^{2}+{a}^{2}}``
`` ``
`` ``
From free body diagram, we have:
`` mN=m\sqrt{{\left(\frac{{v}^{2}}{R}\right)}^{2}+{a}^{2}}``
`` \Rightarrow \mu mg=m\sqrt{{\left(\frac{{v}^{2}}{R}\right)}^{2}+{a}^{2}}``
`` \Rightarrow {\mu }^{2}{g}^{2}=\frac{{v}^{4}}{{R}^{2}}+{a}^{2}``
`` \Rightarrow \frac{{v}^{4}}{{R}^{2}}=({\,\mathrm{\,\mu \,}}^{2}{g}^{2}-{a}^{2})``
`` \Rightarrow {v}^{4}=({\,\mathrm{\,\mu \,}}^{2}{g}^{2}-{a}^{2}){R}^{2}``
`` \Rightarrow v=\left[\right({\,\mathrm{\,\mu \,}}^{2}{\,\mathrm{\,g \,}}^{2}-{\,\mathrm{\,a \,}}^{2}){R}^{2}{]}^{1/4}``
Page No 115:
- Qstn #21A block of mass m is kept on a horizontal ruler. The friction coefficient between the ruler and the block is μ. The ruler is fixed at one end and the block is at a distance L from the fixed end. The ruler is rotated about the fixed end in the horizontal plane through the fixed end.
- #21-aWhat can the maximum angular speed be for which the block does not slip?Ans : Given:
Mass of the block = m
Friction coefficient between the ruler and the block = μ
Let the maximum angular speed be ω1 for which the block does not slip
Now, for the uniform circular motion in the horizontal plane, we have:
`` \mu mg=m{{\omega }_{1}}^{2}L``
`` \therefore {\omega }_{1}=\sqrt{\frac{\mu g}{L}}``
- #21-bIf the angular speed of the ruler is uniformly increased from zero at an angular acceleration α, at what angular speed will the block slip?Ans : Let the block slip at an angular speed ω2.
For the uniformly accelerated circular motion, we have:
`` \mu mg=\sqrt{{\left(m{\omega }_{2}^{2}L\right)}^{2}+{\left(mL{\alpha }^{2}\right)}^{2}}``
`` \Rightarrow {\omega }_{2}^{4}+{\alpha }^{2}=\frac{{\mu }^{2}{g}^{2}}{{L}^{2}}``
`` \Rightarrow {\omega }_{2}={\left[{\left(\frac{\mu g}{L}\right)}^{2}-{\alpha }^{2}\right]}^{1/4}``
Page No 115:
- Qstn #22A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track.
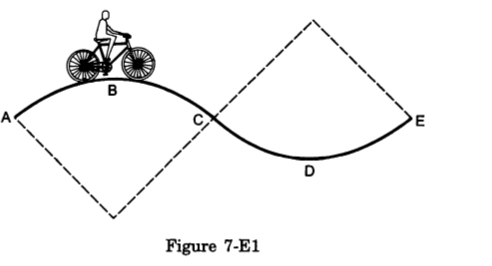Ans : Given:
Radius of the curves = r = 100 m
Mass of the cycle = m = 100 kg
Velocity = v = 18 km/hr = 5 m/s
`` \left(a\right)\,\mathrm{\,At \,}\,\mathrm{\,B \,},\,\mathrm{\,we \,}\,\mathrm{\,have \,}:``
`` mg-\frac{m{v}^{2}}{r}=N``
`` \Rightarrow N=(100\times 10)-\left(100\times \frac{25}{100}\right)``
`` =1000-25=975\,\mathrm{\,N \,}``
`` \,\mathrm{\,At \,}\,\mathrm{\,D \,},\,\mathrm{\,we \,}\,\mathrm{\,have \,}:``
`` N=mg+\frac{m{v}^{2}}{r}``
`` =1000+25=1025\,\mathrm{\,N \,}``
(b) At B and D, we have:
Tendency of the cycle to slide is zero.
So, at B and D, frictional force is zero.
At C, we have:
mgsinθ = f
`` \Rightarrow 1000\times \left(\frac{1}{\sqrt{2}}\right)=707\,\mathrm{\,N \,}``
`` \left(\,\mathrm{\,c \,}\right)\left(i\right)\,\mathrm{\,Before \,}\,\mathrm{\,C \,},``
`` mg\,\mathrm{\,cos \,}\theta -N=\frac{m{v}^{2}}{r}``
`` \Rightarrow N=mg\,\mathrm{\,cos \,}\theta -\frac{m{v}^{2}}{r}``
`` =707-25=682\,\mathrm{\,N \,}``
`` \left(ii\right)N-mg\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{r}``
`` \Rightarrow \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}+mg\,\mathrm{\,cos \,}\theta ``
`` =25+707=732\,\mathrm{\,N \,}``
(d) To find the minimum coefficient of friction, we have to consider a point where N is minimum or a point just before c .
`` \,\mathrm{\,Therefore \,},\,\mathrm{\,we \,}\,\mathrm{\,have \,}:``
`` \mu \,\mathrm{\,N \,}=mg\,\mathrm{\,sin \,}\theta ``
`` \Rightarrow \,\mathrm{\,\mu \,}\times 682=707``
`` \Rightarrow \,\mathrm{\,\mu \,}=1.037``
Page No 115:
- Qstn #23In a children’s park a heavy rod is pivoted at the centre and is made to rotate about the pivot so that the rod always remains horizontal. Two kids hold the rod near the ends and thus rotate with the rod. Let the mass of each kid be 15 kg, the distance between the points of the rod where the two kids hold it be 3.0 m and suppose that the rod rotates at the rate of 20 revolutions per minute. Find the force of friction exerted by the rod on one of the kids.
Figure
Ans : Given:
`` \,\mathrm{\,Frequency \,}\,\mathrm{\,of \,}\,\mathrm{\,rod \,}=n=20\,\mathrm{\,rev \,}\,\mathrm{\,per \,}\,\mathrm{\,min \,}``
`` \Rightarrow n=\frac{20}{60}=\frac{1}{3}\,\mathrm{\,rev \,}/\,\mathrm{\,s \,}``
`` ``
`` ``
Therefore, we have:
angular velocity of rod,
`` \,\mathrm{\,Angular \,}\,\mathrm{\,velocity \,}\,\mathrm{\,of \,}\,\mathrm{\,rod \,}=\omega =2\pi n=\frac{2\pi }{3}\,\mathrm{\,rad \,}/\,\mathrm{\,s \,}``
Mass of each kid = `` m=15\,\mathrm{\,kg \,}``
Radius = `` r=\frac{3}{2}=1.5\,\mathrm{\,m \,}``
`` \therefore \,\mathrm{\,Frictional \,}\,\mathrm{\,force \,}=F=mr{\,\mathrm{\,\omega \,}}^{2}``
`` \Rightarrow F=15\times (1.5)\times \frac{(2\,\mathrm{\,\pi \,}{)}^{2}}{9}``
`` =5\times (0.5)\times 4{\,\mathrm{\,\pi \,}}^{2}=10{\,\mathrm{\,\pi \,}}^{2}\,\mathrm{\,N \,}``
`` ``
Thus, the force of frictional on one of the kids is 10`` \pi ``2.
Page No 115:
- Qstn #24A hemispherical bowl of radius R is rotated about its axis of symmetry which is kept vertical. A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rotates with the bowl without any slipping. The friction coefficient between the block and the bowl surface is μ. Find the range of the angular speed for which the block will not slip.Ans : When the bowl rotates at maximum angular speed, the block tends to slip upwards.
Also, the frictional force acts downward.
Here, we have:
Radius of the path that the block follow = r = Rsinθ
Let N1 be the normal reaction on the block and ω1 be the angular velocity after which the block will slip.
From the free body diagram-1, we get:
`` {N}_{1}-mg\,\mathrm{\,cos \,}\theta ={\,\mathrm{\,m\omega \,}}_{1}^{2}\left(R\,\mathrm{\,sin \,}\theta \right)\,\mathrm{\,sin \,}\theta ...\left(\,\mathrm{\,i \,}\right)``
`` \mu {N}_{1}+mg\,\mathrm{\,sin\theta \,}=m{\,\mathrm{\,\omega \,}}_{1}^{2}\left(R\,\mathrm{\,sin \,}\theta \right)\,\mathrm{\,cos \,}\theta ...\left(\,\mathrm{\,ii \,}\right)``
`` ``
On solving the two equation, we get:
`` {\,\mathrm{\,\omega \,}}_{1}={\left[\frac{g(\,\mathrm{\,sin\theta \,}+\,\mathrm{\,\mu \,}\,\mathrm{\,cos\theta \,})}{R\,\mathrm{\,sin\theta \,}(\,\mathrm{\,cos\theta \,}-\,\mathrm{\,\mu \,}\,\mathrm{\,sin\theta \,})}\right]}^{1/2}``
Let us now find the minimum speed (ω2) on altering the direction of `` \mu `` (as shown in figure):
`` {\,\mathrm{\,\omega \,}}_{2}={\left[\frac{g(\,\mathrm{\,sin\theta \,}-\mu \,\mathrm{\,cos\theta \,})}{R\,\mathrm{\,sin\theta \,}(\,\mathrm{\,cos\theta \,}+\mu \,\mathrm{\,sin\theta \,})}\right]}^{1/2}``
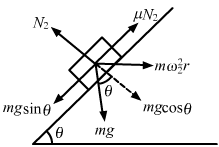
Hence, the range of speed is between ω2 and ω1.
Page No 115:
- Qstn #25A particle is projected with a speed u at an angle θ with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circular circle? This radius is called the radius of curvature of the curve at the point.Ans : At the highest point, the vertical component of velocity is zero.
So, at the highest point, we have:
velocity = v = ucosθ
Centripetal force on the particle = `` \frac{m{v}^{2}}{r}``
`` \Rightarrow \frac{m{v}^{2}}{r}=\frac{m{u}^{2}{\,\mathrm{\,cos \,}}^{2}\,\mathrm{\,\theta \,}}{r}``
At the highest point, we have:
`` mg=\frac{m{v}^{2}}{r}``
Here, r is the radius of curvature of the curve at the point.
`` \Rightarrow r=\frac{{u}^{2}{\,\mathrm{\,cos \,}}^{2}\theta }{g}``
Page No 115:
- Qstn #26What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?Ans : Let u be the initial velocity and v be the velocity at the point where it makes an angle `` \frac{\,\mathrm{\,\theta \,}}{2}``with the horizontal component.
It is given that the horizontal component remains unchanged.
Therefore, we get:
`` v\,\mathrm{\,cos \,}\left(\frac{\,\mathrm{\,\theta \,}}{2}\right)=u\,\mathrm{\,cos\theta \,}``
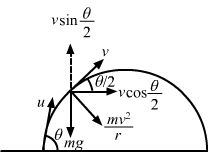
`` \Rightarrow v=\frac{u\,\mathrm{\,cos \,}\theta }{\,\mathrm{\,cos \,}{\displaystyle \frac{\theta }{2}}}...\left(\,\mathrm{\,i \,}\right)``
`` mg\,\mathrm{\,cos \,}\frac{\theta }{2}=\frac{m{v}^{2}}{r}...\left(\,\mathrm{\,ii \,}\right)``
`` \Rightarrow r=\frac{{v}^{2}}{g\,\mathrm{\,cos \,}{\displaystyle \frac{\theta }{2}}}``
On substituting the value of v from equation (i), we get:
`` r=\frac{{u}^{2}{\,\mathrm{\,cos \,}}^{2}\theta }{g{\,\mathrm{\,cos \,}}^{2}{\displaystyle \frac{\theta }{2}}}``
Page No 115:
- Qstn #27A block of mass m moves on a horizontal circle against the wall of a cylindrical room of radius R. The floor of the room on which the block moves is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v writeAns :
Given:
Radius of the room = R
Mass of the block = m
- #27-athe normal force by the wall on the block,Ans : Normal reaction by the wall on the block = N = `` \frac{m{v}^{2}}{R}``
- #27-bthe frictional force by wall andAns : Force of frictional by the wall = `` \mu N=\frac{\mu m{v}^{2}}{R}``