NEET-XII-Physics
07: Circular Motion
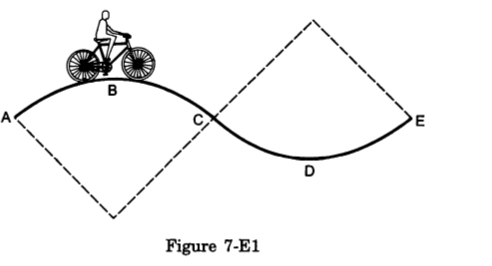
- #22A track consists of two circular parts ABC and CDE of equal radius 100 m and joined smoothly as shown in figure. Each part subtends a right angle at its centre. A cycle weighing 100 kg together with the rider travels at a constant speed of 18 km/h on the track.
 Ans : Given:
Ans : Given:
Radius of the curves = r = 100 m
Mass of the cycle = m = 100 kg
Velocity = v = 18 km/hr = 5 m/s
`` \left(a\right)\,\mathrm{\,At \,}\,\mathrm{\,B \,},\,\mathrm{\,we \,}\,\mathrm{\,have \,}:``
`` mg-\frac{m{v}^{2}}{r}=N``
`` \Rightarrow N=(100\times 10)-\left(100\times \frac{25}{100}\right)``
`` =1000-25=975\,\mathrm{\,N \,}``
`` \,\mathrm{\,At \,}\,\mathrm{\,D \,},\,\mathrm{\,we \,}\,\mathrm{\,have \,}:``
`` N=mg+\frac{m{v}^{2}}{r}``
`` =1000+25=1025\,\mathrm{\,N \,}``
(b) At B and D, we have:
Tendency of the cycle to slide is zero.
So, at B and D, frictional force is zero.
At C, we have:
mgsinθ = f
`` \Rightarrow 1000\times \left(\frac{1}{\sqrt{2}}\right)=707\,\mathrm{\,N \,}``
`` \left(\,\mathrm{\,c \,}\right)\left(i\right)\,\mathrm{\,Before \,}\,\mathrm{\,C \,},``
`` mg\,\mathrm{\,cos \,}\theta -N=\frac{m{v}^{2}}{r}``
`` \Rightarrow N=mg\,\mathrm{\,cos \,}\theta -\frac{m{v}^{2}}{r}``
`` =707-25=682\,\mathrm{\,N \,}``
`` \left(ii\right)N-mg\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{r}``
`` \Rightarrow \,\mathrm{\,N \,}=\frac{m{v}^{2}}{r}+mg\,\mathrm{\,cos \,}\theta ``
`` =25+707=732\,\mathrm{\,N \,}``
(d) To find the minimum coefficient of friction, we have to consider a point where N is minimum or a point just before c .
`` \,\mathrm{\,Therefore \,},\,\mathrm{\,we \,}\,\mathrm{\,have \,}:``
`` \mu \,\mathrm{\,N \,}=mg\,\mathrm{\,sin \,}\theta ``
`` \Rightarrow \,\mathrm{\,\mu \,}\times 682=707``
`` \Rightarrow \,\mathrm{\,\mu \,}=1.037``
Page No 115: