NEET-XII-Physics
07: Circular Motion
- #18A turn of radius 20 m is banked for the vehicles going at a speed of 36 km/h. If the coefficient of static friction between the road and the tyre is 0.4, what are the possible speeds of a vehicle so that it neither slips down nor skids up?Ans : Given:
Speed of vehicles = v = 36 km/hr = 10 m/s
Radius = r = 20 m
Coefficient of static friction = μ = 0.4
Let the road be banked with an angle `` \theta ``. We have:
`` \theta ={\,\mathrm{\,tan \,}}^{-1}\frac{{v}^{2}}{rg}``
`` ={\,\mathrm{\,tan \,}}^{-1}\frac{100}{20\times 10}``
`` ={\,\mathrm{\,tan \,}}^{-1}\left(\frac{1}{2}\right)``
`` \Rightarrow \,\mathrm{\,tan\theta \,}=0.5``

When the car travels at the maximum speed, it slips upward and μN1 acts downward.
Therefore we have:
`` {N}_{1}-mg\,\mathrm{\,cos \,}\theta -\frac{m{v}_{1}^{2}}{r}\,\mathrm{\,sin \,}\theta =0...\left(\,\mathrm{\,i \,}\right)``
`` \mu {N}_{1}+mg\,\mathrm{\,sin \,}\theta \mathit{-}\frac{m{v}_{\mathit{1}}^{\mathit{2}}}{r}\,\mathrm{\,cos \,}\theta =0...\left(\,\mathrm{\,ii \,}\right)``
On solving the above equations, we get:
`` {v}_{1}=\sqrt{rg\frac{\mu +\,\mathrm{\,tan \,}\theta }{1-\mu \,\mathrm{\,tan \,}\theta }}``
`` =\sqrt{20\times 10\times \frac{0.9}{0.8}}``
`` =15\,\mathrm{\,m \,}/\,\mathrm{\,s \,}=54\,\mathrm{\,km \,}/\,\mathrm{\,hr \,}``
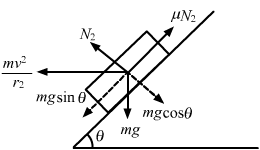
Similarly, for the other case, it can be proved that:
`` {v}_{2}=\sqrt{rg\frac{\,\mathrm{\,tan\theta \,}-\,\mathrm{\,\mu \,}}{\sqrt{1-\,\mathrm{\,\mu \,}\,\mathrm{\,tan\theta \,}}}}``
`` =\sqrt{20\times 10\times \frac{0.1}{1.2}}``
`` =4.08\,\mathrm{\,m \,}/\,\mathrm{\,s \,}=14.7\,\mathrm{\,km \,}/\,\mathrm{\,hr \,}``
Thus, the possible speeds are between 14.7 km/hr and 54 km/hr so that the car neither slips down nor skids up.
Page No 115: