NEET-XII-Physics
07: Circular Motion
- #26What is the radius of curvature of the parabola traced out by the projectile in the previous problem at a point where the particle velocity makes an angle θ/2 with the horizontal?Ans : Let u be the initial velocity and v be the velocity at the point where it makes an angle `` \frac{\,\mathrm{\,\theta \,}}{2}``with the horizontal component.
It is given that the horizontal component remains unchanged.
Therefore, we get:
`` v\,\mathrm{\,cos \,}\left(\frac{\,\mathrm{\,\theta \,}}{2}\right)=u\,\mathrm{\,cos\theta \,}``
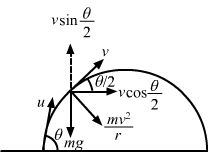
`` \Rightarrow v=\frac{u\,\mathrm{\,cos \,}\theta }{\,\mathrm{\,cos \,}{\displaystyle \frac{\theta }{2}}}...\left(\,\mathrm{\,i \,}\right)``
`` mg\,\mathrm{\,cos \,}\frac{\theta }{2}=\frac{m{v}^{2}}{r}...\left(\,\mathrm{\,ii \,}\right)``
`` \Rightarrow r=\frac{{v}^{2}}{g\,\mathrm{\,cos \,}{\displaystyle \frac{\theta }{2}}}``
On substituting the value of v from equation (i), we get:
`` r=\frac{{u}^{2}{\,\mathrm{\,cos \,}}^{2}\theta }{g{\,\mathrm{\,cos \,}}^{2}{\displaystyle \frac{\theta }{2}}}``
Page No 115: