31: Capacitors : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

31: Capacitors

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#
Section : iv

Qstn #1
When 1⋅0 × 10¹² electrons are transferred from one conductor to another, a potential difference of 10 V appears between the conductors. Calculate the capacitance of the two-conductor system.
Ans : As 1.0 × 10¹²electrons are transferred from one conductor to another, the conductor to which the electrons are transferred becomes negatively charged and the other conductor becomes positively charged.
Now,
Magnitude of the net charge on each conductor, Q = (1.0 × 10¹²) × (1.6 × 10^{`` -``19}) C = 1.6 × 10^{`` -``7} C
Magnitude of the potential difference between the conductors, V = 10 V
The capacitance C is the ratio of the magnitude of the charge on either conductor to the magnitude of the potential difference between the conductors.
`` C=\frac{Q}{V}``
`` \Rightarrow C=\frac{1.6\times {10}^{-7}}{10}=1.6\times {10}^{-8}\,\mathrm{\,F\,}``
Hence, the value of the capacitance of the given two conductor systems is 1.6 × 10^{`` -``8} F.
Page No 165:

Qstn #2
The plates of a parallel-plate capacitor are made of circular discs of radii 5⋅0 cm each. If the separation between the plates is 1⋅0 mm, what is the capacitance?
Ans : The capacitance of a parallel-plate capacitor is given by
`` C=\frac{{\in }_{0}A}{d}``
Here,
A = Area of the plate
d = Distance between the parallel plates
Given:
`` \,\mathrm{\,A\,}=\,\mathrm{\,\pi \,}{r}^{2}=\,\mathrm{\,\pi \,}\times {\left(5\times {10}^{-2}\right)}^{2}``
`` d=1.0\times {10}^{-3}\,\mathrm{\,m\,}``
`` {\in }_{0}=8.85\times {10}^{-12}\,\mathrm{\,F\,}/\,\mathrm{\,m\,}``
`` \therefore C=\frac{{\in }_{0}A}{d}``
`` =\frac{8.85\times {10}^{-12}\times 3.14\times 25\times {10}^{-4}}{{10}^{-3}}``
`` =6.95\times {10}^{-5}\,\mathrm{\,\mu F\,}``
Page No 165:

Qstn #3
Suppose, one wishes to construct a 1⋅0 farad capacitor using circular discs. If the separation between the discs be kept at 1⋅0 mm, what would be the radius of the discs?
Ans : The capacitance of a parallel-plate capacitor is given by
`` C=\frac{{\in }_{0}A}{d}``
Here,
A = Area of the plate
d = Distance between the parallel plates
Now,
Let the radius of the disc be r.
`` \therefore C=\frac{{\in }_{0}A}{d}=\frac{{\in }_{0}\left(\,\mathrm{\,\pi \,}{r}^{2}\right)}{d}``
`` \Rightarrow r=\sqrt{\frac{Cd}{{\in }_{0}\,\mathrm{\,\pi \,}}}``
`` \Rightarrow r=\sqrt{\frac{1\times (1\times {10}^{-3})}{8.85\times {10}^{-12}\times 3.14}}=\sqrt{35.98\times {10}^{6}}\,\mathrm{\,m\,}``
`` ``
`` \Rightarrow r\approx \sqrt{36\times {10}^{6}}\,\mathrm{\,m\,}=6\times {10}^{3}\,\mathrm{\,m\,}=6\,\mathrm{\,km\,}``
`` ``
Thus, the radius of the plates of the capacitor for the given configuration is 6 km.
Page No 165:

Qstn #4
A parallel-plate capacitor having plate area 25 cm² and separation 1⋅00 mm is connected to a battery of 6⋅0 V. Calculate the charge flown through the battery. How much work has been done by the battery during the process?
Ans : The capacitance of a parallel-plate capacitor is given by
`` C=\frac{{\in }_{0}A}{d}``
Here,
A = Area of the plate
d = Distance between the parallel plates
Given:
A = 25 cm² = 25 × 10^{`` -``4} m²
d = 1.00 mm = 1 × 10^{`` -``3} m
Now,
`` C=\frac{{\in }_{0}\,\mathrm{\,A\,}}{d}=\frac{8.85\times {10}^{-12}\times 25\times {10}^{-4}}{1\times {10}^{-3}}``
`` =2.21\times {10}^{-11}\,\mathrm{\,F\,}``
When the battery of voltage 6 V is connected to the capacitor, the charge (Q) that flows from the battery is equal to the amount of the charge that the given capacitor can hold.
`` \Rightarrow ``Q = CV
`` \Rightarrow Q=2.21\times {10}^{-11}\times 6.0``
`` =1.33\times {10}^{-10}\,\mathrm{\,C\,}``
The work done by the battery in charging the capacitor is calculated by taking the product of the magnitude of the charge transferred and the voltage of the battery.
Thus, we get
`` W=QV``
`` =1.33\times {10}^{-10}\times 6.0``
`` =8.0\times {10}^{-10}\,\mathrm{\,J\,}``
Thus, the charge flown through the battery is 1.33 × 10^{`` -``10} C and the work done by the battery is 8.0 × 10^{`` -``10}J.
Page No 165:

Qstn #5
A parallel-plate capacitor has plate area 25⋅0 cm² and a separation of 2⋅00 mm between the plates. The capacitor is connected to a battery of 12⋅0 V.
Ans : Given:
Area of the plate, A = 25 cm² = 25 × 10^{`` -``4} m²
Separation between the plates, d = 2 mm = 2 × 10^{`` -``3} m
Potential difference between the plates, V = 12 V
The capacitance of the given capacitor is given by
`` C=\frac{{\in }_{0}A}{d}``
`` =\frac{(8.85\times {10}^{-12})\times (25\times {10}^{-4})}{(2\times {10}^{-3})}``
`` =11.06\times {10}^{-12}\,\mathrm{\,F\,}``

#5-a
Find the charge on the capacitor.
Ans : Charge on the capacitor is given by
Q = CV
`` =11.06\times {10}^{-12}\times 12``
`` =1.33\times {10}^{-10}\,\mathrm{\,C\,}``

#5-b
The plate separation is decreased to 1⋅00 mm. Find the extra charge given by the battery to the positive plate.
Ans : When the separation between the plates is decreased to 1 mm, the capacitance C' can be calculated as:
`` C\text{'}=\frac{{\in }_{0}\,\mathrm{\,A\,}}{d}``
`` =\frac{(8.85\times {10}^{-12})\times (25\times {10}^{-4})}{1\times {10}^{-3}}``
`` =22.12\times {10}^{-12}\,\mathrm{\,F\,}``
`` ``
Charge on the capacitor is given by
Q' = C'V
`` =22.12\times {10}^{-12}\times 12``
`` =2.65\times {10}^{-10}\,\mathrm{\,C\,}``
`` \,\mathrm{\,Extra\,}\,\mathrm{\,charge\,}``
`` =\left(2.65\times {10}^{-10}-1.32\times {10}^{-10}\right)\,\mathrm{\,C\,}``
`` =1.33\times {10}^{-10}\,\mathrm{\,C\,}``
Page No 165:

Qstn #6
Find the charges on the three capacitors connected to a battery as shown in figure (31-E1) Take
C1=2·0 μF, C2=4·0 μF, C3=6·0 μF and V=12 volts.Figure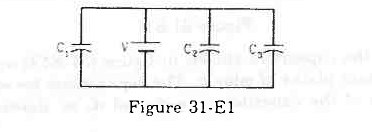
Ans : The capacitances of three capacitors are C₁= 2 μF, C₂= 4 μF and C₃= 6 μF and the voltage of the battery (V) is 12 V.
As the capacitors are connected in parallel, the equivalent capacitance is given by
C_eq = C₁ + C₂ + C₃
= (2 + 4 + 6) μF = 12 μF = 12 × 10^{`` -``6}F

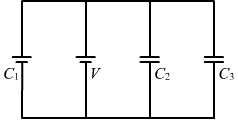
Due to parallel connection, the potential difference across each capacitor is the same and is equal to 12 V.
Therefore, the charge on each capacitor can be calculated as follows:
The charge on the capacitor of capacitance C₁= 2 μF is given by
Q₁= C₁V = (2 × 10^{`` -``6}) × 12 C = 24 × 10^{`` -``6} C = 24 μC
Similarly, the charges on the other two capacitors are given by
Q₂= C₂V = (4 × 10^{`` -``6}) × 12 C = 48 × 10^{`` -``6} C = 48 μC
and
Q₃= C₃V = (6 × 10^{`` -``6}) × 12 C = 72 × 10^{`` -``6} C = 72 μC
Page No 165:

Qstn #7
Three capacitors having capacitances 20 µF, 30 µF and 40 µF are connected in series with a 12 V battery. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
Ans : When the capacitors are connected in series, the equivalent capacitance is given by
`` \frac{1}{{c}_{eq}}=\frac{1}{{c}_{1}}+\frac{1}{{c}_{2}}+\frac{1}{{c}_{3}}``
`` \frac{1}{{c}_{eq}}=\left(\frac{1}{20}+\frac{1}{30}+\frac{1}{40}\right)\times \frac{1}{{10}^{-6}}``
`` \Rightarrow {c}_{eq}=9.23\,\mathrm{\,\mu F\,}``
Because the capacitors are connected in series, the same charge will go to each of them and it is equal to the total charge given by the battery.
Now,
Let the charge at each capacitor be q.
`` \therefore q=CV=(9.23\times {10}^{-6})\times 12``
`` q=110.76\,\mathrm{\,\mu C\,}``
The work done by the battery (W) is given by
`` W\mathit{=}qV``
`` \Rightarrow W=12\times 110.76\times {10}^{-6}``
`` \Rightarrow W=1.33\times {10}^{-3}\,\mathrm{\,J\,}``
Page No 165:

Qstn #8
Find the charge appearing on each of the three capacitors shown in figure (31-E2).
Figure
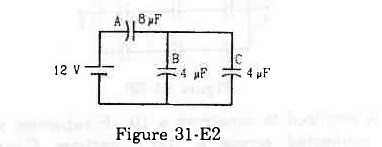
Ans :
Let us first find the equivalent capacitance. It can be observed from the circuit diagram that capacitors B and C are in parallel and are in series with capacitor A.
The equivalent capacitance can be calculated as follows:
`` \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{1}{{C}_{\,\mathrm{\,A\,}}}+\frac{1}{{C}_{\,\mathrm{\,B\,}}+{C}_{\,\mathrm{\,C\,}}}``
`` \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{1}{8}+\frac{1}{4+4}=\frac{1}{8}+\frac{1}{8}``
`` \Rightarrow \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{2}{8}``
`` \Rightarrow {C}_{\,\mathrm{\,eq\,}}=4\,\mathrm{\,\mu \,}F``
Capacitors B and C are parallel and are in series with capacitor A. The equivalent capacitance of capacitors B and C is given by
(4 + 4) μF = 8 μF
It is the same as the capacitance of capacitor A. Therefore, equal potential difference will be there on capacitor A and the system of capacitors B and C.
Now,
Potential difference across capacitor A = 6 V
Thus,
Charge on capacitor A = (8 µF) × (6 V) = 48 µC
And,
Potential difference across capacitors B and C = 6 V
Thus,
Charge on capacitor B = (4 µF) × (6 V) = 24 µF
Charge on capacitor C = (4 µF) × (6 V) = 24 µF
Page No 165:

Qstn #9
Take
C1=4·0 μF and C2=6·0 μFin figure (31-E3). Calculate the equivalent capacitance of the combination between the points indicated.
Figure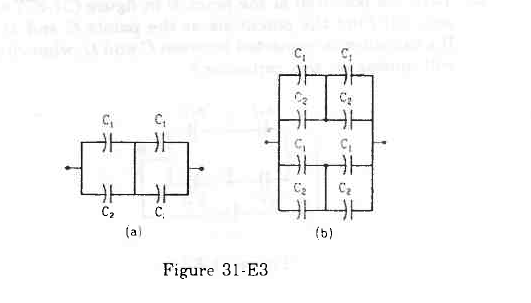
Ans : (a)

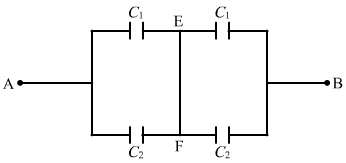
For the combination of capacitors given in figure
(a), the pairs of capacitors C₁and C₂are in parallel.
The equivalent capacitance of each parallel combination of capacitors is given by
C₁+ C₂ = 4 + 6 = 10 μF
The equivalent circuit can be drawn as:

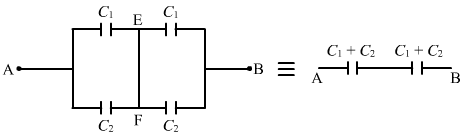
The equivalent capacitance for the above series circuit is given by
`` \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{1}{{C}_{1}+{C}_{2}}+\frac{1}{{C}_{1}+{C}_{2}}=\frac{1}{10}+\frac{1}{10}=\frac{2}{10}``
`` \Rightarrow {C}_{\,\mathrm{\,eq\,}}=5\,\mathrm{\,\mu F\,}``
(b)

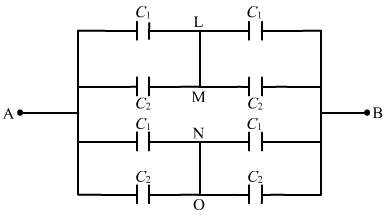
For the combination of capacitors given in figure
(b), the pairs of capacitors C₁and C₂are in parallel.
The equivalent capacitance of each parallel combination of capacitors is given by
C₁+ C₂ = 4 + 6 = 10 μF
The equivalent circuit can be drawn as:

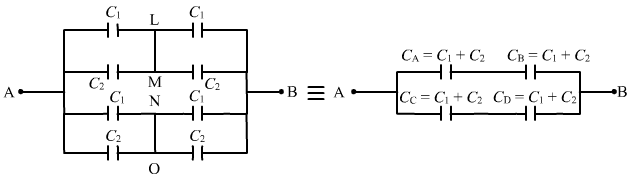
In the above circuit, it can be seen that C_Aand C_B are in series and are in parallel to the series combination of C_Cand C_B.
The equivalent capacitance for the series combination of C_Aand C_Bis given by
`` \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{1}{{C}_{\,\mathrm{\,A\,}}}+\frac{1}{{C}_{\,\mathrm{\,B\,}}}=\frac{1}{{C}_{1}+{C}_{2}}+\frac{1}{{C}_{1}+{C}_{2}}=\frac{1}{10}+\frac{1}{10}=\frac{1}{5}``
`` \Rightarrow {C}_{\,\mathrm{\,eq\,}}=5\,\mathrm{\,\mu F\,}``
Similarly, the equivalent capacitance of the series combination of C_Cand C_Dis 5 μF.
∴ Net equivalent capacitance = 5 + 5 = 10 μF
Page No 166:

Qstn #10
Find the charge supplied by the battery in the arrangement shown in figure (31-E4).
Figure
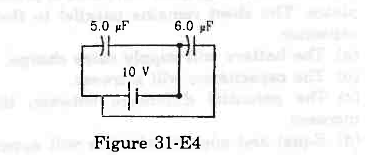
Ans : The equivalent circuit for the given case can be drawn as:

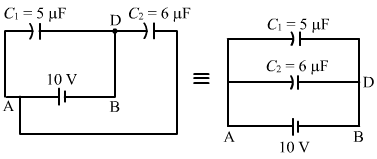
It can be observed that capacitors C₁and C₂ are in parallel.
Therefore, the equivalent capacitance is given by
C_eq = C₁+ C₂
= 5 + 6 = 11 μF
Now,
Charge supplied by the battery = (C_eq)(V) = (11 μF) × (10 V) = 110 μC
Page No 166:

Qstn #11
The outer cylinders of two cylindrical capacitors of capacitance 2⋅2 µF each, are kept in contact and the inner cylinders are connected through a wire. A battery of emf 10 V is connected as shown in figure (31-E5). Find the total charge supplied by the battery to the inner cylinders.
Figure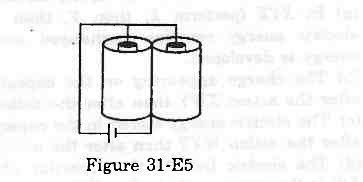
Ans : It is given that the outer cylinders are kept in contact and the inner cylinders are connected through a wire. Thus, the equivalent circuit can be drawn as:

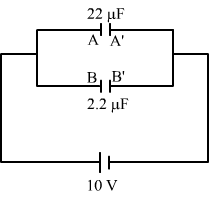
The left plate of the capacitors (A and B) shown in the figure represents the inner plates of the cylindrical capacitors.
As the capacitors are connected in parallel, the potential difference across them is the same.
∴ Magnitude of the charge on each capacitor = CV = (2.2 μF) × (10V) = 22 µC
As plates A and B are connected to the positive terminal of the battery, the charge on each of them is +22 µC.
∴ Net charge on the inner plates = 22 µC + 22 µC = +44 µC
Page No 166:

Qstn #12
Two conducting spheres of radii R₁ and R₂ are kept widely separated from each other. What are their individual capacitances? If the spheres are connected by a metal wire, what will be the capacitance of the combination? Think in terms of series-parallel connections.
Ans : We need to calculate the capacitance of an isolated charged sphere.
Let us assume that the charge on the sphere is Q and its radius is R.
Capacitance of the charged sphere can be found by imagining a concentric sphere of infinite radius consisting of -Q charge.
Potential difference between the spheres = `` \frac{1}{4\pi {\in }_{0}}\frac{Q}{R}`` - 0 = `` \frac{1}{4\pi {\in }_{0}}\frac{Q}{R}``
Capacitance is the ratio of the magnitude of the charge on each conductor to the potential difference between them.
`` C=\frac{Q}{{\displaystyle \frac{1}{4\pi {\in }_{0}}\frac{Q}{R}}}=4\pi {\in }_{0}R``
Therefore, the capacitances of spheres of radii R₁ and R₂ are C₁ and C₂, respectively. They are given by
`` {C}_{1}=4\pi {\in }_{0}{R}_{1}``
`` {C}_{2}=4\,\mathrm{\,\pi \,}{\in }_{0}{R}_{2}``
If the spheres are connected by a metal wire, the charge will flow from one sphere to another till their potentials become the same.
As there potentials become the same, the potential difference between the conductors for both the capacitors also becomes the same. Thus, it can be concluded that the capacitors are connected in parallel.
Thus, the capacitance of the combination is given by
`` {C}_{\,\mathrm{\,eq\,}}`` = C₁ + C₂
`` =4\,\mathrm{\,\pi \,}{\in }_{0}\left({R}_{1}+{R}_{2}\right)``
Page No 166: