NEET-XII-Physics
31: Capacitors
- #9Take
C1=4·0 μF and C2=6·0 μFin figure (31-E3). Calculate the equivalent capacitance of the combination between the points indicated.
Figure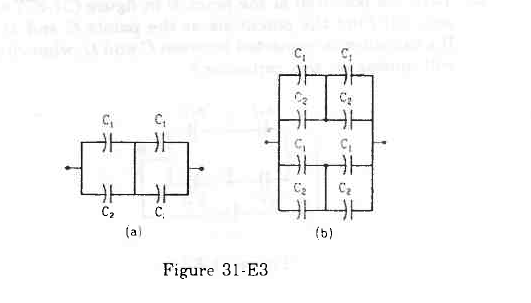
Ans : (a)
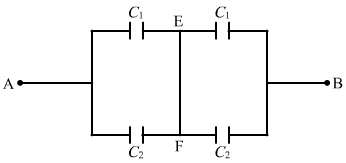
For the combination of capacitors given in figure
(a), the pairs of capacitors C1 and C2 are in parallel.
The equivalent capacitance of each parallel combination of capacitors is given by
C1 + C2 = 4 + 6 = 10 μF
The equivalent circuit can be drawn as:
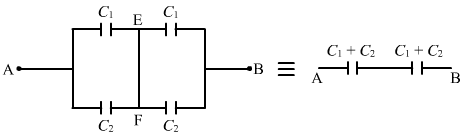
The equivalent capacitance for the above series circuit is given by
`` \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{1}{{C}_{1}+{C}_{2}}+\frac{1}{{C}_{1}+{C}_{2}}=\frac{1}{10}+\frac{1}{10}=\frac{2}{10}``
`` \Rightarrow {C}_{\,\mathrm{\,eq\,}}=5\,\mathrm{\,\mu F\,}``
(b)
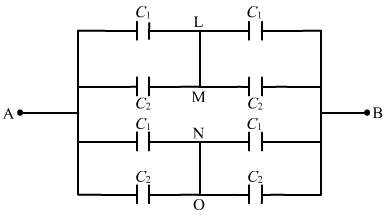
For the combination of capacitors given in figure
(b), the pairs of capacitors C1 and C2 are in parallel.
The equivalent capacitance of each parallel combination of capacitors is given by
C1 + C2 = 4 + 6 = 10 μF
The equivalent circuit can be drawn as:
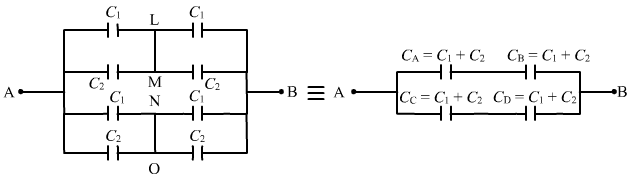
In the above circuit, it can be seen that CA and CB are in series and are in parallel to the series combination of CC and CB.
The equivalent capacitance for the series combination of CA and CB is given by
`` \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{1}{{C}_{\,\mathrm{\,A\,}}}+\frac{1}{{C}_{\,\mathrm{\,B\,}}}=\frac{1}{{C}_{1}+{C}_{2}}+\frac{1}{{C}_{1}+{C}_{2}}=\frac{1}{10}+\frac{1}{10}=\frac{1}{5}``
`` \Rightarrow {C}_{\,\mathrm{\,eq\,}}=5\,\mathrm{\,\mu F\,}``
Similarly, the equivalent capacitance of the series combination of CC and CD is 5 μF.
∴ Net equivalent capacitance = 5 + 5 = 10 μF
Page No 166: