NEET-XII-Physics
31: Capacitors
- #8Find the charge appearing on each of the three capacitors shown in figure (31-E2).
Figure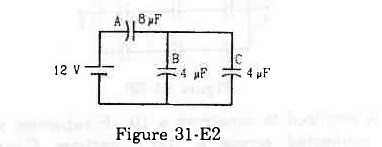 Ans :
Ans :
Let us first find the equivalent capacitance. It can be observed from the circuit diagram that capacitors B and C are in parallel and are in series with capacitor A.
The equivalent capacitance can be calculated as follows:
`` \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{1}{{C}_{\,\mathrm{\,A\,}}}+\frac{1}{{C}_{\,\mathrm{\,B\,}}+{C}_{\,\mathrm{\,C\,}}}``
`` \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{1}{8}+\frac{1}{4+4}=\frac{1}{8}+\frac{1}{8}``
`` \Rightarrow \frac{1}{{C}_{\,\mathrm{\,eq\,}}}=\frac{2}{8}``
`` \Rightarrow {C}_{\,\mathrm{\,eq\,}}=4\,\mathrm{\,\mu \,}F``
Capacitors B and C are parallel and are in series with capacitor A. The equivalent capacitance of capacitors B and C is given by
(4 + 4) μF = 8 μF
It is the same as the capacitance of capacitor A. Therefore, equal potential difference will be there on capacitor A and the system of capacitors B and C.
Now,
Potential difference across capacitor A = 6 V
Thus,
Charge on capacitor A = (8 µF) × (6 V) = 48 µC
And,
Potential difference across capacitors B and C = 6 V
Thus,
Charge on capacitor B = (4 µF) × (6 V) = 24 µF
Charge on capacitor C = (4 µF) × (6 V) = 24 µF
Page No 165: