29: Electric Field And Potential : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

29: Electric Field and Potential

with Solutions - page 3

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #4
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = -1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm^-1
(b) may be equal to 20 Vcm^-1
(c) may be greater than 20 Vcm^-1
(d) may be less than 20 Vcm^-1
digAnsr: b,c
Ans : (b) may be equal to 20 Vcm^-1
(c) may be greater than 20 Vcm^-1
Change in the electric potential, dV = 40 V
Change in length, `` ∆r`` = -1-1 = -2 cm
Electric field,
`` E=\frac{-dV}{dr}``
`` \Rightarrow E=-\frac{40\,\mathrm{\,V\,}}{-2}``
`` \Rightarrow E=20{\,\mathrm{\,Vcm\,}}^{-1}``
This is the value of the electric field along the x axis.
Electric field is maximum along the direction in which the potential decreases at the maximum rate. But here, direction in which the potential decreases at the maximum rate may or may not be along the x-axis. From the given information,the direction of maximum decrease in potential cannot be found out accurately. So, E can be greater than 20 V/cm in the direction of maximum decrease in potential.
So, the electric field at the origin may be equal to or greater than 20 Vcm^-1.
Page No 120:

Qstn #5
Which of the following quantities does not depend on the choice of zero potential or zero potential energy?
(a) Potential at a point
(b) Potential difference between two points
(c) Potential energy of a two-charge system
(d) Change in potential energy of a two-charge system
digAnsr: b,d
Ans : (b) Potential difference between two points
(d) Change in potential energy of a two-charge system
Potential and potential energy depend on the choice of a reference point of zero potential or zero potential energy. But the difference of potential and energy does not depend on the choice of the reference point. Hence, the correct options are
(b) and
(d).
Page No 120:

Qstn #6
An electric dipole is placed in an electric field generated by a point charge.
(a) The net electric force on the dipole must be zero.
(b) The net electric force on the dipole may be zero.
(c) The torque on the dipole due to the field must be zero.
(d) The torque on the dipole due to the field may be zero.
digAnsr: d
Ans : (d) The torque on the dipole due to the field may be zero.
Torque acting on a dipole placed in an electric field,
`` \tau =r\times F``
`` =rF\,\mathrm{\,sin\,}\theta ,``
where `` \theta `` is the angle between the force F and the arm of the couple.
So, for `` \theta ``=0 or pi ,the torque will be zero. Hence, the amount of torque acting on the dipole depends on the orientation of the dipole in the given electric field.
Page No 120:

Qstn #7
A proton and an electron are placed in a uniform electric field.
(a) The electric forces acting on them will be equal.
(b) The magnitudes of the forces will be equal.
(c) Their accelerations will be equal.
(d) The magnitudes of their accelerations will be equal.
digAnsr: b
Ans : (b) The magnitudes of the forces will be equal.
We know:
`` \stackrel{\to }{F}=q\stackrel{\to }{E}``
For an electron and a proton, the value of q will be same, but the sign will be opposite.
Hence, they will experience a force that will be equal in magnitude but opposite in direction.
Now,
`` \stackrel{\to }{F}=q\stackrel{\to }{E}=m\stackrel{\to }{a}``
`` \Rightarrow \stackrel{\to }{a}=\frac{q\stackrel{\to }{E}}{m}``
As the electron and proton have different values of mass m, they will have different magnitudes of acceleration. Also, they will differ in direction due to the opposite signs of q.
Page No 120:

Qstn #8
The electric field in a region is directed outward and is proportional to the distance r from the origin. Taking the electric potential at the origin to be zero,
(a) it is uniform in the region
(b) it is proportional to r
(c) it is proportional to r²
(d) it increases as one moves away from the origin
digAnsr: c
Ans : (c) it is proportional to r²
Given:
E`` \propto ``r and V = 0 at r =0
`` \Rightarrow ``E = kr
Also, E = `` \frac{-dV}{dr}``
`` \therefore V=-\int Edr``
`` \Rightarrow V=-\int krdr``
`` \Rightarrow V=-k\frac{{r}^{2}}{2}+C``
Using the condition, V = 0 at r = 0, we get C =0.
Therefore,
`` V=-k\frac{{r}^{2}}{2}``
`` \Rightarrow V\propto {r}^{2}``
Page No 121:

#
Section : iv

Qstn #1
Find the dimensional formula of ε₀.
Ans : By Coulomb's Law,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` \Rightarrow {\epsilon }_{0}=\frac{1}{4\,\mathrm{\,\pi \,}F}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
Using [F] = [MLT^-2]
[r] = [M⁰L¹T⁰]
[q] = [M⁰L⁰T¹A¹], we get
[ε₀] = [M^-1L^-3T⁴A²]
Page No 121:

Qstn #2
A charge of 1.0 C is placed at the top of your college building and another equal charge at the top of your house. Take the separation between the two charges to be 2.0 km. Find the force exerted by the charges on each other. How many times your weight is this force?
Ans : Given:
q₁ = q₂ = q = 1.0 C
Distance between the charges, r = 2 km = 2 × 10³ m
By Coulomb's Law, electrostatic force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` F=9\times {10}^{9}\times \frac{1\times 1}{{\left(2\times {10}^{3}\right)}^{2}}``
`` =2.25\times {10}^{3}\,\mathrm{\,N\,}``
Let my mass, m, be 50 kg.
Weight of my body, W = mg
⇒ W = 50 × 10 N = 500 N
Now,
`` \frac{\text{W}\,\mathrm{\,eight\,}\,\mathrm{\,of\,}\text{my}\,\mathrm{\,body\,}}{\text{F}\,\mathrm{\,orce\,}\,\mathrm{\,between\,}\text{the}\,\mathrm{\,charges\,}}=\frac{500}{2.25\times {10}^{3}}=\frac{1}{4.5}``
So, the force between the charges is 4.5 times the weight of my body.
Page No 121:

Qstn #3
At what separation should two equal charges, 1.0 C each, be placed, so that the force between them equals the weight of a 50 kg person?
Ans : Given:
Magnitude of charges, q₁ = q₂ = 1 C
Electrostatic force between them, F = Weight of a 50 kg person = mg = 50 × 9.8 = 490 N
Let the required distance be r.
By Coulomb's Law, electrostatic force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` \Rightarrow 490=\frac{9\times {10}^{9}\times 1\times 1}{{r}^{2}}``
`` \Rightarrow {r}^{2}=\frac{9\times {10}^{9}}{490}``
`` ``
`` \Rightarrow r=\sqrt{\frac{9}{49}\times {10}^{8}}=\frac{3}{7}\times {10}^{4}\,\mathrm{\,m\,}=4.3\times {10}^{3}\,\mathrm{\,m\,}``
`` ``
Page No 121:

Qstn #4
Two equal charges are placed at a separation of 1.0 m. What should be the magnitude of the charges, so that the force between them equals the weight of a 50 kg person?
Ans : Let the magnitude of each charge be q.
Separation between them, r = 1 m
Force between them, F = 50 × 9.8 = 490 N
By Coulomb's Law force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` \Rightarrow 490=9\times {10}^{9}\times \frac{{q}^{2}}{{1}^{2}}``
`` \Rightarrow {q}^{2}=54.4\times {10}^{-9}``
`` \Rightarrow q=\sqrt{54.4\times {10}^{-9}}=23.323\times {10}^{-5}\,\mathrm{\,C\,}``
`` \,\mathrm{\,Or\,}q=2.3\times {10}^{-4}\,\mathrm{\,C\,}``
Page No 121:

Qstn #5
Find the electric force between two protons separated by a distance of 1 fermi (1 fermi = 10^-15 m). The protons in a nucleus remain at a separation of this order.
Ans : We know:
Charge on a proton, q = 1.6 × 10^-19 C
Given, separation between the charges, r = 10^-¹⁵ m
By Coulomb's Law, electrostatic force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` \Rightarrow F=9\times {10}^{9}\times \frac{{\left(1.6\times {10}^{-19}\right)}^{2}}{{\left({10}^{-15}\right)}^{2}}``
`` \Rightarrow F=230\,\mathrm{\,N\,}``
Page No 121:

Qstn #6
Two charges 2.0 × 10^-6 C and 1.0 × 10^-6 C are placed at a separation of 10 cm. Where should a third charge be placed, such that it experiences no net force due to these charges?
Ans : Given:
`` {q}_{1}=2.0\times {10}^{-6}\,\mathrm{\,C\,}``
`` {q}_{2}=1.0\times {10}^{-6}\,\mathrm{\,C\,}``
Let the third charge, q, be placed at a distance of x cm from charge q₁_, as shown in the figure.

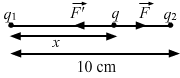
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{Q}_{1}{Q}_{2}}{{r}^{2}}``
Force on charge q due to q₁,
`` F=\frac{9\times {10}^{9}\times 2.0\times {10}^{-6}\times q}{{x}^{2}}``
Force on charge q due to q₂,
`` F\text{'}=\frac{9\times {10}^{9}\times {10}^{-6}\times q}{{\left(10-x\right)}^{2}}``
`` ``
According to the question,
`` F-F\text{'}=0``
`` \Rightarrow F=F\text{'}``
`` \Rightarrow \frac{9\times {10}^{9}\times 2\times {10}^{-6}\times q}{{x}^{2}}=\frac{9\times {10}^{9}\times {10}^{-6}\times q}{{\left(10-x\right)}^{2}}``
`` \Rightarrow {x}^{2}=2{\left(10-x\right)}^{2}``
`` \Rightarrow {x}^{2}-40x+200=0``
`` \Rightarrow x=20\pm 10\sqrt{2}``
`` \Rightarrow x=5.9\,\mathrm{\,cm\,}(\because x\ne 20+10\sqrt{2})``
So, the third charge should be placed at a distance of 5.9 cm from q₁.
Page No 121:

Qstn #7
Suppose the second charge in the previous problem is -1.0 × 10^-⁶ C. Locate the position where a third charge will not experience a net force.
Ans : Given:
`` {q}_{1}=2\times {10}^{-6}\,\mathrm{\,C\,}``
`` {q}_{2}=-1\times {10}^{-6}\,\mathrm{\,C\,}``
Since both the charges are opposite in nature, the third charge cannot be placed between them. Let the third charge, q, be placed at a distance of x cm from charge q₁, as shown in the figure.

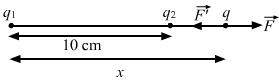
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{Q}_{1}{Q}_{2}}{{r}^{2}}``
So, force on charge q due to q₁,
`` F=\frac{9\times {10}^{9}\times 2.0\times {10}^{-6}\times q}{{x}^{2}}``
Force on charge q due to q₂,
`` F\text{'}=\frac{9\times {10}^{9}\times {10}^{-6}\times q}{{\left(10-x\right)}^{2}}``
`` \,\mathrm{\,According\,}\,\mathrm{\,to\,}\text{the}\,\mathrm{\,question\,},``
`` F-F\text{'}=0``
`` \Rightarrow F=F\text{'}``
`` \Rightarrow \frac{9\times {10}^{9}\times 2\times {10}^{-6}\times q}{{x}^{2}}=\frac{9\times {10}^{9}\times {10}^{-6}\times q}{{\left(x-10\right)}^{2}}``
`` \Rightarrow {x}^{2}=2{\left(x-10\right)}^{2}``
`` \Rightarrow {x}^{2}-40x+200=0``
`` \Rightarrow x=20\pm 10\sqrt{2}\,\mathrm{\,m\,}``
`` \Rightarrow x=34.14\,\mathrm{\,cm\,}(\because x\ne 20-10\sqrt{2})``
Page No 121:

Qstn #8
Two charged particles are placed 1.0 cm apart. What is the minimum possible magnitude of the electric force acting on each charge?
Ans : We know that minimum charge on a body (q) = charge on an electron
⇒ q = 1.6 × 10^-19 C
Given:
Separation between the charges, r = 1 cm = 10^-2 m
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` \Rightarrow F=\frac{9\times {10}^{9}\times {\left(1.6\times {10}^{-19}\right)}^{2}}{{\left({10}^{-2}\right)}^{2}}``
`` \Rightarrow F=2.3\times {10}^{-24}\,\mathrm{\,N\,}``
Page No 121:

Qstn #9
Estimate the number of electrons in 100 g of water. How much is the total negative charge on these electrons?
Ans : Molecular mass of water= 18 g
Number of molecules in 18 g of H₂O = Avogadro's number
= 6.023 × 10²³
Number of electrons in 1 molecule of H₂O = (2 × 1) + 8 = 10
Number of electrons in 6.023 × 10²³ molecules of H₂O = 6.023 × 10²⁴
That is, number of electrons in 18 g of H₂O = 6.023 × 10²⁴
So, number of electrons in 100 g of H₂O = `` \frac{6.023\times {10}^{24}}{18}\times 100``
= 3.34 × 10²⁵
∴ Total charge = 3.34 × 10²⁵ × 1.6 × 10^-19
= 5.34 × 10⁶ C
Page No 121: