29: Electric Field And Potential : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

29: Electric Field and Potential

with Solutions - page 4

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #10
Suppose all the electrons of 100 g water are lumped together to form a negatively-charged particle and all the nuclei are lumped together to form a positively-charged particle. If these two particles are placed 10.0 cm away from each other, find the force of attraction between them. Compare it with your weight.
Ans : Molecular mass of water= 18 g
So, number of atoms in 18 g of H₂O = Avogadro's number
= 6.023 × 10²³
Number of electrons in 1 atom of H₂O = (2 × 1) + 8 = 10
Number of electrons in 6.023 × 10²³ atoms of H₂O= 6.023 × 10²⁴
That is, number of electrons in 18 g of H₂O = 6.023 × 10²⁴
So, number of electrons in 100 g of H₂O = `` \frac{6.023\times {10}^{24}}{18}\times 100``
= 3.34 × 10²⁵
Total charge = 3.34 × 10²⁵ × (-1.6 × 10^-19)
=- 5.34 × 10⁶ C
So total charge of electrons in 100 gm of water, q₁ = -5.34 × 10⁶ C
Similarly, total charge of protons in 100 gm of water, q₂= +5.34 × 10⁶ C
Given, r = 10 cm = 0.1 m
By Coulomb's Law, electrostatic force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` =9\times {10}^{9}\times \frac{5.34\times {10}^{6}\times 5.34\times {10}^{6}}{{10}^{-2}}``
`` =2.56\times {10}^{25}\,\mathrm{\,N\,}``
This force will be attractive in nature.
Result shows that the electrostatic force is much stronger than the gravitational force between any us and earth(weight=gravitational force between us and earth).
Page No 121:

Qstn #11
Consider a gold nucleus to be a sphere of radius 6.9 fermi in which protons and neutrons are distributed. Find the force of repulsion between two protons situated at largest separation. Why do these protons not fly apart under this repulsion?
Ans : Given, radius of the sphere, R = 6.9 fermi
So, the largest separation between two protons = 2R = 13.8 fermi
Charge on a proton, q = `` 1.6\times {10}^{-19}\,\mathrm{\,C\,}``
By Coulomb's Law, force of repulsion,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` \Rightarrow F=9\times {10}^{9}\times \frac{{\left(1.6\times {10}^{-19}\right)}^{2}}{{\left(2R\right)}^{2}}=1.2\,\mathrm{\,N\,}``
Inside the nucleus, another short-range attractive force (nuclear force) acts on the protons. That's why these protons do not fly apart due to the Coulombian repulsion.
Page No 121:

Qstn #12
Two insulating small spheres are rubbed against each other and placed 1 cm apart. If they attract each other with a force of 0.1 N, how many electrons were transferred from one sphere to the other during rubbing?
Ans : Given:
Force of attraction between the spheres, F = 0.1 N
Separation between the spheres, r = 10^-2 m
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
Let the no. of electrons transferred from one sphere to the other be n. Then,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{\left(nq\right)}^{2}}{{r}^{2}}``
`` \Rightarrow 0.1=\frac{9\times {10}^{-9}\times {n}^{2}\times {\left(1.6\times {10}^{-19}\right)}^{2}}{{10}^{-4}}``
`` \Rightarrow {n}^{2}=\frac{0.1\times {10}^{-4}}{9\times {10}^{9}\times 1.6\times 1.6\times {10}^{-38}}``
`` \Rightarrow n=2\times {10}^{11}``
Page No 121:

Qstn #13
An NaCl molecule is bound due to the electric force between the sodium and the chlorine ions when one electron of sodium is transferred to chlorine. Taking the separation between the ions to be 2.75 × 10^-8 cm, find the force of attraction between them. State the assumptions (if any) that you have made.
Ans : Let the given separation between the ions, i.e. 2.75 × 10^-8 cm, be the separation between the transferred electron and the sodium nucleus.
Net charge on thechlorine ion, q₁ = `` -1.6\times {10}^{-19}`` C
Net charge on the sodium ion, q₂ = `` 1.6\times {10}^{-19}`` C
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` =\frac{9\times {10}^{9}\times {\left(1.6\times {10}^{-19}\right)}^{2}}{{\left(2.75\times {10}^{-10}\right)}^{2}}``
`` =3.05\times {10}^{-9}\,\mathrm{\,N\,}``
Page No 121:

Qstn #14
Find the ratio of the electrical and gravitational forces between two protons.
Ans : We know that the mass of a proton, m = 1.67 × 10^-27 kg
Charge on a proton, q = 1.6 × 10^-19 C
Gravitational constant, `` \,\mathrm{\,G\,}=6.67\times {10}^{-11}\,\mathrm{\,N\,}-{\,\mathrm{\,m\,}}^{2}/{\,\mathrm{\,kg\,}}^{2}``
Electrostatic force,
`` {F}_{e}=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}^{2}}{{r}^{2}}``
`` ``
Gravitational force,
`` {F}_{g}=G\frac{{m}^{2}}{{r}^{2}}``
`` \Rightarrow \frac{{F}_{e}}{{F}_{g}}=\frac{{q}^{2}}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}G{m}^{2}}``
`` =\frac{9\times {10}^{9}\times {\left(1.6\times {10}^{-19}\right)}^{2}}{6.67\times {10}^{-11}\times {\left(1.67\times {10}^{-27}\right)}^{2}}``
`` =1.23\times {10}^{36}``
Page No 121:

Qstn #15
Suppose an attractive nuclear force acts between two protons which may be written as F=Ce^-kr/r².

#15-a
Write down the dimensional formulae and appropriate SI units of C and k.
Ans : Given, nuclear force of attraction, `` F=C\frac{{e}^{-Kr}}{{r}^{2}}``
Here e^-Kr is just a pure number, i.e. a dimensionless quantity. So,
`` \left[C\right]=\left[F\right]\times \left[{r}^{2}\right]``
`` \left[C\right]=\left[{\,\mathrm{\,MLT\,}}^{-2}\right]\times \left[{\,\mathrm{\,L\,}}^{2}\right]``
`` \left[\,\mathrm{\,C\,}\right]=\left[{\,\mathrm{\,ML\,}}^{3}{\,\mathrm{\,T\,}}^{-2}\right]``
`` \,\mathrm{\,And\,}\left[K\right]=\frac{1}{\left[r\right]}=\left[{\,\mathrm{\,L\,}}^{-1}\right]``

#15-b
Suppose that k = 1 fermi^-1 and that the repulsive electric force between the protons is just balanced by the attractive nuclear force when the separation is 5 fermi. Find the value of C.
Ans : By Coulomb's Law, electric force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{e}^{2}}{{r}^{2}}``
Taking `` r=5\times {10}^{-15}\,\mathrm{\,m\,}``, we get
`` F=\frac{9\times {10}^{9}\times {\left(1.6\times {10}^{-19}\right)}^{2}}{{\left(5\times {10}^{-15}\right)}^{2}}``
And nuclear force, F = Ce^-kr/r²
Taking r = 5 × 10^-15m and k = 1 fermi^-1, we get
`` F=\frac{C\times {10}^{-5}}{{\left(5\times {10}^{-15}\right)}^{2}}``
`` ``
Comparing both the forces, we get
`` C=3.4\times {10}^{-26}\,\mathrm{\,N\,}-{\,\mathrm{\,m\,}}^{2}``
Page No 121:

Qstn #16
Three equal charges, 2.0 × 10^-⁶ C each, are held at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the other two.
Ans : Since all the charges are of equal magnitude, the force on the charge at A due to the charges at B and C will be of equal magnitude. (As shown in the figure)
That is, `` {F}_{\,\mathrm{\,BA\,}}={F}_{\,\mathrm{\,CA\,}}=F\left(\,\mathrm{\,say\,}\right)``

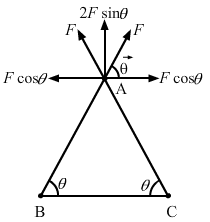
The horizontal components of force cancel each other and the net force on the charge at A,
`` F\text{'}={F}_{\,\mathrm{\,BA\,}}\,\mathrm{\,sin\,}\theta +{F}_{\,\mathrm{\,CA\,}}\,\mathrm{\,sin\,}\theta ``
`` \,\mathrm{\,F\,}\text{'}=2F\,\mathrm{\,sin\,}\theta ``
`` ``
Given: r = 5 cm =0.05 m
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` F\text{'}=\frac{2\times 9\times {10}^{9}\times {\left(2\times {10}^{-6}\right)}^{2}\times {\displaystyle \,\mathrm{\,sin\,}60°}}{{\left(0.05\right)}^{2}}``
`` F\text{'}=\frac{2\times 9\times {10}^{9}\times {\left(2\times {10}^{-6}\right)}^{2}\times {\displaystyle \frac{\sqrt{3}}{2}}}{{\left(0.05\right)}^{2}}``
F' = 24.9 N
Page No 121:

Qstn #17
Four equal charges of 2.0 × 10^-6 C each are fixed at the four corners of a square of side 5 cm. Find the Coulomb’s force experienced by one of the charges due to the other three.
Ans : Given,
Magnitude of the charges, `` q=2\times {10}^{-6}\,\mathrm{\,C\,}``
Side of the square, `` a=5\,\mathrm{\,cm\,}=0.05\,\mathrm{\,m\,}``
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``

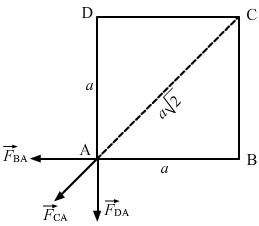
So, force on the charge at A due to the charge at B,
`` {\stackrel{\to }{F}}_{\,\mathrm{\,BA\,}}=\frac{9\times {10}^{9}\times {\left(2\times {10}^{-6}\right)}^{2}}{{\left(0.05\right)}^{2}}``
`` =\frac{9\times {10}^{9}\times 4\times {10}^{-12}}{25\times {10}^{-4}}``
`` =14.4\,\mathrm{\,N\,}``
`` ``
Force on the charge at A due to the charge at C,
`` {\stackrel{\to }{F}}_{\,\mathrm{\,CA\,}}=\frac{9\times {10}^{9}\times {\left(2\times {10}^{-6}\right)}^{2}}{{\left(\sqrt{2}\times 0.05\right)}^{2}}``
`` =\frac{9\times {10}^{9}\times 4\times {10}^{-12}}{25\times 2\times {10}^{-4}}``
`` =7.2\,\mathrm{\,N\,}``
Force on the charge at A due to the charge at D,
`` {\stackrel{\to }{F}}_{\,\mathrm{\,DA\,}}={\stackrel{\to }{F}}_{\,\mathrm{\,BA\,}}``
The resultant force at A, F'= `` {\stackrel{\to }{F}}_{\,\mathrm{\,BA\,}}+{\stackrel{\mathit{\to }}{\mathit{F}}}_{\,\mathrm{\,CA\,}}+{\stackrel{\mathit{\to }}{\mathit{F}}}_{\,\mathrm{\,DA\,}}``
The resultant force of `` {\stackrel{\to }{F}}_{\,\mathrm{\,DA\,}}\,\mathrm{\,and\,}{\stackrel{\to }{F}}_{\,\mathrm{\,BA\,}}`` will be `` \sqrt{2}{F}_{\,\mathrm{\,BA\,}}`` in the direction of `` {\stackrel{\mathit{\to }}{F}}_{\,\mathrm{\,CA\,}}``. Hence, the resultant force,
`` F\text{'}=14.4\sqrt{2}+7.2``
`` =27.56\,\mathrm{\,N\,}``
Page No 121:

Qstn #18
A hydrogen atom contains one proton and one electron. It may be assumed that the electron revolves in a circle of radius 0.53 angstrom (1 angstrom = 10^-10 m and is abbreviated as Å) with the proton at the centre. The hydrogen atom is said to be in the ground state in this case. Find the magnitude of the electric force between the proton and the electron of a hydrogen atom in its ground state.
Ans : Given:
Separation between the two charges, r = 0.53 Å = 0.53 × 10^-10 m
`` {q}_{1}={q}_{2}=e``
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
`` F=\frac{9\times {10}^{9}\times {\left(1.6\times {10}^{-19}\right)}^{2}}{{\left(0.53\times {10}^{-10}\right)}^{2}}``
`` =8.2\times {10}^{-8}\,\mathrm{\,N\,}``
Page No 121:

Qstn #19
Find the speed of the electron in the ground state of a hydrogen atom. The description of ground state is given in the previous problem.
Ans : Given:
Separation between the two charges, r = 0.53 Å = 0.53 × 10^-10 m
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}{q}_{2}}{{r}^{2}}``
Here, `` {q}_{1}={q}_{2}=e``
`` \Rightarrow F=\frac{9\times {10}^{9}\times {\left(1.6\times {10}^{-19}\right)}^{2}}{{\left(0.53\times {10}^{-10}\right)}^{2}}``
`` =8.2\times {10}^{-8}\,\mathrm{\,N\,}``
Now, mass of an electron, M_e = 9.12 × 10^-³¹ kg
The necessary centripetal force is provided by the Coulombian force.
`` \Rightarrow {F}_{e}=\frac{{M}_{e}{v}^{2}}{r}``
`` \Rightarrow {v}^{2}=0.4775\times {10}^{13}``
`` =4.775\times {10}^{12}``
`` \Rightarrow v=2.18\times {10}^{6}\,\mathrm{\,m\,}/\,\mathrm{\,s\,}``
Page No 121:

Qstn #20
Ten positively-charged particles are kept fixed on the x-axis at points x = 10 cm, 20 cm, 30 cm, ...., 100 cm. the first particle has a charge 1.0 × 10^-8 C, the second 8 × 10^-8 C, the third 27 × 10^-8 C and so on. The tenth particle has a charge 1000 × 10^-8 C. Find the magnitude of the electric force acting on a 1 C charge placed at the origin.
Ans : By Coulomb's Law, force (F) on charge q due to one charge,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}_{1}q}{{r}^{2}}``
So, net force due to ten charges,
`` F={F}_{1}+{F}_{2}+{F}_{3}+.....+{F}_{10}``
`` =9\times {10}^{9}\times \left[\frac{1.0}{{\left(0.10\right)}^{2}}+\frac{8}{{\left(.20\right)}^{2}}+\frac{27}{{\left(.30\right)}^{2}}+......\frac{1000}{{\left(1.0\right)}^{2}}\right]{10}^{-8}``
`` =\frac{9\times {10}^{9}\times {10}^{-8}}{{10}^{-2}}\left[1+2+3+......10\right]``
`` =9\times {10}^{3}\times 55``
`` =4.95\times {10}^{5}\,\mathrm{\,N\,}``
Page No 121:

Qstn #21
Two charged particles with charge 2.0 × 10^-8 C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
Ans : Given:
Magnitude of the charges, q = 2.0 × 10^-8 C
Separation between the charges, r = 1 m
The tension in the string will be same as the electrostatic force between the charged particles.
So, `` T=F``
By Coulomb's Law,

`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{q}^{2}}{{r}^{2}}``
`` \Rightarrow T=\frac{9\times {10}^{9}\times {\left(2.0\times {10}^{-8}\right)}^{2}}{{1}^{2}}``
`` =3.6\times {10}^{-6}\,\mathrm{\,N\,}``
Page No 121:

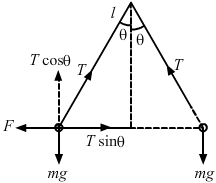
Qstn #22
Two identical balls, each with a charge of 2.00 × 10^-7 C and a mass of 100 g, are suspended from a common point by two insulating strings, each 50 cm long. The balls are held 5.0 cm apart and then released. Find
Ans : Given:
Magnitude of the charges, q = 2.0 × 10^-7 C
Separation between the charges, `` r=5\times {10}^{-2}\,\mathrm{\,m\,}``
Length of the string, `` l=50\,\mathrm{\,cm\,}=50\times {10}^{-2}\,\mathrm{\,m\,}``
Mass of the balls, m = 100 g = 0.1 kg