NEET-XII-Physics
29: Electric Field and Potential
- #7Suppose the second charge in the previous problem is -1.0 × 10-6 C. Locate the position where a third charge will not experience a net force.Ans : Given:
`` {q}_{1}=2\times {10}^{-6}\,\mathrm{\,C\,}``
`` {q}_{2}=-1\times {10}^{-6}\,\mathrm{\,C\,}``
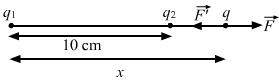
Since both the charges are opposite in nature, the third charge cannot be placed between them. Let the third charge, q, be placed at a distance of x cm from charge q1, as shown in the figure.
By Coulomb's Law, force,
`` F=\frac{1}{4\,\mathrm{\,\pi \,}{\epsilon }_{0}}\frac{{Q}_{1}{Q}_{2}}{{r}^{2}}``
So, force on charge q due to q1,
`` F=\frac{9\times {10}^{9}\times 2.0\times {10}^{-6}\times q}{{x}^{2}}``
Force on charge q due to q2,
`` F\text{'}=\frac{9\times {10}^{9}\times {10}^{-6}\times q}{{\left(10-x\right)}^{2}}``
`` \,\mathrm{\,According\,}\,\mathrm{\,to\,}\text{the}\,\mathrm{\,question\,},``
`` F-F\text{'}=0``
`` \Rightarrow F=F\text{'}``
`` \Rightarrow \frac{9\times {10}^{9}\times 2\times {10}^{-6}\times q}{{x}^{2}}=\frac{9\times {10}^{9}\times {10}^{-6}\times q}{{\left(x-10\right)}^{2}}``
`` \Rightarrow {x}^{2}=2{\left(x-10\right)}^{2}``
`` \Rightarrow {x}^{2}-40x+200=0``
`` \Rightarrow x=20\pm 10\sqrt{2}\,\mathrm{\,m\,}``
`` \Rightarrow x=34.14\,\mathrm{\,cm\,}(\because x\ne 20-10\sqrt{2})``
Page No 121: