28: Heat Transfer : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

28: Heat Transfer

with Solutions - page 4

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #14
On a winter day when the atmospheric temperature drops to -10°C, ice forms on the surface of a lake.
Ans : Thermal conductivity, K = 1.7 W/m°C
Density of water, ρ_ω = 10² kg/m³
Latent heat of fusion of ice, L_ice = 3.36 × 10⁵ J/kg
Length, l = 10 × 10^-2 m

#14-a
Calculate the rate of increase of thickness of the ice when 10 cm of the ice is already formed.
Ans : Rate of flow of heat is given by
`` \frac{\,\mathrm{\,\Delta Q\,}}{\,\mathrm{\,\Delta \,}t}=\frac{\left({\,\mathrm{\,T\,}}_{1}-{\,\mathrm{\,T\,}}_{2}\right)·\,\mathrm{\,KA\,}}{l}``
`` \Rightarrow \frac{l}{\,\mathrm{\,\Delta \,}t}=\frac{\left({T}_{1}-{T}_{2}\right)\mathit{·}KA}{\,\mathrm{\,\Delta Q\,}}``
`` =\frac{\,\mathrm{\,K\,}·\,\mathrm{\,A\,}\left({\,\mathrm{\,T\,}}_{1}-{\,\mathrm{\,T\,}}_{2}\right)}{\,\mathrm{\,m\,}·\,\mathrm{\,L\,}}``
`` =\frac{\,\mathrm{\,KA\,}\left({\,\mathrm{\,T\,}}_{1}-{\,\mathrm{\,T\,}}_{2}\right)}{\left(\,\mathrm{\,A\,}l·{\,\mathrm{\,\rho \,}}_{\,\mathrm{\,\omega \,}}\right)\,\mathrm{\,L\,}}``
`` =\frac{\left(1.7\right)\left(0-10\right)}{\left(10\times {10}^{-2}\right)\times {10}^{3}\times 3.36\times {10}^{5}}``
`` =\frac{17}{3.36}\times {10}^{-7}``
`` =5.059\times {10}^{-7}\,\mathrm{\,m\,}/\,\mathrm{\,s\,}``
`` =5\times {10}^{-7}\,\mathrm{\,m\,}/\,\mathrm{\,s\,}``

#14-b
Calculate the total time taken in forming 10 cm of ice. Assume that the temperature of the entire water reaches 0°C before the ice starts forming. Density of water = 1000 kg m^-3, latent heat of fusion of ice = 3.36 × 10⁵ J kg^-1 and thermal conductivity of ice = 1.7 W m^-1°C^-1. Neglect the expansion of water of freezing.
Ans : To form a thin ice layer of thickness dx, let the required be dt.
Mass of that thin layer, dm = A dx ρ_ω
Heat absorbed by that thin layer, dQ = Ldm
`` \frac{d\,\mathrm{\,Q\,}}{dt}=\frac{K·A\left(∆T\right)}{x}``
`` \frac{L\,\mathrm{\,d\,}m}{\,\mathrm{\,d\,}t}=\frac{KA\left(∆T\right)}{x}``
`` \frac{\left(\,\mathrm{\,A\,}dx{\,\mathrm{\,\rho \,}}_{w}\right)L}{\,\mathrm{\,d\,}t}=\frac{KA\mathit{∆}T}{x}``
`` \Rightarrow \underset{0}{\overset{t}{\int }}\,\mathrm{\,d\,}t=\frac{{\rho }_{w}L}{K\left(\Delta T\right)}\underset{0}{\overset{0.1}{\int }}xdx``
`` \Rightarrow t=\frac{{\rho }_{w}L}{K\left(\Delta T\right)}{\left[\frac{{x}^{2}}{2}\right]}_{0}^{0.1}``
`` t=\frac{{\rho }_{w}L}{K\left(\Delta T\right)}\times \left(\frac{{\left(0.1\right)}^{2}}{2}\right)``
`` t=\frac{{10}^{3}\times 3.36\times {10}^{5}\times 0.01}{1.7\times 10\times 2}``
`` t=\frac{3.36}{2\times 17}\times {10}^{6}\,\mathrm{\,sec\,}``
`` t=\frac{3.36}{2\times 17}\times \frac{{10}^{6}}{3600}\,\mathrm{\,hours\,}``
`` t=27.45\,\mathrm{\,hours\,}``
Page No 99:

Qstn #15
Consider the situation of the previous problem. Assume that the temperature of the water at the bottom of the lake remains constant at 4°C as the ice forms on the surface (the heat required to maintain the temperature of the bottom layer may come from the bed of the lake). The depth of the lake is 1.0 m. Show that the thickness of the ice formed attains a steady state maximum value. Find this value. The thermal conductivity of water = 0.50 W m^-1°C^-1. Take other relevant data from the previous problem.
Ans : Let the point upto which ice is formed is at a distance of x m from the top of the lake.
Under steady state, the rate of flow of heat from ice to this point should be equal to the rate flow of heat from water to this point.
Temperature of the top layer of ice = -10°C
Temperature of water at the bottom of the lake = 4°C
Temperature at the point upto which ice is formed = 0°C
`` {\left(\frac{\,\mathrm{\,\Delta \,}Q}{\,\mathrm{\,\Delta \,}t}\right)}_{\,\mathrm{\,ice\,}}={\left(\frac{\,\mathrm{\,\Delta \,}Q}{\,\mathrm{\,\Delta \,}t}\right)}_{\,\mathrm{\,water\,}}``
`` \frac{{K}_{\,\mathrm{\,ice\,}}}{{\displaystyle \frac{x}{\,\mathrm{\,A\,}\times 10}}}=\frac{{K}_{\,\mathrm{\,water\,}}}{{\displaystyle \frac{1-x}{\,\mathrm{\,A\,}\times 4}}}``
`` \frac{1.7\times 10}{x}=\frac{0.5\times 4}{1-x}``
`` \frac{17}{x}=\frac{2}{1-x}``
`` 17-17x=2x``
`` \Rightarrow x=\frac{17}{19}=0.89\,\mathrm{\,m\,}``
`` \Rightarrow x=89\,\mathrm{\,cm\,}``
Page No 99:

Qstn #16
Three rods of lengths 20 cm each and area of cross section 1 cm² are joined to form a triangle ABC. The conductivities of the rods are K_AB = 50 J s^-1 m^-1°C^-1, K_BC = 200 J s^-1 m^-1°C^-1 and K_AC = 400 J s^-1 m^-1°C^-1. The junctions A, B and C are maintained at 40°C, 80°C and 80°C respectively. Find the rate of heat flowing through the rods AB, AC and BC.
Ans : Thermal conductivity of rod AB, K_AB = 50 J/m-s-°C
Temperature of junction at A, T_A = 40°C
Thermal conductivity of rod BC, K_BC = 200 J/m-s-°C
Temperature of junction at B, T_B= 80°C
Thermal conductivity of rod BC, K_CA = 400 J/m-s-°C
Temperature of junction at C, T_C = 80°C
l = 20 cm = 20 × 10^-2 m
A = 1 cm² = 10^-4 m²
(a) `` \frac{{\left(\,\mathrm{\,\Delta \,}Q\right)}_{\,\mathrm{\,AB\,}}}{\,\mathrm{\,\Delta \,}t}=\frac{{K}_{\,\mathrm{\,AB\,}}A\left({T}_{\,\mathrm{\,B\,}}-{T}_{\,\mathrm{\,A\,}}\right)}{l}``
`` =\frac{50\times 1\times {10}^{-4}\left(40\right)}{20\times {10}^{-2}}``
`` =1\,\mathrm{\,W\,}``
(b) `` \frac{{\left(\,\mathrm{\,\Delta \,}Q\right)}_{\,\mathrm{\,AC\,}}}{\,\mathrm{\,\Delta \,}t}=\frac{{K}_{\,\mathrm{\,AC\,}}\mathit{·}A\left({T}_{\,\mathrm{\,C\,}}\mathit{-}{T}_{\,\mathrm{\,A\,}}\right)}{l}``
`` =\frac{400\times 1\times {10}^{-4}\times \left(40\right)}{20\times {10}^{-2}}``
`` =8\,\mathrm{\,W\,}``
(c) `` \frac{{\left(\,\mathrm{\,\Delta \,}Q\right)}_{\,\mathrm{\,BC\,}}}{\,\mathrm{\,\Delta \,}t}=\frac{\left({K}_{\,\mathrm{\,BC\,}}\right)A\left({T}_{\,\mathrm{\,B\,}}-{T}_{\,\mathrm{\,C\,}}\right)}{l}``
= 0
Page No 99:

Qstn #17
A semicircular rod is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the semicircular rod to the heat transferred through a cross section of the straight rod in a given time.
Ans :
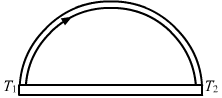
Let A be the area of cross section and K be the thermal conductivity of the material of the rod.
Let q₁ be the rate of flow of heat through a semicircular rod.
Rate of flow of heat is given by
`` {q}_{1}=\frac{dQ}{dt}=\frac{K\mathit{·}A\left({T}_{1}-{T}_{2}\right)}{\,\mathrm{\,\pi \,}r}``
Let q₂be the rate of flow of heat through a straight rod.
`` {q}_{2}=\frac{dQ}{dt}=\frac{KA\left({T}_{\mathit{1}}\mathit{-}{T}_{\mathit{2}}\right)}{2r}``
`` ``
Ratio of the rate of flow of heat through the 2 rods = `` \frac{{q}_{1}}{{q}_{2}}=\frac{2\,\mathrm{\,r\,}}{\,\mathrm{\,\pi \,}\,\mathrm{\,r\,}}=\frac{2}{\,\mathrm{\,\pi \,}}``
Page No 99:

Qstn #18
A metal rod of cross sectional area 1.0 cm² is being heated at one end. At one time, the temperatures gradient is 5.0°C cm^-1 at cross section A and is 2.5°C cm^-1 at cross section B. Calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB = 0.40 J°C^-1, thermal conductivity of the material of the rod = 200 W m^-1°C^-1. Neglect any loss of heat to the atmosphere
Ans :
Let the temperatures at the ends A and B be T_A and T_B, respectively.
Rate of flow of heat at end A of the rod is given by
`` \frac{{\,\mathrm{\,dQ\,}}_{\,\mathrm{\,A\,}}}{\,\mathrm{\,d\,}t}=K\,\mathrm{\,A\,}.\frac{\,\mathrm{\,d\,}}{\,\mathrm{\,d\,}l}\left({T}_{\,\mathrm{\,A\,}}\right)``
`` ``
`` ``
Rate of flow of heat at end B of the rod is given by
`` \frac{d{Q}_{\,\mathrm{\,B\,}}}{\,\mathrm{\,d\,}t}=K\,\mathrm{\,A\,}.\frac{\,\mathrm{\,d\,}}{\,\mathrm{\,d\,}l}\left({T}_{\,\mathrm{\,B\,}}\right)``
Heat absorbed by the rod = ms∆T
Here, s is the specific heat of the rod and ∆T is the temperature difference between ends A and B.
Rate of heat absorption by the rod is given by
`` \frac{\,\mathrm{\,d\,}Q}{\,\mathrm{\,d\,}t}=ms\frac{\,\mathrm{\,d\,}T}{\,\mathrm{\,d\,}t}``
`` \therefore ms\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}t}=K\,\mathrm{\,A\,}.\frac{{\,\mathrm{\,dT\,}}_{\,\mathrm{\,A\,}}}{\,\mathrm{\,d\,}l}-K\,\mathrm{\,A\,}.\frac{{\,\mathrm{\,dT\,}}_{\,\mathrm{\,B\,}}}{\,\mathrm{\,d\,}l}``
`` \Rightarrow \left(0.4\right).\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}t}=200\times 1\times {10}^{-4}\left(5-2.5\right)``
`` \frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}t}=12.5°\,\mathrm{\,C\,}/\,\mathrm{\,sec\,}``
Page No 99:

Qstn #19
Steam at 120°C is continuously passed through a 50 cm long rubber tube of inner and outer radii 1.0 cm and 1.2 cm. The room temperature is 30°C. Calculate the rate of heat flow through the walls of the tube. Thermal conductivity of rubber = 0.15 J s^-1 m^-1°C^-1.
Ans :
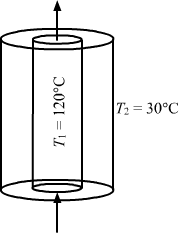
Inner radii = r = 1 cm = 10^-2 m
Outer radii = R = 1.2 cm = 1.2 × 10^-2 m
Length of the tube, l = 50 cm = 0.5 m
Thermal conductivity, k = 0.15 Js^-1 m^-1 °C^-1
Top View

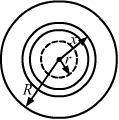
Let us consider a cylindrical shell of length l, radius x and thickness dx.
Rate of flow of heat q`` =\frac{d\,\mathrm{\,Q\,}}{dt}``
`` \frac{dQ}{dt}=\frac{-KA∆T}{dx}``
Here, the negative sign indicates that the rate of heat flow decreases as x increases.
`` q=-K\left(2\,\mathrm{\,\pi \,}xl\right).\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}x}``
`` {\int }_{r}^{R}\frac{\,\mathrm{\,d\,}x}{x}=-\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}dT``
`` {\left[\,\mathrm{\,ln\,}\left(x\right)\right]}_{r}^{R}=-\frac{2\,\mathrm{\,\pi K\,}l}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
`` \Rightarrow q=\frac{2\,\mathrm{\,\pi \,}kl\left({T}_{1}-{T}_{2}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{R}{r}}\right)}``
`` q=\frac{2\,\mathrm{\,\pi \,}\times 0.15\times 0.5\left(90\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{1.2\times {10}^{-2}}{1\times {10}^{-2}}}\right)}``
`` q=262.9\,\mathrm{\,J\,}/\,\mathrm{\,sec\,}``
Page No 99:

Qstn #20
A hole of radius r₁ is made centrally in a uniform circular disc of thickness d and radius r₂. The inner surface (a cylinder a length d and radius r₁) is maintained at a temperature θ₁ and the outer surface (a cylinder of length d and radius r₂) is maintained at a temperature θ₂ (θ₁ > θ₂). The thermal conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.
Ans :
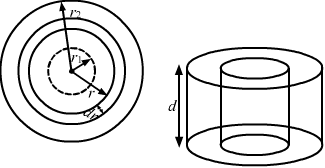
Let `` \frac{d\theta }{dt}`` be the rate of flow of heat.
Consider an annular ring of radius r and thickness dr.
Rate of flow of heat is given by
`` \frac{\,\mathrm{\,d\theta \,}}{\,\mathrm{\,d\,}t}=-K\left(2\,\mathrm{\,\pi \,}rd\right).\frac{\,\mathrm{\,d\theta \,}}{\,\mathrm{\,d\,}r}``
`` ``
Rate of flow of heat is constant.
∴ `` \frac{\,\mathrm{\,d\theta \,}}{\,\mathrm{\,d\,}t}=i``
`` i=-K\left(2\,\mathrm{\,\pi \,}r.d\right)\frac{\,\mathrm{\,d\theta \,}}{\,\mathrm{\,d\,}r}``
`` {\int }_{{r}_{1}}^{{r}_{2}}\frac{\,\mathrm{\,d\,}r}{r}=-\frac{2Kd}{i}{\int }_{{\theta }_{1}}^{{\theta }_{2}}d\,\mathrm{\,\theta \,}``
`` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{r}_{1}}^{{r}_{2}}=-\frac{2\,\mathrm{\,\pi \,}Kd}{i}\left[{\theta }_{2}-{\theta }_{1}\right]``
`` i=\frac{2\,\mathrm{\,\pi \,}Kd\left({\,\mathrm{\,\theta \,}}_{1}-{\,\mathrm{\,\theta \,}}_{2}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{r}_{2}}{{r}_{1}}}\right)}``
Page No 99:

Qstn #21
A hollow tube has a length l, inner radius R₁ and outer radius R₂. The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if

#21-a
the flat ends are maintained at temperature T₁ and T₂ (T₂ > T₁)
Ans : When the flat ends are maintained at temperatures T₁ and T₂ (where T₂ > T₁):
Area of cross section through which heat is flowing, `` \,\mathrm{\,A\,}=\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)``

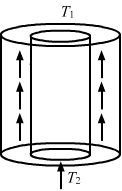
Rate of flow of heat`` =\frac{d\theta }{dt}``
`` =\frac{KA.∆T}{l}``
`` =\frac{K\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{l}``

#21-b
the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂.
Ans :
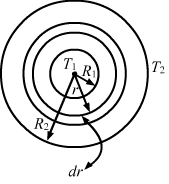
When the inside of the tube is maintained at temperature T₁ and the outside is maintained at T₂_:
Let us consider a cylindrical shell of radius r and thickness dr.
Rate of flow of heat, q`` =KA.\frac{d\,\mathrm{\,T\,}}{dr}``
`` q=KA.\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
`` q=K\left(2\,\mathrm{\,\pi \,}rl\right)\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
`` {\int }_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}\frac{dr}{r}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}d\,\mathrm{\,T\,}``
`` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left[{\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right]``
`` \,\mathrm{\,ln\,}\left(\frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}\right)=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
`` q=\frac{2\,\mathrm{\,\pi \,}Kl\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}}\right)}``
Page No 99:

Qstn #22
A composite slab is prepared by pasting two plates of thickness L₁ and L₂ and thermal conductivites K₁ and K₂. The slabs have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
Ans :
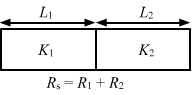
It is equivalent to the series combination of 2 resistors.
∴ R_S = R₁ +R₂
Resistance of a conducting slab, `` R=\frac{L}{KA}``
R_S = R₁ + R₂
`` \frac{{L}_{1}+{L}_{2}}{{K}_{\,\mathrm{\,s\,}}.A}=\frac{{L}_{1}}{{K}_{1}A}+\frac{{L}_{2}}{{K}_{2}A}``
`` \frac{{L}_{1}+{L}_{2}}{{K}_{\,\mathrm{\,S\,}}}=\frac{{L}_{1}}{{K}_{1}}+\frac{{L}_{2}}{{K}_{2}}``
`` \frac{{L}_{1}+{L}_{2}}{{K}_{\,\mathrm{\,S\,}}}=\frac{{L}_{1}{K}_{2}+{L}_{2}{K}_{1}}{{K}_{1}\times {K}_{2}}``
`` {K}_{\,\mathrm{\,S\,}}=\frac{\left({L}_{1}+{L}_{2}\right)\left({K}_{1}{K}_{2}\right)}{{L}_{1}{K}_{2}+{L}_{2}{K}_{1}}``
Page No 99:

Qstn #23
Figure (28-E2) shows a copper rod joined to a steel rod. The rods have equal length and equal cross sectional area. The free end of the copper rod is kept at 0°C and that of the steel rod is kept at 100°C. Find the temperature at the junction of the rods. Conductivity of copper = 390 W m^-1°C^-1 and that if steel = 46 W m^-1°C^-1.
Figure
Ans :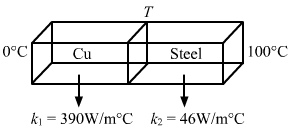
Rods are connected in series, so the rate of flow of heat is same.

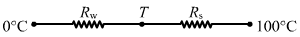
q₁ = q₂
Rate of flow of heat is given by
`` q=\frac{dQ}{dt}=\frac{\,\mathrm{\,Temperature\,}\,\mathrm{\,difference\,}}{\,\mathrm{\,Thermal\,}\,\mathrm{\,resistance\,}}``
As q₁ = q₂,
`` \Rightarrow \frac{T-0}{{R}_{\,\mathrm{\,cu\,}}}=\frac{100-T}{{R}_{\,\mathrm{\,S\,}}}``
`` A{K}_{1}\left(\frac{T-0}{l}\right)=\left(\frac{100-T}{l}\right){K}_{2}A``
`` \Rightarrow 390\,\mathrm{\,T\,}=\left(100-\,\mathrm{\,T\,}\right)46``
`` \Rightarrow \,\mathrm{\,T\,}=10.6°\,\mathrm{\,C\,}``
Page No 99:

Qstn #24
An aluminium rod and a copper rod of equal length 1.0 m and cross-sectional area 1 cm² are welded together as shown in figure (28-E3). One end is kept at a temperature of 20°C and the other at 60°C. Calculate the amount of heat taken out per second from the hot end. Thermal conductivity of aluminium = 200 W m^-1°C^-1 and of copper = 390 W m^-1°C^-1.
Figure
Ans :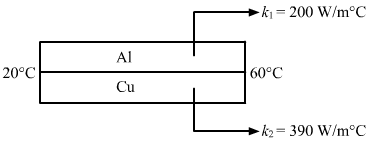

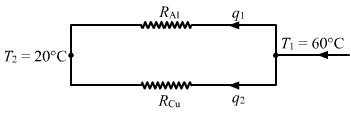
q₁ and q₂ are heat currents. In other words, they are the rates of flow of heat through aluminium and copper rod, respectively.
Applying KVL at the hot junction, we get
q = q₁ + q₂
Rate of heat flow, q = `` \frac{KA∆T}{l}``
As q = q₁ + q₂,
`` \frac{{K}_{\,\mathrm{\,P\,}}A\left({T}_{1}-{T}_{2}\right)}{l}=\frac{{K}_{1}A\left({T}_{1}-{T}_{2}\right)}{l}+\frac{{K}_{2}A\left({T}_{1}-{T}_{2}\right)}{l}``
`` Kp={K}_{1}+{K}_{2}``
`` =390+200=590\,\mathrm{\,W\,}/\,\mathrm{\,m\,}°\,\mathrm{\,C\,}``
`` \Rightarrow q=\frac{{K}_{P}A\left({T}_{1}-{T}_{2}\right)}{l}``
`` q=\frac{590\times {10}^{-4}\left(60-20\right)}{1}``
`` q=2.36\,\mathrm{\,W\,}``
Page No 100: