NEET-XII-Physics
28: Heat Transfer
- #17A semicircular rod is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the semicircular rod to the heat transferred through a cross section of the straight rod in a given time.Ans :
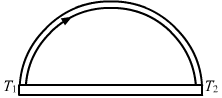
Let A be the area of cross section and K be the thermal conductivity of the material of the rod.
Let q1 be the rate of flow of heat through a semicircular rod.
Rate of flow of heat is given by
`` {q}_{1}=\frac{dQ}{dt}=\frac{K\mathit{·}A\left({T}_{1}-{T}_{2}\right)}{\,\mathrm{\,\pi \,}r}``
Let q2 be the rate of flow of heat through a straight rod.
`` {q}_{2}=\frac{dQ}{dt}=\frac{KA\left({T}_{\mathit{1}}\mathit{-}{T}_{\mathit{2}}\right)}{2r}``
`` ``
Ratio of the rate of flow of heat through the 2 rods = `` \frac{{q}_{1}}{{q}_{2}}=\frac{2\,\mathrm{\,r\,}}{\,\mathrm{\,\pi \,}\,\mathrm{\,r\,}}=\frac{2}{\,\mathrm{\,\pi \,}}``
Page No 99: