HomeLearn Fast select Course
Show Unit/ChapterChange UnitChange SubjectLast Menu
NEET-XII-Physics

28: Heat Transfer

with Solutions - page 4
Qstn# iv-21 Prvs-QstnNext-Qstn
  • #21
    A hollow tube has a length l, inner radius R1 and outer radius R2. The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2 (T2 > T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2. (a) the flat ends are maintained at temperature T1 and T2 (T2 > T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2.
    Ans : (a) When the flat ends are maintained at temperatures T1 and T2 (where T2 > T1):
    Area of cross section through which heat is flowing, `` \,\mathrm{\,A\,}=\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)``

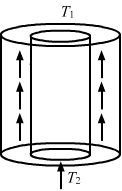
    ​Rate of flow of heat`` =\frac{d\theta }{dt}``
    `` =\frac{KA.∆T}{l}``
    `` =\frac{K\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{l}`` (b)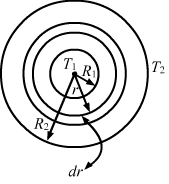
    When the inside of the tube is maintained at temperature T1 and the outside is maintained at T2:
    Let us consider a cylindrical shell of radius r and thickness dr.
    Rate of flow of heat, q`` =KA.\frac{d\,\mathrm{\,T\,}}{dr}``
    `` q=KA.\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
    `` q=K\left(2\,\mathrm{\,\pi \,}rl\right)\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
    `` {\int }_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}\frac{dr}{r}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}d\,\mathrm{\,T\,}``
    `` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left[{\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right]``
    `` \,\mathrm{\,ln\,}\left(\frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}\right)=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
    `` q=\frac{2\,\mathrm{\,\pi \,}Kl\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}}\right)}``
    Page No 99: (a) When the flat ends are maintained at temperatures T1 and T2 (where T2 > T1):
    Area of cross section through which heat is flowing, `` \,\mathrm{\,A\,}=\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)``

    ​Rate of flow of heat`` =\frac{d\theta }{dt}``
    `` =\frac{KA.∆T}{l}``
    `` =\frac{K\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{l}`` (b)
    When the inside of the tube is maintained at temperature T1 and the outside is maintained at T2:
    Let us consider a cylindrical shell of radius r and thickness dr.
    Rate of flow of heat, q`` =KA.\frac{d\,\mathrm{\,T\,}}{dr}``
    `` q=KA.\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
    `` q=K\left(2\,\mathrm{\,\pi \,}rl\right)\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
    `` {\int }_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}\frac{dr}{r}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}d\,\mathrm{\,T\,}``
    `` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left[{\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right]``
    `` \,\mathrm{\,ln\,}\left(\frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}\right)=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
    `` q=\frac{2\,\mathrm{\,\pi \,}Kl\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}}\right)}``
    Page No 99:
  • #21-a
    the flat ends are maintained at temperature T1 and T2 (T2 > T1)
    Ans : When the flat ends are maintained at temperatures T1 and T2 (where T2 > T1):
    Area of cross section through which heat is flowing, `` \,\mathrm{\,A\,}=\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)``

    ​Rate of flow of heat`` =\frac{d\theta }{dt}``
    `` =\frac{KA.∆T}{l}``
    `` =\frac{K\,\mathrm{\,\pi \,}\left({\,\mathrm{\,R\,}}_{2}^{2}-{\,\mathrm{\,R\,}}_{1}^{2}\right)\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{l}``
  • #21-b
    the inside of the tube is maintained at temperature T1 and the outside is maintained at T2.
    Ans :
    When the inside of the tube is maintained at temperature T1 and the outside is maintained at T2:
    Let us consider a cylindrical shell of radius r and thickness dr.
    Rate of flow of heat, q`` =KA.\frac{d\,\mathrm{\,T\,}}{dr}``
    `` q=KA.\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
    `` q=K\left(2\,\mathrm{\,\pi \,}rl\right)\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}r}``
    `` {\int }_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}\frac{dr}{r}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}d\,\mathrm{\,T\,}``
    `` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{\,\mathrm{\,R\,}}_{1}}^{{\,\mathrm{\,R\,}}_{2}}=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left[{\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right]``
    `` \,\mathrm{\,ln\,}\left(\frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}\right)=\frac{2\,\mathrm{\,\pi \,}Kl}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
    `` q=\frac{2\,\mathrm{\,\pi \,}Kl\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{\,\mathrm{\,R\,}}_{2}}{{\,\mathrm{\,R\,}}_{1}}}\right)}``
    Page No 99: