NEET-XII-Physics
28: Heat Transfer
- #19Steam at 120°C is continuously passed through a 50 cm long rubber tube of inner and outer radii 1.0 cm and 1.2 cm. The room temperature is 30°C. Calculate the rate of heat flow through the walls of the tube. Thermal conductivity of rubber = 0.15 J s-1 m-1°C-1.Ans :
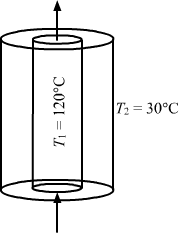
Inner radii = r = 1 cm = 10-2 m
Outer radii = R = 1.2 cm = 1.2 × 10-2 m
Length of the tube, l = 50 cm = 0.5 m
Thermal conductivity, k = 0.15 Js-1 m-1 °C-1
Top View
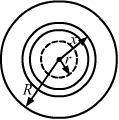
Let us consider a cylindrical shell of length l, radius x and thickness dx.
Rate of flow of heat q`` =\frac{d\,\mathrm{\,Q\,}}{dt}``
`` \frac{dQ}{dt}=\frac{-KA∆T}{dx}``
Here, the negative sign indicates that the rate of heat flow decreases as x increases.
`` q=-K\left(2\,\mathrm{\,\pi \,}xl\right).\frac{\,\mathrm{\,dT\,}}{\,\mathrm{\,d\,}x}``
`` {\int }_{r}^{R}\frac{\,\mathrm{\,d\,}x}{x}=-\frac{2\,\mathrm{\,\pi \,}Kl}{q}{\int }_{{\,\mathrm{\,T\,}}_{1}}^{{\,\mathrm{\,T\,}}_{2}}dT``
`` {\left[\,\mathrm{\,ln\,}\left(x\right)\right]}_{r}^{R}=-\frac{2\,\mathrm{\,\pi K\,}l}{q}\left({\,\mathrm{\,T\,}}_{2}-{\,\mathrm{\,T\,}}_{1}\right)``
`` \Rightarrow q=\frac{2\,\mathrm{\,\pi \,}kl\left({T}_{1}-{T}_{2}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{R}{r}}\right)}``
`` q=\frac{2\,\mathrm{\,\pi \,}\times 0.15\times 0.5\left(90\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{1.2\times {10}^{-2}}{1\times {10}^{-2}}}\right)}``
`` q=262.9\,\mathrm{\,J\,}/\,\mathrm{\,sec\,}``
Page No 99: