NEET-XII-Physics
28: Heat Transfer
- #20A hole of radius r1 is made centrally in a uniform circular disc of thickness d and radius r2. The inner surface (a cylinder a length d and radius r1) is maintained at a temperature θ1 and the outer surface (a cylinder of length d and radius r2) is maintained at a temperature θ2 (θ1 > θ2). The thermal conductivity of the material of the disc is K. Calculate the heat flowing per unit time through the disc.Ans :
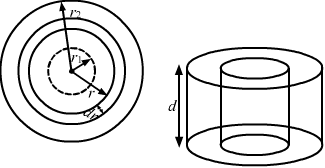
Let `` \frac{d\theta }{dt}`` be the rate of flow of heat.
Consider an annular ring of radius r and thickness dr.
Rate of flow of heat is given by
`` \frac{\,\mathrm{\,d\theta \,}}{\,\mathrm{\,d\,}t}=-K\left(2\,\mathrm{\,\pi \,}rd\right).\frac{\,\mathrm{\,d\theta \,}}{\,\mathrm{\,d\,}r}``
`` ``
Rate of flow of heat is constant.
∴ `` \frac{\,\mathrm{\,d\theta \,}}{\,\mathrm{\,d\,}t}=i``
`` i=-K\left(2\,\mathrm{\,\pi \,}r.d\right)\frac{\,\mathrm{\,d\theta \,}}{\,\mathrm{\,d\,}r}``
`` {\int }_{{r}_{1}}^{{r}_{2}}\frac{\,\mathrm{\,d\,}r}{r}=-\frac{2Kd}{i}{\int }_{{\theta }_{1}}^{{\theta }_{2}}d\,\mathrm{\,\theta \,}``
`` {\left[\,\mathrm{\,ln\,}\left(r\right)\right]}_{{r}_{1}}^{{r}_{2}}=-\frac{2\,\mathrm{\,\pi \,}Kd}{i}\left[{\theta }_{2}-{\theta }_{1}\right]``
`` i=\frac{2\,\mathrm{\,\pi \,}Kd\left({\,\mathrm{\,\theta \,}}_{1}-{\,\mathrm{\,\theta \,}}_{2}\right)}{\,\mathrm{\,ln\,}\left({\displaystyle \frac{{r}_{2}}{{r}_{1}}}\right)}``
Page No 99: