HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

17: Light Waves

with Solutions - page 7

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • #28-b
    Show that the intensity at P0 is three times the intensity due to any of the three slits individually.
    Figure
    Ans : To calculating the intensity at P0, consider the interference of light waves coming from all the three slits.
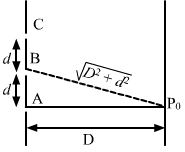
    Path difference of the wave fronts reaching from A and C is given by
    `` {\,\mathrm{\,CP\,}}_{0}-{\,\mathrm{\,AP\,}}_{0}=\sqrt{{D}^{2}+{\left(2d\right)}^{2}}-D``
    `` =\sqrt{{D}^{2}+\frac{8\lambda D}{3}}-D\left(\,\mathrm{\,Using\,}\,\mathrm{\,the\,}\,\mathrm{\,value\,}\,\mathrm{\,of\,}d\,\mathrm{\,from\,}\,\mathrm{\,part\,}a\right)``
    `` =D{\left\{1+\frac{8\lambda }{3D}\right\}}^{\frac{1}{2}}-D``
    `` \,\mathrm{\,Expanding\,}\,\mathrm{\,the\,}\,\mathrm{\,value\,}\,\mathrm{\,using\,}\,\mathrm{\,binomial\,}\,\mathrm{\,theorem\,}\,\mathrm{\,and\,}\,\mathrm{\,neglecting\,}\text{the}\,\mathrm{\,higher\,}\,\mathrm{\,order\,}\,\mathrm{\,terms\,},\,\mathrm{\,we\,}\,\mathrm{\,get\,}:``
    `` D\left\{1+\frac{1}{2}\times \frac{8\lambda }{3D}+...\right\}-D``
    `` ``
    `` {\,\mathrm{\,CP\,}}_{0}-{\,\mathrm{\,AP\,}}_{0}=\frac{4\,\mathrm{\,\lambda \,}}{3}``
    So, the corresponding phase difference between the wave fronts from A and C is given by
    `` {\varphi }_{c}=\frac{2\pi ∆{x}_{C}}{\lambda }=\frac{2\pi \times 4\lambda }{3\lambda }``
    `` \Rightarrow {\varphi }_{c}=\frac{8\pi }{3}\,\mathrm{\,or\,}\left(2\pi +\frac{2\pi }{3}\right)``
    `` \Rightarrow {\varphi }_{c}=\frac{2\pi }{3}...\left(1\right)``
    `` \,\mathrm{\,Again\,},{\varphi }_{\,\mathrm{\,B\,}}=\frac{2\pi ∆{x}_{B}}{\lambda }``
    `` \Rightarrow {\varphi }_{\,\mathrm{\,B\,}}=\frac{2\pi \lambda }{3\lambda }=\frac{2\pi }{3}...\left(2\right)``
    So, it can be said that light from B and C are in the same phase, as they have the same phase difference with respect to A.
    Amplitude of wave reaching P0 is given by
    `` A=\sqrt{{\left(2a\right)}^{2}+{a}^{2}+2a\times a\,\mathrm{\,cos\,}\left(\frac{2\pi }{3}\right)}``
    `` =\sqrt{4{a}^{2}+{a}^{2}+2{a}^{2}\sqrt{3}}``
    `` \therefore {l}_{po}=\,\mathrm{\,K\,}{\left(\sqrt{3}r\right)}^{2}=3\,\mathrm{\,K\,}{r}^{2}=3l``
    Here, I is the intensity due to the individual slits and Ipo is the total intensity at P0.
    Thus, the resulting amplitude is three times the intensity due to the individual slits.

    Page No 382:
  • Qstn #29
    In a Young’s double slit experiment, the separation between the slits = 2⋅0 mm, the wavelength of the light = 600 nm and the distance of the screen from the slits = 2⋅0 m. If the intensity at the centre of the central maximum is 0⋅20 W m-2, what will be the intensity at a point 0⋅5 cm away from this centre along the width of the fringes?
    Ans : Given:
    Separation between the slits, `` d=2\,\mathrm{\,mm\,}=2\times {10}^{-3}\,\mathrm{\,m\,}``
    `` ``
    Wavelength of the light, `` \lambda =600\,\mathrm{\,nm\,}=6\times {10}^{-7}\,\mathrm{\,m\,}``
    Distance of the screen from the slits, D = 2â‹…0 m
    `` {I}_{\,\mathrm{\,max\,}}=0.20\,\mathrm{\,W\,}/{\,\mathrm{\,m\,}}^{2}``
    `` \,\mathrm{\,For\,}\,\mathrm{\,the\,}\,\mathrm{\,point\,}\,\mathrm{\,at\,}\,\mathrm{\,a\,}\,\mathrm{\,position\,}y=0.5\,\mathrm{\,cm\,}=0.5\times {10}^{-2}\,\mathrm{\,m\,},``
    `` \text{p}\,\mathrm{\,ath\,}\,\mathrm{\,difference\,},∆x=\frac{yd}{D}.``
    `` \Rightarrow ∆x=\frac{0.5\times {10}^{-2}\times 2\times {10}^{-3}}{2}``
    `` =5\times {10}^{-6}\,\mathrm{\,m\,}``
    So, the corresponding phase difference is given by
    `` ∆\varphi =\frac{2\pi ∆x}{\lambda }=\frac{2\pi \times 5\times {10}^{-6}}{6\times {10}^{-7}}``
    `` =\frac{50\pi }{3}=16\pi +\frac{2\pi }{3}``
    `` \,\mathrm{\,or\,}∆\,\mathrm{\,\varphi \,}=\frac{2\pi }{3}``
    So, the amplitude of the resulting wave at point y = 0.5 cm is given by
    `` A=\sqrt{{a}^{2}+{a}^{2}+2{a}^{2}\,\mathrm{\,cos\,}\left(\frac{2\pi }{3}\right)}``
    `` =\sqrt{{a}^{2}+{a}^{2}-{a}^{2}}=a``
    `` ``
    Similarly, the amplitude of the resulting wave at the centre is 2a.
    Let the intensity of the resulting wave at point y = 0.5 cm be I.
    `` \,\mathrm{\,Since\,}\frac{I}{{I}_{\,\mathrm{\,max\,}}}=\frac{{A}^{2}}{{\left(2a\right)}^{2}},\,\mathrm{\,we\,}\,\mathrm{\,have\,}:``
    `` \frac{I}{0.2}=\frac{{A}^{2}}{4{a}^{2}}=\frac{{a}^{2}}{4{a}^{2}}``
    `` \Rightarrow I=\frac{0.2}{4}=0.05\,\mathrm{\,W\,}/{\,\mathrm{\,m\,}}^{2}``
    Thus, the intensity at a point 0.5 cm away from the centre along the width of the fringes is 0.05 W/m2.
    Page No 382:
  • Qstn #30
    In a Young’s double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength
    λ. Find the distance from the central point where the intensity falls to
    Ans : Given:
    Separation between the two slits = d
    Wavelength of the light = `` \lambda ``
    Distance of the screen = `` D``
  • #30-a
    half the maximum,
    Ans : When the intensity is half the maximum:
    Let Imax be the maximum intensity and I be the intensity at the required point at a distance y from the central point.
    So, `` I={a}^{2}+{a}^{2}+2{a}^{2}\,\mathrm{\,cos\,}\varphi ``
    Here, `` \varphi `` is the phase difference in the waves coming from the two slits.
    So, `` I=4{a}^{2}{\,\mathrm{\,cos\,}}^{2}\left(\frac{\varphi }{2}\right)``
    `` \Rightarrow \frac{I}{{I}_{\,\mathrm{\,max\,}}}=\frac{1}{2}``
    `` \Rightarrow \frac{4{a}^{2}{\,\mathrm{\,cos\,}}^{2}\left({\displaystyle \frac{\varphi }{2}}\right)}{4{a}^{2}}=\frac{1}{2}``
    `` \Rightarrow {\,\mathrm{\,cos\,}}^{2}\left(\frac{\varphi }{2}\right)=\frac{1}{2}``
    `` \Rightarrow \,\mathrm{\,cos\,}\left(\frac{\varphi }{2}\right)=\frac{1}{\sqrt{2}}``
    `` \Rightarrow \frac{\,\mathrm{\,\varphi \,}}{2}=\frac{\,\mathrm{\,\pi \,}}{4}``
    `` \Rightarrow \varphi =\frac{\,\mathrm{\,\pi \,}}{2}``
    `` \,\mathrm{\,Corrosponding\,}\,\mathrm{\,path\,}\,\mathrm{\,difference\,},∆x=\frac{\lambda }{4}``
    `` \Rightarrow y=\frac{∆xD}{d}=\frac{\lambda D}{4d}``
  • #30-b
    one-fourth the maximum.
    Ans : When the intensity is one-fourth of the maximum:
    `` \frac{I}{{I}_{\,\mathrm{\,max\,}}}=\frac{1}{4}``
    `` \Rightarrow 4{a}^{2}{\,\mathrm{\,cos\,}}^{2}\left(\frac{\varphi }{2}\right)=\frac{1}{4}``
    `` \Rightarrow {\,\mathrm{\,cos\,}}^{2}\left(\frac{\varphi }{2}\right)=\frac{1}{4}``
    `` \Rightarrow \,\mathrm{\,cos\,}\left(\frac{\varphi }{2}\right)=\frac{1}{2}``
    `` \Rightarrow \frac{\varphi }{2}=\frac{\pi }{3}``
    `` \,\mathrm{\,So\,},\,\mathrm{\,corrosponding\,}\,\mathrm{\,path\,}\,\mathrm{\,difference\,},∆x=\frac{\lambda }{3}``
    `` \,\mathrm{\,and\,}\,\mathrm{\,position\,},y=\frac{∆xD}{d}=\frac{\lambda D}{3d}.``
    Page No 382:
  • Qstn #31
    In a Young’s double slit experiment,
    λ=500 nm, d=1·0 mm and D=1·0 m. Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
    Ans : Given:
    Separation between the two slits, `` d=1\,\mathrm{\,mm\,}={10}^{-3}\,\mathrm{\,m\,}``
    `` ``
    Wavelength of the light, `` \lambda =500\,\mathrm{\,nm\,}=5\times {10}^{-7}\,\mathrm{\,m\,}``
    `` ``
    Distance of the screen, `` D=1\,\mathrm{\,m\,}``
    `` ``
    Let Imax be the maximum intensity and I be the intensity at the required point at a distance y from the central point.
    So, `` I={a}^{2}+{a}^{2}+2{a}^{2}\,\mathrm{\,cos\,}\varphi ``
    Here, `` \varphi `` is the phase difference in the waves coming from the two slits.
    So, `` I=4{a}^{2}{\,\mathrm{\,cos\,}}^{2}\left(\frac{\varphi }{2}\right)``
    `` \Rightarrow \frac{I}{{I}_{\,\mathrm{\,max\,}}}=\frac{1}{2}``
    `` \Rightarrow \frac{4{a}^{2}{\,\mathrm{\,cos\,}}^{2}\left({\displaystyle \frac{\varphi }{2}}\right)}{4{a}^{2}}=\frac{1}{2}``
    `` \Rightarrow {\,\mathrm{\,cos\,}}^{2}\left(\frac{\varphi }{2}\right)=\frac{1}{2}``
    `` \Rightarrow \,\mathrm{\,cos\,}\left(\frac{\varphi }{2}\right)=\frac{1}{\sqrt{2}}``
    `` \Rightarrow \frac{\,\mathrm{\,\varphi \,}}{2}=\frac{\,\mathrm{\,\pi \,}}{4}``
    `` \Rightarrow \varphi =\frac{\,\mathrm{\,\pi \,}}{2}``
    `` \,\mathrm{\,Corrosponding\,}\,\mathrm{\,path\,}\,\mathrm{\,difference\,},∆x=\frac{1}{4}``
    `` \Rightarrow y=\frac{∆xD}{d}=\frac{\lambda D}{4d}``
    `` \Rightarrow y=\frac{5\times {10}^{-7}\times 1}{4\times {10}^{-3}}``
    `` =1.25\times {10}^{-4}\,\mathrm{\,m\,}``
    ∴ The required minimum distance from the central maximum is `` 1.25\times {10}^{-4}\,\mathrm{\,m\,}``.
    Page No 382:
  • Qstn #32
    The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young’s double slit experiment in terms of
    λ, d and D where the symbols have their usual meanings.
    Ans : Given:
    Separation between two slits = d
    Wavelength of the light = `` \lambda ``
    `` ``
    Distance of the screen = `` D``
    Let Imax be the maximum intensity and I be half the maximum intensity at a point at a distance y from the central point.
    So, `` I={a}^{2}+{a}^{2}+2{a}^{2}\,\mathrm{\,cos\,}\varphi ``
    Here, `` \varphi `` is the phase difference in the waves coming from the two slits.
    So, `` I=4{a}^{2}{\,\mathrm{\,cos\,}}^{2}\left(\frac{\varphi }{2}\right)``
    `` \Rightarrow \frac{I}{{I}_{\,\mathrm{\,max\,}}}=\frac{1}{2}``
    `` \Rightarrow \frac{4{a}^{2}{\,\mathrm{\,cos\,}}^{2}\left({\displaystyle \frac{\varphi }{2}}\right)}{4{a}^{2}}=\frac{1}{2}``
    `` \Rightarrow {\,\mathrm{\,cos\,}}^{2}\left(\frac{\varphi }{2}\right)=\frac{1}{2}``
    `` \Rightarrow \,\mathrm{\,cos\,}\left(\frac{\varphi }{2}\right)=\frac{1}{\sqrt{2}}``
    `` \Rightarrow \frac{\,\mathrm{\,\varphi \,}}{2}=\frac{\,\mathrm{\,\pi \,}}{4}``
    `` \Rightarrow \varphi =\frac{\,\mathrm{\,\pi \,}}{2}``
    `` \,\mathrm{\,Corrosponding\,}\,\mathrm{\,path\,}\,\mathrm{\,difference\,},∆x=\frac{1}{4}``
    `` \Rightarrow y=\frac{∆xD}{d}=\frac{\lambda D}{4d}``
    The line-width of a bright fringe is defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum.
    So, line-width = 2y
    `` =2\frac{D\lambda }{4d}=\frac{D\lambda }{2d}``
    Thus, the required line width of the bright fringe is `` \frac{D\lambda }{2d}``.
    Page No 383:
  • Qstn #33
    Consider the situation shown in the figure. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen ∑1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen ∑2 is placed a further distance D away from ∑1. Find the ratio of the maximum to minimum intensity observed on ∑2 if z is equal to
    Ans : Given:
    Separation between the two slits = d
    Wavelength of the light =`` \lambda ``
    Distance of the screen = `` D``
    The fringe width (β) is given by `` \beta =\frac{\lambda D}{d}``.
    At S3, the path difference is zero. So, the maximum intensity occurs at amplitude = 2a.
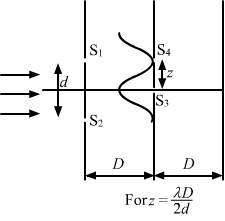
  • #33-a
    z=λD2d
    Ans : When `` z=\frac{D\lambda }{2d}``:
    The first minima occurs at S4, as shown in figure
    (a).
    With amplitude = 0 on screen ∑2, we get:
    `` \frac{{l}_{max}}{{l}_{min}}=\frac{{\left(2a+0\right)}^{2}}{{\left(2a-0\right)}^{2}}=1``
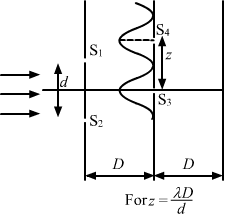
  • #33-b
    λDd
    Ans : When `` z=\frac{D\lambda }{d}``:
    The first maxima occurs at S4, as shown in the figure.

    With amplitude = `` 2a`` on screen ∑2, we get:
    `` \frac{{l}_{\,\mathrm{\,max\,}}}{{l}_{\,\mathrm{\,min\,}}}=\frac{{\left(2a+2a\right)}^{2}}{{\left(2a-2a\right)}^{2}}=\infty ``
    `` ``
  • #33-c
    λD4dFigure
    Ans : When `` z=\frac{D\lambda }{4d}``:

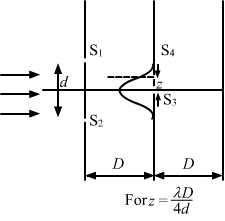
    The slit S4 falls at the mid-point of the central maxima and the first minima, as shown in the figure.
    `` \,\mathrm{\,Intensity\,}=\frac{{l}_{\,\mathrm{\,max\,}}}{2}``
    `` \Rightarrow \,\mathrm{\,Amplitude\,}=\sqrt{2}a``
    `` \therefore \frac{{l}_{\,\mathrm{\,max\,}}}{{l}_{\,\mathrm{\,min\,}}}=\frac{{\left(2a+\sqrt{2}a\right)}^{2}}{{\left(2a-\sqrt{2}a\right)}^{2}}=34``
    Page No 383:
  • Qstn #34
    Consider the arrangement shown in the figure (17-E7). By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When
    z=Dλ2d, the intensity measured at P is I. Find the intensity when z is equal to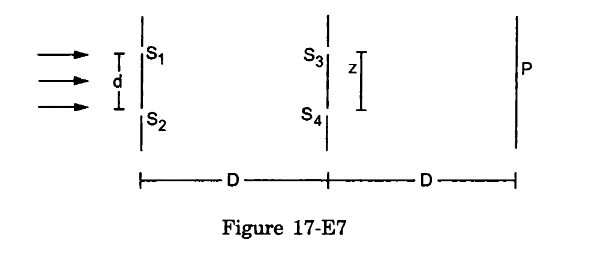
    Ans : Given:
    Fours slits S1, S2, S3 and S4.
    The separation between slits S3 and S4 can be changed.
    Point P is the common perpendicular bisector of S1S2 and S3S4.
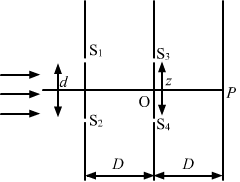
  • #34-a
    Dλd,
    Ans : `` \,\mathrm{\,For\,}z=\frac{\lambda D}{d}``:
    The position of the slits from the central point of the first screen is given by
    `` y={\,\mathrm{\,OS\,}}_{3}={\,\mathrm{\,OS\,}}_{4}=\frac{z}{2}=\frac{\lambda D}{2d}``
    `` ``
    `` ``
    The corresponding path difference in wave fronts reaching S3 is given by
    `` ∆x=\frac{yd}{D}=\frac{\lambda D}{2d}\times \frac{d}{D}=\frac{\lambda }{2}``
    Similarly at S4, path difference, `` ∆x=\frac{yd}{D}=\frac{\lambda D}{2d}\times \frac{d}{D}=\frac{\lambda }{2}``
    `` \,\mathrm{\,i\,}.\,\mathrm{\,e\,}.\,\mathrm{\,dark\,}\,\mathrm{\,fringes\,}\,\mathrm{\,are\,}\,\mathrm{\,formed\,}\,\mathrm{\,at\,}{\,\mathrm{\,S\,}}_{3}\,\mathrm{\,and\,}{\,\mathrm{\,S\,}}_{4}``
    `` ``.
    So, the intensity of light at S3 and S4 is zero. Hence, the intensity at P is also zero.
  • #34-b
    3Dλ2d and
    Ans : `` \,\mathrm{\,For\,}z=\frac{3\lambda D}{2d}``
    The position of the slits from the central point of the first screen is given by
    `` y={\,\mathrm{\,OS\,}}_{3}={\,\mathrm{\,OS\,}}_{4}=\frac{z}{2}=\frac{3\lambda D}{4d}``
    `` ``
    `` ``
    The corresponding path difference in wave fronts reaching S3 is given by
    `` ∆x=\frac{yd}{D}=\frac{3\lambda D}{4d}\times \frac{d}{D}=\frac{3\lambda }{4}``
    Similarly at S4, path difference, `` ∆x=\frac{yd}{D}=\frac{3\lambda D}{4d}\times \frac{d}{D}=\frac{3\lambda }{4}``
    Hence, the intensity at P is I.
  • #34-c
    2Dλd.
    Ans : Similarly, for `` z=\frac{2D\lambda }{d}``,
    the intensity at P is 2I.
    Page No 383:
next page