NEET-XII-Physics
17: Light Waves
- #33Consider the situation shown in the figure. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen ∑1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen ∑2 is placed a further distance D away from ∑1. Find the ratio of the maximum to minimum intensity observed on ∑2 if z is equal to (a) z=λD2d (b) λDd (c) λD4dFigure (a) z=λD2d (b) λDd (c) λD4dFigureAns : Given:
Separation between the two slits = d
Wavelength of the light =`` \lambda ``
Distance of the screen = `` D``
The fringe width (β) is given by `` \beta =\frac{\lambda D}{d}``.
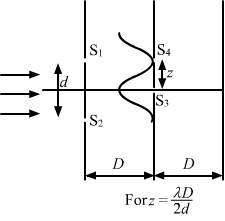
At S3, the path difference is zero. So, the maximum intensity occurs at amplitude = 2a. (a) When `` z=\frac{D\lambda }{2d}``:
The first minima occurs at S4, as shown in figure
(a).
With amplitude = 0 on screen ∑2, we get:
`` \frac{{l}_{max}}{{l}_{min}}=\frac{{\left(2a+0\right)}^{2}}{{\left(2a-0\right)}^{2}}=1``
 (b) When `` z=\frac{D\lambda }{d}``:
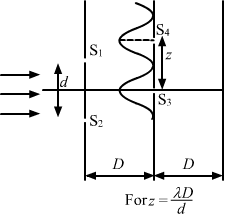
(b) When `` z=\frac{D\lambda }{d}``:
The first maxima occurs at S4, as shown in the figure.
With amplitude = `` 2a`` on screen ∑2, we get:
`` \frac{{l}_{\,\mathrm{\,max\,}}}{{l}_{\,\mathrm{\,min\,}}}=\frac{{\left(2a+2a\right)}^{2}}{{\left(2a-2a\right)}^{2}}=\infty ``
`` `` (c) When `` z=\frac{D\lambda }{4d}``:
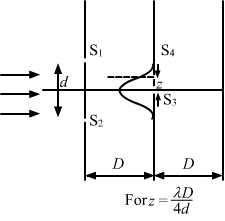
The slit S4 falls at the mid-point of the central maxima and the first minima, as shown in the figure.
`` \,\mathrm{\,Intensity\,}=\frac{{l}_{\,\mathrm{\,max\,}}}{2}``
`` \Rightarrow \,\mathrm{\,Amplitude\,}=\sqrt{2}a``
`` \therefore \frac{{l}_{\,\mathrm{\,max\,}}}{{l}_{\,\mathrm{\,min\,}}}=\frac{{\left(2a+\sqrt{2}a\right)}^{2}}{{\left(2a-\sqrt{2}a\right)}^{2}}=34``
Page No 383: (a) When `` z=\frac{D\lambda }{2d}``:
The first minima occurs at S4, as shown in figure
(a).
With amplitude = 0 on screen ∑2, we get:
`` \frac{{l}_{max}}{{l}_{min}}=\frac{{\left(2a+0\right)}^{2}}{{\left(2a-0\right)}^{2}}=1``
 (b) When `` z=\frac{D\lambda }{d}``:
(b) When `` z=\frac{D\lambda }{d}``:
The first maxima occurs at S4, as shown in the figure.

With amplitude = `` 2a`` on screen ∑2, we get:
`` \frac{{l}_{\,\mathrm{\,max\,}}}{{l}_{\,\mathrm{\,min\,}}}=\frac{{\left(2a+2a\right)}^{2}}{{\left(2a-2a\right)}^{2}}=\infty ``
`` `` (c) When `` z=\frac{D\lambda }{4d}``:

The slit S4 falls at the mid-point of the central maxima and the first minima, as shown in the figure.
`` \,\mathrm{\,Intensity\,}=\frac{{l}_{\,\mathrm{\,max\,}}}{2}``
`` \Rightarrow \,\mathrm{\,Amplitude\,}=\sqrt{2}a``
`` \therefore \frac{{l}_{\,\mathrm{\,max\,}}}{{l}_{\,\mathrm{\,min\,}}}=\frac{{\left(2a+\sqrt{2}a\right)}^{2}}{{\left(2a-\sqrt{2}a\right)}^{2}}=34``
Page No 383:
- #33-az=λD2dAns : When `` z=\frac{D\lambda }{2d}``:
The first minima occurs at S4, as shown in figure
(a).
With amplitude = 0 on screen ∑2, we get:
`` \frac{{l}_{max}}{{l}_{min}}=\frac{{\left(2a+0\right)}^{2}}{{\left(2a-0\right)}^{2}}=1``

- #33-bλDdAns : When `` z=\frac{D\lambda }{d}``:
The first maxima occurs at S4, as shown in the figure.

With amplitude = `` 2a`` on screen ∑2, we get:
`` \frac{{l}_{\,\mathrm{\,max\,}}}{{l}_{\,\mathrm{\,min\,}}}=\frac{{\left(2a+2a\right)}^{2}}{{\left(2a-2a\right)}^{2}}=\infty ``
`` ``
- #33-cλD4dFigureAns : When `` z=\frac{D\lambda }{4d}``:

The slit S4 falls at the mid-point of the central maxima and the first minima, as shown in the figure.
`` \,\mathrm{\,Intensity\,}=\frac{{l}_{\,\mathrm{\,max\,}}}{2}``
`` \Rightarrow \,\mathrm{\,Amplitude\,}=\sqrt{2}a``
`` \therefore \frac{{l}_{\,\mathrm{\,max\,}}}{{l}_{\,\mathrm{\,min\,}}}=\frac{{\left(2a+\sqrt{2}a\right)}^{2}}{{\left(2a-\sqrt{2}a\right)}^{2}}=34``
Page No 383: