NEET-XII-Physics
07: Circular Motion
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #5If the horizontal force needed for the turn in the previous problem is to be supplied by the normal force by the road, what should be the proper angle of banking?Ans : Given:
Speed of the scooter = v = 36 km/hr = 10 m/s
Radius of turn = r = 30 m
Let the angle of banking be `` \theta ``. We have:
`` \,\mathrm{\,tan \,}\theta =\frac{{v}^{2}}{rg}``
`` \Rightarrow \,\mathrm{\,tan \,}\theta =\frac{100}{30\times 10}=\frac{1}{3}``
`` \Rightarrow \theta ={\,\mathrm{\,tan \,}}^{-1}\left(\frac{1}{3}\right)``
Page No 114:
- Qstn #6A park has a radius of 10 m. If a vehicle goes round it at an average speed of 18 km/hr, what should be the proper angle of banking?Ans : Given:
Speed of the vehicle = v = 18 km/h = 5 m/s
Radius of the park = r = 10 m
Let the angle of banking be `` \theta ``.
Thus, we have:
`` \,\mathrm{\,tan \,}\theta =\frac{{v}^{2}}{rg}``
`` \Rightarrow \theta ={\,\mathrm{\,tan \,}}^{-1}\left(\frac{25}{100}\right)``
`` \Rightarrow \theta ={\,\mathrm{\,tan \,}}^{-1}\left(\frac{1}{4}\right)``
Page No 114:
- Qstn #7If the road of the previous problem is horizontal (no banking), what should be the minimum friction coefficient so that scooter going at 18 km/hr does not skid?Ans : If the road is horizontal (no banking), we have:
`` \frac{m{v}^{2}}{R}={f}_{s}``
`` N=mg``
`` ``
Here, fs is the force of friction and N is the normal reaction.
If μ is the friction coefficient, we have:
`` \,\mathrm{\,Friction \,}\,\mathrm{\,force \,}={f}_{s}=\mu N``
`` \,\mathrm{\,So \,},\frac{m{v}^{2}}{R}=\mu mg``
Here,
Velocity = v = 5 m/s
Radius = R = 10 m
`` \therefore \frac{25}{10}=\mu g``
`` \Rightarrow \mu =\left(\frac{25}{100}\right)=0.25``
Page No 114:
- Qstn #8A circular road of radius 50 m has the angle of banking equal to 30°. At what speed should a vehicle go on this road so that the friction is not used?Ans : Given:
Angle of banking = θ = 30°
Radius = r = 50 m
Assume that the vehicle travels on this road at speed v so that the friction is not used.
We get:
`` \,\mathrm{\,tan \,}\theta =\frac{{v}^{2}}{rg}``
`` \Rightarrow \,\mathrm{\,tan \,}30°=\frac{{v}^{2}}{rg}``
`` \Rightarrow \frac{1}{\sqrt{3}}=\frac{{v}^{2}}{rg}``
`` \Rightarrow {v}^{2}=\frac{rg}{\sqrt{3}}=\frac{50\times 10}{\sqrt{3}}``
`` \Rightarrow v=\sqrt{\frac{500}{\sqrt{3}}}=17\,\mathrm{\,m \,}/\,\mathrm{\,s \,}``
Page No 114:
- Qstn #9In the Bohr model of hydrogen atom, the electron is treated as a particle going in a circle with the centre at the proton. The proton itself is assumed to be fixed in an inertial frame. The centripetal force is provided by the Coulomb attraction. In the ground state, the electron goes round the proton in a circle of radius 5.3 × 10-11 m. Find the speed of the electron in the ground state. Mass of the electron = 9.1 × 10-31 kg and charge of the electron = 1.6 × 10-19 C.Ans : `` \,\mathrm{\,Given \,}:``
`` \,\mathrm{\,Radius \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,orbit \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,ground \,}\,\mathrm{\,state \,}=r=5.3\times {10}^{-11}\,\mathrm{\,m \,}``
`` \,\mathrm{\,Mass \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,electron \,}=m=9.1\times {10}^{-31}\,\mathrm{\,kg \,}``
`` \,\mathrm{\,Charge \,}\,\mathrm{\,of \,}\,\mathrm{\,electron \,}=q=1.6\times {10}^{-19}\,\mathrm{\,c \,}``
`` \,\mathrm{\,We \,}\,\mathrm{\,know \,}:``
`` \,\mathrm{\,Centripetal \,}force=\,\mathrm{\,Coulomb \,}attraction``
`` \,\mathrm{\,Therefore \,},\,\mathrm{\,we \,}\,\mathrm{\,have \,}:``
`` \Rightarrow \frac{m{v}^{2}}{r}=\frac{1}{4{\,\mathrm{\,\pi \epsilon \,}}_{\circ }}\frac{{q}^{2}}{{r}^{2}}``
`` \Rightarrow {v}^{2}=\frac{1}{4{\,\mathrm{\,\pi \epsilon \,}}_{\circ }}\frac{{q}^{2}}{rm}``
`` =\frac{9\times {10}^{9}\times {\left(1.6\times {10}^{-19}\right)}^{2}}{5.3\times {10}^{-11}\times 9.1\times {10}^{-31}}``
`` =\frac{23.04}{48.23}\times {10}^{13}``
`` =0.477\times {10}^{13}=4.7\times {10}^{12}``
`` \Rightarrow v=\sqrt{4.7}\times {10}^{12}=2.2\times {10}^{6}\,\mathrm{\,m \,}/\,\mathrm{\,s \,}``
Page No 114:
- Qstn #10A stone is fastened to one end of a string and is whirled in a vertical circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.Ans : Let m be the mass of the stone.
Let v be the velocity of the stone at the highest point.
R is the radius of the circle.
Thus, in a vertical circle and at the highest point, we have:
`` \frac{m{v}^{2}}{R}=mg``
`` \Rightarrow {v}^{2}=Rg``
`` \Rightarrow v=\sqrt{Rg}``
Page No 114:
- Qstn #11A ceiling fan has a diameter (of the circle through the outer edges of the three blades) of 120 cm and rpm 1500 at full speed. Consider a particle of mass 1 g sticking at the outer end of a blade. How much force does it experience when the fan runs at full speed? Who exerts this force on the particle? How much force does the particle exert on the blade along its surface?Ans : Diameter of the fan = 120 cm
∴ Radius of the fan = r = 60 cm = 0.6 m
Mass of the particle = M = 1 g = 0.001 kg
Frequency of revolutions = n = 1500 rev/min = 25 rev/s
Angular velocity = ω = 2`` \pi ``n = 2`` \pi `` × 25 = 157.14 rev/s
Force of the blade on the particle:
F = Mrw2
= (0.001) × 0.6 × (157.14)2
=14.8 N
The moving fan exerts this force on the particle.
The particle also exerts a force of 14.8 N on the blade along its surface.
Page No 114:
- Qstn #12A mosquito is sitting on an L.P. record disc rotating on a turn table at
3313revolutions per minute. The distance of the mosquito from the centre of the turn table is 10 cm. Show that the friction coefficient between the record and the mosquito is greater than π2/81.Ans : `` \,\mathrm{\,Frequency \,}\,\mathrm{\,of \,}\,\mathrm{\,disc \,}=n=33\frac{1}{3}\,\mathrm{\,rev \,}/\,\mathrm{\,m \,}=\frac{100}{3\times 60}\,\mathrm{\,rev \,}/\,\mathrm{\,s \,}``
`` ``
`` \,\mathrm{\,Angular \,}\,\mathrm{\,velocity \,}=\,\mathrm{\,\omega \,}=2\,\mathrm{\,\pi \,}n=2\,\mathrm{\,\pi \,}\times \frac{100}{180}=\frac{10\,\mathrm{\,\pi \,}}{9}\,\mathrm{\,rad \,}/\,\mathrm{\,s \,}``
`` r=10\,\mathrm{\,cm \,}=0.1\,\mathrm{\,m \,}``
`` g=10\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
It is given that the mosquito is sitting on the L.P. record disc. Therefore, we have:
Friction force ≥ Centrifugal force on the mosquito
⇒ μmg ≥ mrω2
⇒ μ ≥ rω2/g
`` \Rightarrow \mu \ge \,\mathrm{\,0.1\times \,}{\left({\displaystyle \frac{\,\mathrm{\,10\pi \,}}{9}}\right)}^{2}\frac{1}{10}``
`` \Rightarrow \mu \ge \frac{{\,\mathrm{\,\pi \,}}^{2}}{81}``
Page No 114:
- Qstn #13A simple pendulum is suspended from the ceiling of a car taking a turn of radius 10 m at a speed of 36 km/h. Find the angle made by he string of the pendulum with the vertical if this angle does not change during the turn.Ans : Speed of the car = v = 36 km/hr = 10 m/s
Acceleration due to gravity = g = 10 m/s2
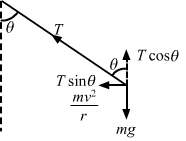
Let T be the tension in the string when the pendulum makes an angle θ with the vertical.
From the figure, we get:
`` T\,\mathrm{\,sin \,}\theta =\frac{m{v}^{2}}{r}...\left(\,\mathrm{\,i \,}\right)``
`` T\,\mathrm{\,cos \,}\theta =mg...\left(\,\mathrm{\,ii \,}\right)``
`` \Rightarrow \frac{\,\mathrm{\,sin \,}\theta }{\,\mathrm{\,cos \,}\theta }=\frac{m{v}^{2}}{rmg}``
`` \Rightarrow \,\mathrm{\,tan \,}\theta =\frac{{v}^{2}}{rg}``
`` \Rightarrow \theta ={\,\mathrm{\,tan \,}}^{-1}\left(\frac{{v}^{2}}{rg}\right)``
`` ={\,\mathrm{\,tan \,}}^{-1}\left[\frac{100}{(10\times 10)}\right]``
`` ={\,\mathrm{\,tan \,}}^{-1}\left(1\right)``
`` \Rightarrow \theta =45°``
Page No 115:
- Qstn #14The bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this instant.Ans :

Given:
Mass of the bob = m = 100 gm = 0.1 kg
Length of the string = r = 1 m
Speed of bob at the lowest point in its path = 1.4 m/s
Let T be the tension in the string.
From the free body diagram, we get:
`` T=mg+\frac{m{v}^{2}}{r}``
`` =\left(\frac{1}{10}\right)\times 9.8+\frac{(1.4{)}^{2}}{10}``
`` =0.98+0.196``
`` =1.176\approx 1.2\,\mathrm{\,N \,}``
`` ``
Page No 115:
- Qstn #15Suppose the bob of the previous problem has a speed of 1.4 m/s when the string makes an angle of 0.20 radian with the vertical. Find the tension at this instant. You can use cos θ ≈ 1 - θ2/2 and SINθ ≈ θ for small θ.Ans : Given:
Mass of the bob = m = 0.1 kg
Length of the circle = R = 1 m
Velocity of the bob = v = 1.4 m/s
Let T be the tension in the string when it makes an angle of 0.20 radian with the vertical.

From the free body diagram, we get:
`` T-mg\,\mathrm{\,cos \,}\theta =\frac{m{v}^{2}}{R}``
`` T=\frac{m{v}^{2}}{R}+mg\,\mathrm{\,cos \,}\theta ``
`` \,\mathrm{\,For \,}\,\mathrm{\,small \,}\,\mathrm{\,\theta \,},\,\mathrm{\,it \,}\,\mathrm{\,is \,}\,\mathrm{\,given \,}\,\mathrm{\,that \,}:``
`` \,\mathrm{\,cos \,}\theta =1-\frac{{\theta }^{2}}{2}``
`` \therefore T=\frac{0.1\times (1.4{)}^{2}}{1}+(0.1)\times 9.8\left(1-\frac{{\theta }^{2}}{2}\right)``
`` =0.196+0.98\times \left(1-\frac{{\left(0.2\right)}^{2}}{2}\right)``
`` =0.196+0.9604``
`` =1.156\,\mathrm{\,N \,}\approx 1.16\,\mathrm{\,N \,}``
Page No 115:
- Qstn #16Suppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.Ans : Let T be the tension in the string at the extreme position.
Velocity of the pendulum is zero at the extreme position.
So, there is no centripetal force on the bob.
∴ T = mgcosθ0

Page No 115:
- #17-aBy what friction is the dinbalance reag less than hits true weight?Ans : Balance reading = Normal force on the balance by the Earth.
At equator, the normal force (N) on the spring balance:
N = mg - mω2r
True weight = mg
Therefore, we have:
`` \,\mathrm{\,Fraction \,}\,\mathrm{\,less \,}\,\mathrm{\,than \,}\,\mathrm{\,the \,}\,\mathrm{\,true \,}\,\mathrm{\,weight \,}=\frac{mg-(mg-m{\,\mathrm{\,\omega \,}}^{2}r)}{mg}``
`` =\frac{{\,\mathrm{\,\omega \,}}^{2}r}{g}={\left(\frac{2\,\mathrm{\,\pi \,}}{24\times 3600}\right)}^{2}\left(\frac{6.4\times {10}^{6}}{10}\right)``
`` =3.5\times {10}^{-3}``
- #17-bIf the speed of earth’s rotation is increased by such an amount that the balance reading is half the true weight, what will be the length of the day in this case?Ans : When the balance reading is half, we have:
`` \,\mathrm{\,True \,}weight=\frac{mg-m{\,\mathrm{\,\omega \,}}^{2}r}{mg}=\frac{1}{2}``
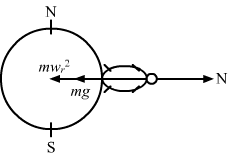
`` \Rightarrow {\,\mathrm{\,\omega \,}}^{2}r=\frac{g}{2}``
`` \Rightarrow \,\mathrm{\,\omega \,}=\sqrt{\frac{g}{2r}}``
`` =\sqrt{\frac{10}{2\times 6400\times {10}^{3}}}\,\mathrm{\,rad \,}/\,\mathrm{\,s \,}``
`` \therefore \,\mathrm{\,Duration \,}\,\mathrm{\,of \,}\,\mathrm{\,the \,}\,\mathrm{\,day \,}=2\pi \times \sqrt{\frac{2\times 6400\times {10}^{3}}{9.8}}\,\mathrm{\,s \,}``
`` =2\,\mathrm{\,\pi \,}\sqrt{\frac{6.4\times {10}^{7}}{49}}\,\mathrm{\,s \,}``
`` =\frac{2\,\mathrm{\,\pi \,}\times 8000}{7\times 3600}\,\mathrm{\,h \,}=2\,\mathrm{\,h \,}``
Page No 115: