NEET-XII-Physics
39: Alternating Current
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #14Can a hot-wire ammeter be used to measure a direct current of constant value? Do we have to change the graduations?Ans : A hot-wire ammeter measures the rms value of current for an alternating current. So, it can be used to measure the direct current of constant value because that constant value will be equal to the rms value of current. As, the rms value of the current is same as the direct current thus we need not change the graduations.
Page No 329:
- #Section : ii
- Qstn #1A capacitor acts as an infinite resistance for
(a) DC
(b) AC
(c) DC as well as AC
(d) neither AC nor DCdigAnsr: aAns : (a) DC
For a DC source, ω = 0. So, the reactance of the capacitance is given by,
`` {X}_{C}=\frac{1}{\omega C}=\frac{1}{0}=\infty ``
Page No 329:
- Qstn #2An AC source producing emf
ε = ε0 [cos (100 π s-1)t + cos (500 π s-1)t]
is connected in series with a capacitor and a resistor. The steady-state current in the circuit is found to be i = i1 cos [(100 π s-1)t + φ1) + i2 cos [(500π s-1)t + Ï•2]. So,
(a) i1 > i2
(b) i1 = i2
(c) i1 < i2
(d) The information is insufficient to find the relation between i1 and i2.digAnsr: cAns : (c) i1 < i2
The charge on the capacitor during steady state is given by,
`` Q=C\epsilon ={\epsilon }_{0}C\left[\,\mathrm{\,cos\,}\left(100{\,\mathrm{\,\pi s\,}}^{-1}\right)t+\,\mathrm{\,cos\,}\left(500{\,\mathrm{\,\pi s\,}}^{-1}\right)t\right]``
The steady state current is, thus, given by,
`` i=\frac{dQ}{dt}={\epsilon }_{0}C\times 100\,\mathrm{\,\pi \,}\left[\,\mathrm{\,sin\,}\left(100{\,\mathrm{\,\pi s\,}}^{-1}\right)t\right]+{\epsilon }_{\mathit{0}}C\times 500\,\mathrm{\,\pi \,}\left[\,\mathrm{\,sin\,}\left(500{\,\mathrm{\,\pi s\,}}^{-1}\right)t\right]``
`` \Rightarrow i=100C{\,\mathrm{\,\pi \epsilon \,}}_{0}\,\mathrm{\,cos\,}\left[\left(100{\,\mathrm{\,\pi s\,}}^{-1}\right)\,\mathrm{\,t\,}+{\varphi }_{1}\right]+500C{\,\mathrm{\,\pi \epsilon \,}}_{0}\,\mathrm{\,cos\,}\left[\left(500{\,\mathrm{\,\pi s\,}}^{-1}\right)+{\varphi }_{2}\right]``
`` \Rightarrow {i}_{1}=100C{\,\mathrm{\,\pi \epsilon \,}}_{0}\&{i}_{\mathit{2}}=500C{\,\mathrm{\,\pi \epsilon \,}}_{0}``
`` \therefore {i}_{2}>{i}_{1}``
Page No 329:
- Qstn #3The peak voltage of a 220 V AC source is
(a) 220 V
(b) about 160 V
(c) about 310 V
(d) 440 VdigAnsr: cAns : (c) about 310 V
Given:
Vrms = 220 V
The peak value of voltage is given by,
`` {V}_{p}=\sqrt{2}\times {V}_{rms}=1.414\times 220=311\,\mathrm{\,V\,}``
Page No 329:
- Qstn #4An AC source is rated 220 V, 50 Hz. The average voltage is calculated in a time interval of 0.01 s. It
(a) must be zero
(b) may be zero
(c) is never zero
(d)
is 220/2 VdigAnsr: bAns : (b) may be zero
Let the AC voltage be given by,
`` V={V}_{0}\,\mathrm{\,sin\,}\omega t``
Here, ω = 2`` \pi ``f = 314 rad/s
The average voltage over the given time,
`` {V}_{avg}=\frac{{\int }_{0}^{0.01}Vdt}{{\int }_{0}^{0.01}dt}=-{V}_{0}{\left[\frac{\,\mathrm{\,cos\,}\omega t}{\omega }\right]}_{0}^{0.01}``
`` =\frac{{V}_{0}}{\omega \times 0.01}\left(1-\,\mathrm{\,cos\,}\omega \left(0.01\right)\right)``
`` =\frac{{V}_{0}}{314\times 0.01}\left(1-\,\mathrm{\,cos\,}\left(314\times 0.01\right)\right)``
`` =\frac{{V}_{0}}{3.14}\left(1-\,\mathrm{\,cos\pi \,}\right)``
`` =\frac{2{V}_{0}}{\,\mathrm{\,\pi \,}}=140.127\,\mathrm{\,V\,}``
Also, when `` V={V}_{0}\,\mathrm{\,cos\,}\omega t``,
`` {V}_{avg}=\frac{{\int }_{0}^{0.01}Vdt}{{\int }_{0}^{0.01}dt}={V}_{0}{\left[\frac{\,\mathrm{\,sin\,}\omega t}{\omega }\right]}_{0}^{0.01}``
`` =\frac{{V}_{0}}{\omega \times 0.01}\left(\,\mathrm{\,sin\,}\omega \left(0.01\right)-0\right)``
`` =\frac{{V}_{0}}{314\times 0.01}\left(\,\mathrm{\,sin\,}\left(314\times 0.01\right)\right)``
`` =\frac{{V}_{0}}{3.14}\left(\,\mathrm{\,sin\,}\pi \right)``
`` =0``
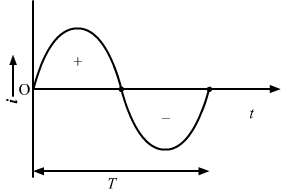
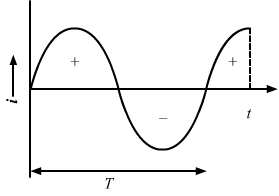
From the above results, we can say that the average voltage can be zero. But it is not necessary that it should be zero or never zero.
Page No 329:
- Qstn #5The magnetic field energy in an inductor changes from maximum to minimum value in 5.0 ms when connected to an AC source. The frequency of the source is
(a) 20 Hz
(b) 50 Hz
(c) 200 Hz
(d) 500 HzdigAnsr: bAns : (b) 50 Hz
The magnetic field energy in an inductor is given by,
`` E=\frac{1}{2}L{i}^{2}``
The magnetic energy will be maximum when the current will reach its peak value, i0, and it will be minimum when the current will become zero.
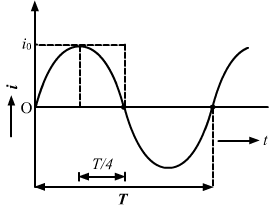
From the above graph of alternating current, we can see that current reduces from maximum to zero in T/4 time, where T is the time period.
So, in this case, T/4 = 5 ms
`` \Rightarrow T=20\,\mathrm{\,ms\,}``
`` \therefore \,\mathrm{\,Frequency\,},\nu =\frac{1}{T}=\frac{1}{20\times {10}^{-3}}=50\,\mathrm{\,Hz\,}``
Page No 329:
- Qstn #6Which of the following plots may represent the reactance of a series LC combination?
FigureAns : (d)
The reactance of a series LC circuit is given by,
`` X={X}_{L}-{X}_{C}=\omega L-\frac{1}{\omega C}``
`` \Rightarrow X=2\,\mathrm{\,\pi \,}fL-\frac{1}{2\,\mathrm{\,\pi \,}fC}``
The correct relation between the reactance and f is represented by the graph in option
(d).
`` X=0``, when `` {X}_{L}={X}_{C}``.
Thus plot d represent the reactance of a series LC combination.
Page No 329:
- Qstn #7A series AC circuit has a resistance of 4 Ω and a reactance of 3 Ω. The impedance of the circuit is
(a) 5 Ω
(b) 7 Ω
(c) 12/7 Ω
(d) 7/12 ΩdigAnsr: aAns : (a) 5 Ω
The impedance of the circuit is given by
`` Z=\sqrt{{R}^{2}+{X}^{2}}``
`` R=4\,\mathrm{\,\Omega \,}\&X=3\,\mathrm{\,\Omega \,}``
`` \Rightarrow Z=\sqrt{{4}^{2}+{3}^{2}}=5\,\mathrm{\,\Omega \,}``
Page No 329:
- Qstn #8Transformers are used
(a) in DC circuits only
(b) in AC circuits only
(c) in both DC and AC circuits
(d) neither in DC nor in AC circuitsdigAnsr: bAns : (b) in AC circuits only
When a DC supply is provided to a transformer, there will be no change in flux with time across the coils of the transformer. So, there will be no induced emf in the secondary coil due to changing current in the primary coil. Hence, the transformer cannot operate in DC because of the violation of its working principle.
Page No 329:
- Qstn #9An alternating current is given by i = i1 cos ωt + i2 sin ωt. The rms current is given by
(a)
i1+i22
(b)
i1+i22
(c)
i12+i222
(d)
i12+i222digAnsr: cAns : (c) `` \sqrt{\frac{{i}_{1}^{2}+{i}_{2}^{2}}{2}}``
Given:
i = i1 cos ωt + i2 sin ωt
The rms value of current is given by,
`` {i}_{rms}=\sqrt{\frac{{\int }_{0}^{T}{i}^{2}dt}{{\int }_{0}^{T}dt}}``
`` i={i}_{1}\,\mathrm{\,cos\,}\omega t+{i}_{2}\,\mathrm{\,sin\,}\omega t``
`` ``
`` {i}_{\,\mathrm{\,rms\,}}=\sqrt{\frac{{\int }_{0}^{T}{\left({i}_{1}\,\mathrm{\,cos\,}\omega t+{i}_{2}\,\mathrm{\,sin\,}\omega t\right)}^{2}dt}{{\int }_{0}^{T}dt}}``
`` {i}_{\,\mathrm{\,rms\,}}=\sqrt{\frac{{\int }_{0}^{T}\left({i}_{1}^{2}{\,\mathrm{\,cos\,}}^{2}\omega t+{i}_{2}^{2}{\,\mathrm{\,sin\,}}^{2}\omega t+2{i}_{1}{i}_{2}\,\mathrm{\,sin\,}\,\mathrm{\,\omega t\,}\,\mathrm{\,cos\,}\omega t\right)dt}{{\int }_{0}^{T}dt}}``
`` {i}_{\,\mathrm{\,rms\,}}=\sqrt{\frac{{\int }_{0}^{T}\left({i}_{1}^{2}{\displaystyle \frac{(\,\mathrm{\,cos\,}2\omega t+1)}{2}}+{i}_{2}^{2}{\displaystyle \frac{(1-\,\mathrm{\,cos\,}2\omega t)}{2}}+{i}_{1}{i}_{2}\,\mathrm{\,sin\,}2\omega t\right)dt}{{\int }_{0}^{T}dt}}``
`` [\because {\,\mathrm{\,cos\,}}^{2}\omega t=\frac{(\,\mathrm{\,cos\,}2\omega t+1)}{2},{\,\mathrm{\,sin\,}}^{2}\omega t=\frac{(1-\,\mathrm{\,cos\,}2\omega t)}{2}]``
`` ``
`` ``
We know that, T = 2π
Integrating the above expression
`` {i}_{\,\mathrm{\,rms\,}}=\sqrt{\frac{{\displaystyle \frac{1}{2}}{i}_{1}^{2}\left({\int }_{0}^{2\pi }1dt+{\int }_{0}^{2\pi }\,\mathrm{\,cos\,}2\omega tdt\right)+{i}_{2}^{2}\left({\int }_{0}^{2\pi }1dt-{\int }_{0}^{2\pi }\,\mathrm{\,cos\,}2\omega tdt\right)+{i}_{1}{i}_{2}{\int }_{0}^{2\pi }\,\mathrm{\,sin\,}2\omega tdt}{{\int }_{0}^{2\pi }dt}}``
The following integrals become zero
`` {\int }_{0}^{2\pi }\,\mathrm{\,cos\,}2\omega tdt=0={\int }_{0}^{2\pi }\,\mathrm{\,sin\,}2\omega tdt``
`` ``
Therefore, it becomes
`` {i}_{\,\mathrm{\,rms\,}}=\sqrt{\frac{{\displaystyle \frac{{i}_{1}^{2}}{2}}\left({\int }_{0}^{2\,\mathrm{\,\pi \,}}1dt\right)+{\displaystyle \frac{{i}_{2}^{2}}{2}}\left({\int }_{0}^{2\,\mathrm{\,\pi \,}}1dt\right)}{{\int }_{0}^{2\pi }dt}}``
`` {i}_{\,\mathrm{\,rms\,}}=\sqrt{\frac{{\displaystyle \frac{{i}_{1}^{2}}{2}}\times 2\,\mathrm{\,\pi \,}+{\displaystyle \frac{{i}_{2}^{2}}{2}}\times 2\,\mathrm{\,\pi \,}}{2\,\mathrm{\,\pi \,}}}``
`` \Rightarrow {i}_{\,\mathrm{\,rms\,}}=\sqrt{\frac{{i}_{1}^{2}+{i}_{2}^{2}}{2}}``
Page No 329:
- Qstn #10An alternating current of peak value 14 A is used to heat a metal wire. To produce the same heating effect, a constant current i can be used, where i is
(a) 14 A
(b) about 20 A
(c) 7 A
(d) about 10 AdigAnsr: dAns : (d) about 10 A
The rms value of an alternating current is equivalent to the constant current. So, the heating effect produced is actually measured in terms of the rms value, in case of alternating current. The constant current is, thus, equal to the rms value of alternating current, which is given by,
`` {I}_{rms}=\frac{{I}_{peak}}{\sqrt{2}}=\frac{14}{\sqrt{2}}=9.9\approx 10\,\mathrm{\,A\,}``
Page No 329:
- Qstn #11A constant current of 2.8 A exists in a resistor. The rms current is
(a) 2.8 A
(b) about 2 A
(c) 1.4 A
(d) undefined for a direct currentdigAnsr: aAns : (a) 2.8 A
The constant current is equal to the rms value of current. So,
Irms = 2.8 A
Page No 329:
- #Section : iii
- Qstn #1An inductor, a resistance and a capacitor are joined in series with an AC source. As the frequency of the source is slightly increased from a very low value, the reactance
(a) of the inductor increases
(b) of the resistor increases
(c) of the capacitor increases
(d) of the circuit increasesdigAnsr: aAns : (a) of the inductor increases
The reactance of an inductor is given by,
`` {X}_{L}=\omega L``
And the reactance of a capacitor is given by,
`` {X}_{C}=\frac{1}{\omega C}``
Here, ω = 2πf , where f is the frequency of the source. So, when f increases, ω increases.
∴ XL will increase and XC will decrease.
Page No 329: