NEET-XII-Physics
39: Alternating Current
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #2The reactance of a circuit is zero. It is possible that the circuit contains
(a) an inductor and a capacitor
(b) an inductor but no capacitor
(c) a capacitor but no inductor
(d) neither an inductor nor a capacitordigAnsr: a,d,b,cAns : (a) an inductor and a capacitor
(d) neither an inductor nor a capacitor
(a) The reactance of a circuit containing a capacitor and an inductor is given by,
`` X={X}_{L}-{X}_{C}=\omega L-\frac{1}{\omega C}``
`` ``
If `` \omega L=\frac{1}{\omega C}``, X = 0. So, the circuit contains an inductor and a capacitor.
(b) For a circuit without a capacitor, reactance is given by,
`` {X}^{\text{'}}={X}_{L}=\omega L``, which cannot be zero for an AC source.
(c) Similarly, for a circuit without an inductor, reactance is given by,
`` {X}^{\text{'}\text{'}}={X}_{C}=\frac{1}{\omega C}``, which also cannot be zero.
(d) For a circuit without any capacitor and inductor, reactance, X' = 0 ( L = C = 0)
Page No 330:
- Qstn #3In an AC series circuit, the instantaneous current is zero when the instantaneous voltage is maximum. Connected to the source may be a
(a) pure inductor
(b) pure capacitor
(c) pure resistor
(d) combination of an inductor and a capacitordigAnsr: a,b,dAns : (a) pure inductor
(b) pure capacitor
(d) combination of an inductor and a capacitor.
For a pure inductive circuit, voltage leads the current by `` 90°``. So, the instantaneous current is zero when the instantaneous voltage is maximum.
Similar is the case with a purely capacitive circuit, in which, current leads the voltage by `` 90°``.
Also, in a circuit containing a combination of inductor and capacitor, the current may lead or lag the voltage by `` 90°``, depending upon whether the voltage across the inductor or the capacitor is greater. Here too, there is a phase difference of `` 90°`` between the voltage and current. Hence, the the instantaneous current is zero when the instantaneous voltage is maximum.
Page No 330:
- Qstn #4An inductor coil of some resistance is connected to an AC source. Which of the following quantities have zero average value over a cycle?
(a) Current
(b) Induced emf in the inductor
(c) Joule heat
(d) Magnetic energy stored in the inductordigAnsr: a,bAns : (a) Current
(b) Induced emf in the inductor
For a series L-R circuit, the AC current can be given by,
`` i={i}_{0}\,\mathrm{\,sin\,}\omega t``
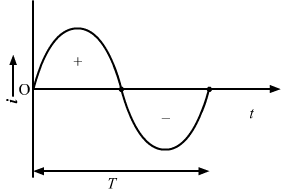
From the graph, we can see that the average value of current over a cycle is zero.
Since it a series L-R circuit, the phase difference between current and voltage is `` \frac{\pi }{2}``. The AC voltage can be given by,
`` V={V}_{0}\,\mathrm{\,cos\,}\omega t``
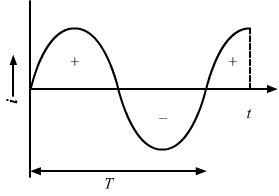
From the graph, we can see that the average value of voltage over a cycle is also zero.
Joule's heat through the resistor is given by,
`` {H}_{avg}={{i}_{rms}}^{2}R``, which is non zero.
Similarly, magnetic energy stored in the inductor is given by,
`` {U}_{avg}=\frac{1}{2}L{{i}_{rms}}^{2}`` , which is also non-zero.
Page No 330:
- Qstn #5The AC voltage across a resistance can be measured using
(a) a potentiometer
(b) a hot-wire voltmeter
(c) a moving-coil galvanometer
(d) a moving-magnet galvanometerdigAnsr: bAns : (b) a hot-wire voltmeter
Only a hot-wire voltmeter can be used to measure an AC voltage across a resistor.
Page No 330:
- Qstn #6To convert mechanical energy into electrical energy, one can use
(a) DC dynamo
(b) AC dynamo
(c) motor
(d) transformerdigAnsr: a,bAns : (a) DC dynamo
(b) AC dynamo
An AC or DC dynamo can be used to convert mechanical energy to electrical energy.
A motor converts electrical energy to mechanical energy and a transformer is used to step up or down the voltage or simply to transfer electrical energy.
Page No 330:
- Qstn #7An AC source rated 100 V (rms) supplies a current of 10 A (rms) to a circuit. The average power delivered by the source
(a) must be 1000 W
(b) may be 1000 W
(c) may be greater than 1000 W
(d) may be less than 1000 WdigAnsr: b,dAns : (b) may be 1000 W
(d) may be less than 1000 W
The average power delivered by an AC source is given by,
`` {P}_{avg}={V}_{rms}{I}_{rms}\,\mathrm{\,cos\,}\varphi ``
Given:
Vrms = 100 V
Irms = 10 A
`` \Rightarrow {P}_{avg}=1000\,\mathrm{\,cos\,}\varphi ``
`` \because \varphi \in \left(-\frac{\,\mathrm{\,\pi \,}}{2},\frac{\,\mathrm{\,\pi \,}}{2}\right)``
`` \Rightarrow \,\mathrm{\,cos\,}\varphi \in \left(0,1\right)``
`` \therefore 0\le {P}_{avg}\le 1000``
Page No 330:
- #Section : iv
- Qstn #1Find the time required for a 50 Hz alternating current to change its value from zero to the rms value.Ans : Frequency of alternating current, f = 50 Hz
Alternation current `` \left(i\right)`` is given by,
i = i0sinωt ...(1)
Here, i0 = peak value of current
Root mean square value of current `` \left({i}_{rms}\right)`` is given by,
`` {i}_{\,\mathrm{\,rms\,}}=\frac{{i}_{0}}{\sqrt{2}}...\left(1\right)``
`` ``
On substituting the value of the root mean square value of current in place of alternating current in equation (1), we get:
`` \frac{{i}_{0}}{\sqrt{2}}={i}_{0}\,\mathrm{\,sin\,}\omega t``
`` \Rightarrow \frac{1}{\sqrt{2}}=\,\mathrm{\,sin\,}\omega t=\,\mathrm{\,sin\,}\frac{\,\mathrm{\,\pi \,}}{4}``
`` \Rightarrow \frac{\,\mathrm{\,\pi \,}}{4}=\,\mathrm{\,\omega \,}t``
`` \Rightarrow t\mathit{=}\frac{\,\mathrm{\,\pi \,}}{4\omega }=\frac{\,\mathrm{\,\pi \,}}{4\times 2\,\mathrm{\,\pi \,}f}\left(\because \omega =2\,\mathrm{\,\pi \,}f\right)``
`` =\frac{1}{8f}=\frac{1}{8\times 50}``
`` =\frac{1}{400}=0.0025\,\mathrm{\,s\,}``
`` =2.5\,\mathrm{\,ms\,}``
Page No 330:
- Qstn #2The household supply of electricity is at 220 V (rms value) and 50 Hz. Find the peak voltage and the least possible time in which the voltage can change from the rms value to zero.Ans : RMS value of voltage, Erms = 220 V,
Frequency of alternating current, f = 50 Hz
(a) Peak value of voltage `` \left({E}_{0}\right)`` is given by,
`` {E}_{0}={E}_{\,\mathrm{\,rms\,}}\sqrt{2}``
`` ``,
where Erms = root mean square value of voltage
`` {E}_{0}={E}_{\,\mathrm{\,rms\,}}\sqrt{2}``
`` \Rightarrow {E}_{0}=\sqrt{2}\times 220``
`` \Rightarrow {E}_{0}=311.08\,\mathrm{\,V\,}=311\,\mathrm{\,V\,}``
(b) Voltage `` \left(E\right)`` is given by,
`` E={E}_{0}\,\mathrm{\,sin\,}\omega t``,
where E0 = peak value of voltage
Time taken for the current to reach zero from the rms value = Time taken for the current to reach the rms value from zero
In one complete cycle, current starts from zero and again reaches zero.
So, first we need to find the time taken for the current to reach the rms value from zero.
`` \,\mathrm{\,As\,}E=\frac{{E}_{0}}{\sqrt{2}},``
`` \frac{{E}_{0}}{\sqrt{2}}={E}_{0}\,\mathrm{\,sin\,}\omega t``
`` \Rightarrow \omega t=\frac{\,\mathrm{\,\pi \,}}{4}``
`` \Rightarrow t=\frac{\,\mathrm{\,\pi \,}}{4\omega }=\frac{\,\mathrm{\,\pi \,}}{4\times 2\,\mathrm{\,\pi \,}f}``
`` \Rightarrow t=\frac{\,\mathrm{\,\pi \,}}{8\,\mathrm{\,\pi \,}50}=\frac{1}{400}``
`` \Rightarrow t=2.5\,\mathrm{\,ms\,}``
`` ``
Thus, the least possible time in which voltage can change from the rms value to zero is 2.5 ms.
Page No 330:
- Qstn #3A bulb rated 60 W at 220 V is connected across a household supply of alternating voltage of 220 V. Calculate the maximum instantaneous current through the filament.Ans : Power of the bulb, P = 60 W
Voltage at the bulb, V = 220 V
RMS value of alternating voltage, Erms = 220 V
P = V2R,
where R = resistance of the bulb
`` \therefore R\mathit{=}\frac{{V}^{\mathit{2}}}{P}=\frac{220\times 220}{60}``
`` =806.67``
`` ``
Peak value of voltage `` \left({E}_{0}\right)`` is given by,
`` {E}_{0}={E}_{\,\mathrm{\,rms\,}}\sqrt{2}``
=`` 220\times \sqrt{2}``
= 311.08
Now, maximum current through the filament `` \left({i}_{0}\right)`` is,
`` {i}_{0}=\frac{{E}_{0}}{R}``
`` \Rightarrow {i}_{0}=\frac{311.08}{806.67}=0.39\,\mathrm{\,A\,}``
Page No 330:
- Qstn #4An electric bulb is designed to operate at 12 volts DC. If this bulb is connected to an AC source and gives normal brightness, what would be the peak voltage of the source?Ans : Voltage across the electric bulb, E = 12 volts
Let E0 be the peak value of voltage.
We know that heat produced by passing an alternating current`` \left(i\right)`` through a resistor is equal to heat produced by passing a constant current`` \left({i}_{rms}\right)`` through the same resistor. If R is the resistance of the electric bulb and T is the temperature, then
`` {i}^{\mathit{2}}RT\mathit{=}{i}_{\mathit{rms}}^{\mathit{2}}RT``
`` \Rightarrow \frac{{E}^{\mathit{2}}}{{R}^{\mathit{2}}}\mathit{=}\frac{{E}_{\mathit{rms}}^{\mathit{2}}}{{R}^{\mathit{2}}}``
`` \Rightarrow {E}^{\mathit{2}}\mathit{=}\frac{{E}_{\mathit{0}}^{\mathit{2}}}{\mathit{2}}\left(\mathit{\because }{{E}^{\mathit{2}}}_{rms}\mathit{=}\frac{{{E}^{\mathit{2}}}_{\mathit{0}}}{\mathit{2}}\right)``
`` \Rightarrow {E}_{0}^{2}=2{E}^{2}``
`` \Rightarrow {E}_{0}^{2}=2\times {\left(12\right)}^{2}=2\times 144``
`` \Rightarrow {E}_{0}=\sqrt{2\times 144}``
`` =16.97=17\,\mathrm{\,V\,}``
Thus , peak value of voltage is 17 V.
Page No 330:
- Qstn #5The peak power consumed by a resistive coil, when connected to an AC source, is 80 W. Find the energy consumed by the coil in 100 seconds, which is many times larger than the time period of the source.Ans : Peak power of the resistive coil, `` {P}_{0}=80\,\mathrm{\,W\,}``
Time, t = 100 s
RMS value of power `` \left({P}_{rms}\right)`` is given by,
`` {P}_{\,\mathrm{\,rms\,}}=\frac{{P}_{0}}{2}``,
where P0 = Peak value of power
`` \therefore {P}_{\,\mathrm{\,rms\,}}=\frac{{P}_{0}}{2}=40\,\mathrm{\,W\,}``
Energy consumed `` \left(E\right)`` is given by,
E = Prms × t
= 40 × 100
= 4000 J = 4.0 kJ
Page No 330:
- Qstn #6The dielectric strength of air is 3.0 × 106 V/m. A parallel-plate air-capacitor has area 20 cm2 and plate separation 0.10 mm. Find the maximum rms voltage of an AC source that can be safely connected to this capacitor.Ans : Given:
Area of parallel-plate air-capacitor, A = 20 cm2
Separation between the plates, d = 0.1 mm
Dielectric strength of air, E= 3 × 106 V/m
E = `` \frac{V}{d}``,
where V = potential difference across the capacitor
`` \therefore `` V = Ed
= 3 × 106 × 0.1 × 10-3
= 3 × 102 = 300 V
Thus, peak value of voltage is 300 V.
Maximum rms value of voltage `` \left({V}_{\,\mathrm{\,rms\,}}\right)`` is given by,
`` {V}_{\,\mathrm{\,rms\,}}=\frac{{V}_{0}}{\sqrt{2}}``
`` =\frac{300}{\sqrt{2}}=212\,\mathrm{\,V\,}``
Page No 330:
- Qstn #7The current in a discharging LR circuit is given by i = i0 e-t/τ , where τ is the time constant of the circuit. Calculate the rms current for the period t = 0 to t = τ.Ans : As per the question,
`` i={i}_{0}{e}^{\frac{-t}{\tau }}``
We need to find the rms current. So, taking the average of i within the limits 0 to τ and then dividing by the given time period τ, we get:
`` {{i}_{\,\mathrm{\,rms\,}}}^{2}=\frac{1}{\tau }{\int }_{\mathit{0}}^{\tau }{i}_{0}^{2}{\,\mathrm{\,e\,}}^{\mathit{-}\mathit{2}t\mathit{/}\tau }dt``
`` \Rightarrow {{i}_{rms}}^{2}=\frac{{i}_{0}^{2}}{\tau }{\int }_{0}^{\,\mathrm{\,\tau \,}}{\,\mathrm{\,e\,}}^{\mathit{-}\mathit{2}t\mathit{/}\tau }dt``
`` =\frac{{i}_{0}^{2}}{\tau }\times {\left[\frac{-\tau }{2}{\,\mathrm{\,e\,}}^{\mathit{-}\mathit{2}t\mathit{/}\tau }\right]}_{0}^{\tau }``
`` =-\frac{{i}_{0}^{2}}{\tau }\times \frac{\tau }{2}\times \left[{\,\mathrm{\,e\,}}^{-2}-1\right]``
`` =\frac{{{i}_{0}}^{2}}{2}(1-\frac{1}{{\,\mathrm{\,e\,}}^{2}})``
`` {i}_{\,\mathrm{\,rms\,}}=\frac{{i}_{0}}{e}\sqrt{\frac{{e}^{2}-1}{2}}``
Page No 330:
- Qstn #8A capacitor of capacitance 10 μF is connected to an oscillator with output voltage ε = (10 V) sin ωt. Find the peak currents in the circuit for ω = 10 s-1, 100 s-1, 500 s-1 and 1000 s-1.Ans : Capacitance of the capacitor, C = 10 μF = 10 × 10-6 F = 10-5 F
Output voltage of the oscillator, `` \epsilon ``= (10 V)sinωt
On comparing the output voltage of the oscillator with `` \epsilon ={\epsilon }_{0}\,\mathrm{\,sin\,}\omega t``, we get:
Peak voltage `` {\epsilon }_{0}`` = 10 V
For a capacitive circuit,
Reactance, `` {X}_{c}=\frac{1}{\omega C}``
Here, `` \omega `` = angular frequency
C = capacitor of capacitance
Peak current, `` {I}_{0}`` = `` \frac{{\epsilon }_{0}}{{X}_{c}}``
(a) At ω = 10 s-1:
Peak current,
I0 = `` \frac{{\epsilon }_{0}}{{X}_{c}}``
`` =\frac{{\epsilon }_{0}}{1\mathit{/}\omega C}``
`` =\frac{10}{1/10\times {10}^{-5}}\,\mathrm{\,A\,}``
= 1 × 10-3 A
(b) At ω = 100 s-1:
Peak current, I0 = `` \frac{{\epsilon }_{0}}{1/\omega C}``
`` \Rightarrow {I}_{0}=\frac{10}{1/100\times {10}^{-5}}``
`` \Rightarrow {I}_{0}=\frac{10}{{10}^{3}}=1\times {10}^{-2}\,\mathrm{\,A\,}``
`` =0.01\,\mathrm{\,A\,}``
(c) At ω = 500 s-1:
Peak current, I0 = `` \frac{{\epsilon }_{0}}{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\omega C$}\right.}}``
`` {I}_{0}=\frac{{\epsilon }_{0}}{1/\omega C}``
`` \Rightarrow {I}_{0}=\frac{10}{1/500\times {10}^{-5}}``
`` \Rightarrow {I}_{0}=10\times 500\times {10}^{-5}``
`` =5\times {10}^{-2}\,\mathrm{\,A\,}=0.05\,\mathrm{\,A\,}``
(d) At ω = 1000 s-1:
Peak current, I0 = `` \frac{{\epsilon }_{0}}{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\omega C$}\right.}}``
`` \Rightarrow {I}_{0}=\frac{10}{1/1000\times {10}^{-5}}``
`` \Rightarrow {I}_{0}=10\times 1000\times {10}^{-5}``
`` \Rightarrow {I}_{0}={10}^{-1}\,\mathrm{\,A\,}=0.1\,\mathrm{\,A\,}``
Page No 330: