NEET-XII-Physics
39: Alternating Current
- #4An AC source is rated 220 V, 50 Hz. The average voltage is calculated in a time interval of 0.01 s. It
(a) must be zero
(b) may be zero
(c) is never zero
(d)
is 220/2 VdigAnsr: bAns : (b) may be zero
Let the AC voltage be given by,
`` V={V}_{0}\,\mathrm{\,sin\,}\omega t``
Here, ω = 2`` \pi ``f = 314 rad/s
The average voltage over the given time,
`` {V}_{avg}=\frac{{\int }_{0}^{0.01}Vdt}{{\int }_{0}^{0.01}dt}=-{V}_{0}{\left[\frac{\,\mathrm{\,cos\,}\omega t}{\omega }\right]}_{0}^{0.01}``
`` =\frac{{V}_{0}}{\omega \times 0.01}\left(1-\,\mathrm{\,cos\,}\omega \left(0.01\right)\right)``
`` =\frac{{V}_{0}}{314\times 0.01}\left(1-\,\mathrm{\,cos\,}\left(314\times 0.01\right)\right)``
`` =\frac{{V}_{0}}{3.14}\left(1-\,\mathrm{\,cos\pi \,}\right)``
`` =\frac{2{V}_{0}}{\,\mathrm{\,\pi \,}}=140.127\,\mathrm{\,V\,}``
Also, when `` V={V}_{0}\,\mathrm{\,cos\,}\omega t``,
`` {V}_{avg}=\frac{{\int }_{0}^{0.01}Vdt}{{\int }_{0}^{0.01}dt}={V}_{0}{\left[\frac{\,\mathrm{\,sin\,}\omega t}{\omega }\right]}_{0}^{0.01}``
`` =\frac{{V}_{0}}{\omega \times 0.01}\left(\,\mathrm{\,sin\,}\omega \left(0.01\right)-0\right)``
`` =\frac{{V}_{0}}{314\times 0.01}\left(\,\mathrm{\,sin\,}\left(314\times 0.01\right)\right)``
`` =\frac{{V}_{0}}{3.14}\left(\,\mathrm{\,sin\,}\pi \right)``
`` =0``
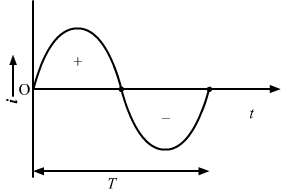
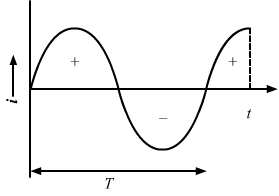
From the above results, we can say that the average voltage can be zero. But it is not necessary that it should be zero or never zero.
Page No 329: