12: Atoms : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

12: Atoms

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#
4 - Atoms

Qstn #1
Choose the correct alternative from the clues given at the end of the each statement:

#1-a
The size of the atom in Thomson’s model is .......... the atomic size in Rutherford’s model. (much greater than/no different from/much less than.)
Ans : The sizes of the atoms taken in Thomson’s model and Rutherford’s model have the same order of magnitude.

#1-b
In the ground state of .......... electrons are in stable equilibrium, while in .......... electrons always experience a net force.

(Thomson’s model/ Rutherford’s model.)

Ans : In the ground state of Thomson’s model, the electrons are in stable equilibrium. However, in Rutherford’s model, the electrons always experience a net force.

#1-c
A classical atom based on .......... is doomed to collapse.

(Thomson’s model/ Rutherford’s model.)

Ans : A classical atom based on Rutherford’s model is doomed to collapse.

#1-d
An atom has a nearly continuous mass distribution in a .......... but has a highly non-uniform mass distribution in ..........

(Thomson’s model/ Rutherford’s model.)

Ans : An atom has a nearly continuous mass distribution in Thomson’s model, but has a highly non-uniform mass distribution in Rutherford’s model.

#1-e
The positively charged part of the atom possesses most of the mass in .......... (Rutherford’s model/both the models.)
Ans : The positively charged part of the atom possesses most of the mass in both the models.

Qstn #2
Suppose you are given a chance to repeat the alpha-particle scattering experiment using a thin sheet of solid hydrogen in place of the gold foil. (Hydrogen is a solid at temperatures below 14 K.) What results do you expect?

Ans : In the alpha-particle scattering experiment, if a thin sheet of solid hydrogen is used in place of a gold foil, then the scattering angle would not be large enough. This is because the mass of hydrogen (1.67 × 10^-27kg) is less than the mass of incident α-particles (6.64 × 10^-27kg). Thus, the mass of the scattering particle is more than the target nucleus (hydrogen). As a result, the α-particles would not bounce back if solid hydrogen is used in the α-particle scattering experiment.

Qstn #3
What is the shortest wavelength present in the Paschen series of spectral lines?

Ans : Rydberg’s formula is given as:

Where,

h = Planck’s constant = 6.6 × 10^-34 Js

c = Speed of light = 3 × 10⁸m/s

(n₁ and n₂ are integers)

The shortest wavelength present in the Paschen series of the spectral lines is given for values n₁ = 3 and n₂ = ∞.

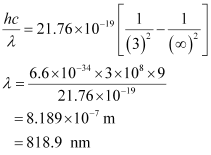
Qstn #4
A difference of 2.3 eV separates two energy levels in an atom. What is the frequency of radiation emitted when the atom makes a transition from the upper level to the lower level?

Ans : Separation of two energy levels in an atom,

E = 2.3 eV

= 2.3 × 1.6 × 10^-19

= 3.68 × 10^-19 J

Let ν be the frequency of radiation emitted when the atom transits from the upper level to the lower level.

We have the relation for energy as:

E = hv

Where,

h = Planck’s constant

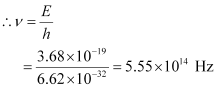
Hence, the frequency of the radiation is 5.6 × 10¹⁴ Hz.

Qstn #5
The ground state energy of hydrogen atom is -13.6 eV. What are the kinetic and potential energies of the electron in this state?

Ans : Ground state energy of hydrogen atom, E = - 13.6 eV

This is the total energy of a hydrogen atom. Kinetic energy is equal to the negative of the total energy.

Kinetic energy = - E = - (- 13.6) = 13.6 eV

Potential energy is equal to the negative of two times of kinetic energy.

Potential energy = - 2 × (13.6) = - 27 .2 eV

Qstn #6
A hydrogen atom initially in the ground level absorbs a photon, which excites it to the n = 4 level. Determine the wavelength and frequency of the photon.

Ans : For ground level, n₁ = 1

Let E₁ be the energy of this level. It is known that E₁ is related with n₁ as:

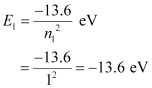
The atom is excited to a higher level, n₂ = 4.

Let E₂ be the energy of this level.

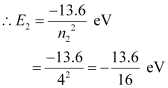
The amount of energy absorbed by the photon is given as:

E = E₂ - E₁

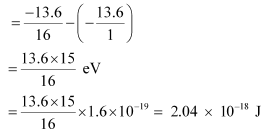
For a photon of wavelengthλ, the expression of energy is written as:

Where,

h = Planck’s constant = 6.6 × 10^-34 Js

c = Speed of light = 3 × 10⁸ m/s

And, frequency of a photon is given by the relation,

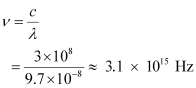
Hence, the wavelength of the photon is 97 nm while the frequency is 3.1 × 10¹⁵ Hz.

#7

#7-a
Using the Bohr’s model calculate the speed of the electron in a hydrogen atom in the n = 1, 2, and 3 levels.
Ans : Let ν₁ be the orbital speed of the electron in a hydrogen atom in the ground state level, n₁ = 1. For charge (e) of an electron, ν₁is given by the relation,

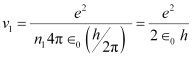
Where,

e = 1.6 × 10^-19 C

∈₀ = Permittivity of free space = 8.85 × 10^-12 N^-1 C² m^-2

h = Planck’s constant = 6.62 × 10^-34 Js

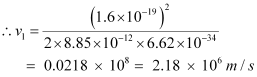
For level n₂ = 2, we can write the relation for the corresponding orbital speed as:

And, for n₃ = 3, we can write the relation for the corresponding orbital speed as:

Hence, the speed of the electron in a hydrogen atom in n = 1, n=2, and n=3 is 2.18 × 10⁶ m/s, 1.09 × 10⁶ m/s, 7.27 × 10⁵ m/s respectively.

#7-b
Calculate the orbital period in each of these levels.
Ans : Let T₁ be the orbital period of the electron when it is in level n₁ = 1.

Orbital period is related to orbital speed as:

Where,

r₁ = Radius of the orbit

h = Planck’s constant = 6.62 × 10^-34 Js

e = Charge on an electron = 1.6 × 10^-19 C

∈₀= Permittivity of free space = 8.85 × 10^-12 N^-1 C² m^-2

m = Mass of an electron = 9.1 × 10^-31 kg

For level n₂ = 2, we can write the period as:

Where,

r₂ = Radius of the electron in n₂ = 2

And, for level n₃ = 3, we can write the period as:

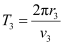
Where,

r₃ = Radius of the electron in n₃ = 3

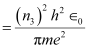
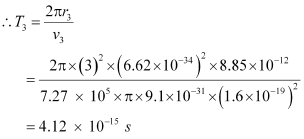
Hence, the orbital period in each of these levels is 1.52 × 10^-16 s, 1.22 × 10^-15 s, and 4.12 × 10^-15 s respectively.