HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

12: Atoms

 page 2

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #8
    The radius of the innermost electron orbit of a hydrogen atom is 5.3 ×10-11 m. What are the radii of the n = 2 and n =3 orbits?
    Ans : The radius of the innermost orbit of a hydrogen atom, r1 = 5.3 × 10-11 m.

    Let r2 be the radius of the orbit at n = 2. It is related to the radius of the innermost orbit as:



    For n = 3, we can write the corresponding electron radius as:



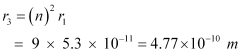
    Hence, the radii of an electron for n = 2 and n = 3 orbits are 2.12 × 10-10 m and 4.77 × 10-10 m respectively.
  • Qstn #9
    A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. What series of wavelengths will be emitted?
    Ans : It is given that the energy of the electron beam used to bombard gaseous hydrogen at room temperature is 12.5 eV. Also, the energy of the gaseous hydrogen in its ground state at room temperature is -13.6 eV.

    When gaseous hydrogen is bombarded with an electron beam, the energy of the gaseous hydrogen becomes -13.6 + 12.5 eV i.e., -1.1 eV.

    Orbital energy is related to orbit level (n) as:



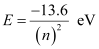
    For n = 3,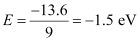

    This energy is approximately equal to the energy of gaseous hydrogen. It can be concluded that the electron has jumped from n = 1 to n = 3 level.

    During its de-excitation, the electrons can jump from n = 3 to n = 1 directly, which forms a line of the Lyman series of the hydrogen spectrum.

    We have the relation for wave number for Lyman series as:



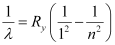
    Where,

    Ry = Rydberg constant = 1.097 × 107 m-1

    λ= Wavelength of radiation emitted by the transition of the electron

    For n = 3, we can obtain λas:



    If the electron jumps from n = 2 to n = 1, then the wavelength of the radiation is given as:



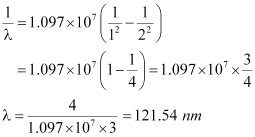
    If the transition takes place from n = 3 to n = 2, then the wavelength of the radiation is given as:



    This radiation corresponds to the Balmer series of the hydrogen spectrum.

    Hence, in Lyman series, two wavelengths i.e., 102.5 nm and 121.5 nm are emitted. And in the Balmer series, one wavelength i.e., 656.33 nm is emitted.
  • Qstn #10
    In accordance with the Bohr’s model, find the quantum number that characterises the earth’s revolution around the sun in an orbit of radius 1.5 × 1011 m with orbital speed 3 × 104 m/s. (Mass of earth = 6.0 × 1024 kg.)
    Ans : Radius of the orbit of the Earth around the Sun, r = 1.5 × 1011 m

    Orbital speed of the Earth, ν = 3 × 104 m/s

    Mass of the Earth, m = 6.0 × 1024 kg

    According to Bohr’s model, angular momentum is quantized and given as:



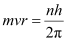
    Where,

    h = Planck’s constant = 6.62 × 10-34 Js

    n = Quantum number



    Hence, the quanta number that characterizes the Earth’ revolution is 2.6 × 1074.
  • Qstn #11
    Answer the following questions, which help you understand the difference between Thomson’s model and Rutherford’s model better.
  • #11-a
    Is the average angle of deflection of α­-particles by a thin gold foil predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
    Ans : about the same

    The average angle of deflection of α­-particles by a thin gold foil predicted by Thomson’s model is about the same size as predicted by Rutherford’s model. This is because the average angle was taken in both models.
  • #11-b
    Is the probability of backward scattering (i.e., scattering of α-particles at angles greater than 90°) predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?
    Ans : much less

    The probability of scattering of α-particles at angles greater than 90° predicted by Thomson’s model is much less than that predicted by Rutherford’s model.
  • #11-c
    Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α-particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide?
    Ans : Scattering is mainly due to single collisions. The chances of a single collision increases linearly with the number of target atoms. Since the number of target atoms increase with an increase in thickness, the collision probability depends linearly on the thickness of the target.
  • #11-d
    In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of α-particles by a thin foil?
    Ans : Thomson’s model

    It is wrong to ignore multiple scattering in Thomson’s model for the calculation of average angle of scattering of α­-particles by a thin foil. This is because a single collision causes very little deflection in this model. Hence, the observed average scattering angle can be explained only by considering multiple scattering.
  • Qstn #12
    The gravitational attraction between electron and proton in a hydrogen atom is weaker than the coulomb attraction by a factor of about 10-40. An alternative way of looking at this fact is to estimate the radius of the first Bohr orbit of a hydrogen atom if the electron and proton were bound by gravitational attraction. You will find the answer interesting.
    Ans : Radius of the first Bohr orbit is given by the relation,



    Where,

    ∈0 = Permittivity of free space

    h = Planck’s constant = 6.63 × 10-34 Js

    me = Mass of an electron = 9.1 × 10-31 kg

    e = Charge of an electron = 1.9 × 10-19 C

    mp = Mass of a proton = 1.67 × 10-27 kg

    r = Distance between the electron and the proton

    Coulomb attraction between an electron and a proton is given as:

    Gravitational force of attraction between an electron and a proton is given as:



    Where,

    G = Gravitational constant = 6.67 × 10-11 N m2/kg2

    If the electrostatic (Coulomb) force and the gravitational force between an electron and a proton are equal, then we can write:

    ∴FG = FC



    Putting the value of equation (4) in equation (1), we get:



    It is known that the universe is 156 billion light years wide or 1.5 × 1027 m wide. Hence, we can conclude that the radius of the first Bohr orbit is much greater than the estimated size of the whole universe.
  • Qstn #13
    Obtain an expression for the frequency of radiation emitted when a hydrogen atom de-excites from level n to level (n-1). For large n, show that this frequency equals the classical frequency of revolution of the electron in the orbit.
    Ans : It is given that a hydrogen atom de-excites from an upper level (n) to a lower level (n-1).

    We have the relation for energy (E1) of radiation at level n as:



    Now, the relation for energy (E2) of radiation at level (n - 1) is givenas: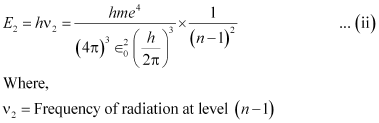

    Energy (E) released as a result of de-excitation:

    E = E2-E1

    hν = E2 - E1 ... (iii)

    Where,

    ν = Frequency of radiation emitted

    Putting values from equations (i) and (ii) in equation (iii), we get:



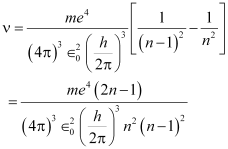
    For large n, we can write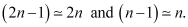



    Classical relation of frequency of revolution of an electron is given as:

    Where,

    Velocity of the electron in the nth orbit is given as:

    v =

    And, radius of the nth orbit is given as:

    r =

    Putting the values of equations (vi) and (vii) in equation (v), we get:



    Hence, the frequency of radiation emitted by the hydrogen atom is equal to its classical orbital frequency.
  • Qstn #14
    Classically, an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size? Why is an atom not, say, thousand times bigger than its typical size? The question had greatly puzzled Bohr before he arrived at his famous model of the atom that you have learnt in the text. To simulate what he might well have done before his discovery, let us play as follows with the basic constants of nature and see if we can get a quantity with the dimensions of length that is roughly equal to the known size of an atom (~ 10-10 m).
  • #14-a
    Construct a quantity with the dimensions of length from the fundamental constants e, me, and c. Determine its numerical value.
    (b) You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non-relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for ‘something else’ to get the right atomic size. Now, the Planck’s constant h had already made its appearance elsewhere. Bohr’s great insight lay in recognising that h, me, and e will yield the right atomic size. Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.
    Ans : Charge on an electron, e = 1.6 × 10-19 C

    Mass of an electron, me = 9.1 × 10-31 kg

    Speed of light, c = 3 ×108 m/s

    Let us take a quantity involving the given quantities as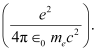

    Where,

    ∈0 = Permittivity of free space

    And,

    The numerical value of the taken quantity will be:



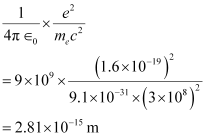
    Hence, the numerical value of the taken quantity is much smaller than the typical size of an atom.
    (b) Charge on an electron, e = 1.6 × 10-19 C

    Mass of an electron, me = 9.1 × 10-31 kg

    Planck’s constant, h = 6.63 ×10-34 Js

    Let us take a quantity involving the given quantities as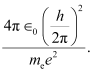

    Where,

    ∈0 = Permittivity of free space

    And,

    The numerical value of the taken quantity will be:



    Hence, the value of the quantity taken is of the order of the atomic size.
  • #14-b
    You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non-relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for ‘something else’ to get the right atomic size. Now, the Planck’s constant h had already made its appearance elsewhere. Bohr’s great insight lay in recognising that h, me, and e will yield the right atomic size. Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.
    Ans : Charge on an electron, e = 1.6 × 10-19 C

    Mass of an electron, me = 9.1 × 10-31 kg

    Planck’s constant, h = 6.63 ×10-34 Js

    Let us take a quantity involving the given quantities as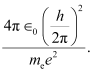

    Where,

    ∈0 = Permittivity of free space

    And,

    The numerical value of the taken quantity will be:



    Hence, the value of the quantity taken is of the order of the atomic size.
  • Qstn #15
    The total energy of an electron in the first excited state of the hydrogen atom is about -3.4 eV.
  • #15-a
    What is the kinetic energy of the electron in this state?
    Ans : Total energy of the electron, E = -3.4 eV

    Kinetic energy of the electron is equal to the negative of the total energy.

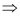    K = -E

    = - (- 3.4) = +3.4 eV

    Hence, the kinetic energy of the electron in the given state is +3.4 eV.
next page