NEET-XII-Physics
01: Electric Charges And Fields
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #25An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 × 104 N C-1 in Millikan’s oil drop experiment. The density of the oil is 1.26 g cm-3. Estimate the radius of the drop. (g = 9.81 m s-2; e = 1.60 × 10-19 C).
Ans : Excess electrons on an oil drop, n = 12
Electric field intensity, E = 2.55 × 104 N C-1
Density of oil, ``\rho`` = 1.26 gm/cm3 = 1.26 × 103 kg/m3
Acceleration due to gravity, g = 9.81 m s-2
Charge on an electron, e = 1.6 × 10-19 C
Radius of the oil drop = r
Force (F) due to electric field E is equal to the weight of the oil drop (W)
F = W
Eq = mg
Ene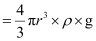
Where,
q = Net charge on the oil drop = ne
m = Mass of the oil drop
= Volume of the oil drop × Density of oil
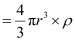
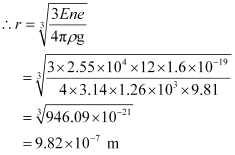
= 9.82 × 10-4 mm
Therefore, the radius of the oil drop is 9.82 × 10-4 mm.
- Qstn #26Which among the curves shown in Fig. 1.35 cannot possibly represent electrostatic field lines?
- #26-a
Ans : The field lines showed in (a) do not represent electrostatic field lines because field lines must be normal to the surface of the conductor.
- #26-b
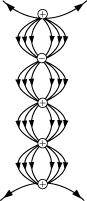
Ans : The field lines showed in (b) do not represent electrostatic field lines because the field lines cannot emerge from a negative charge and cannot terminate at a positive charge.
- #26-c
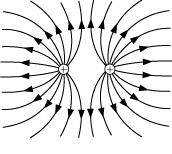
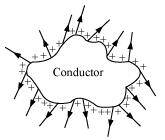
Ans : The field lines showed in (c) represent electrostatic field lines. This is because the field lines emerge from the positive charges and repel each other.
- #26-d
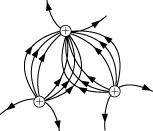
Ans : The field lines showed in (d) do not represent electrostatic field lines because the field lines should not intersect each other.
- #26-e
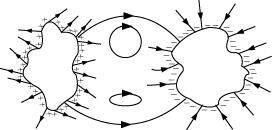
Ans : The field lines showed in (e) do not represent electrostatic field lines because closed loops are not formed in the area between the field lines.
- Qstn #27In a certain region of space, electric field is along the z-direction throughout. The magnitude of electric field is, however, not constant but increases uniformly along the positive z-direction, at the rate of 105 NC-1 per metre. What are the force and torque experienced by a system having a total dipole moment equal to 10-7 Cm in the negative z-direction?
Ans : Dipole moment of the system, p = q × dl = -10-7 C m
Rate of increase of electric field per unit length,
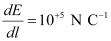
Force (F) experienced by the system is given by the relation,
F = qE
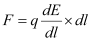
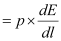
= -10-7 × 10-5
= -10-2 N
The force is -10-2 N in the negative z-direction i.e., opposite to the direction of electric field. Hence, the angle between electric field and dipole moment is 180°.
Torque (Ï„) is given by the relation,
τ = pE sin180°
= 0
Therefore, the torque experienced by the system is zero.
- #28
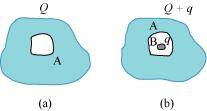
- #28-aA conductor A with a cavity as shown in Fig. 1.36(a) is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor.Ans : Let us consider a Gaussian surface that is lying wholly within a conductor and enclosing the cavity. The electric field intensity E inside the charged conductor is zero.
Let q is the charge inside the conductor and.gif)
is the permittivity of free space.
According to Gauss’s law,
Flux,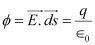
Here, E = 0
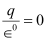
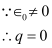
Therefore, charge inside the conductor is zero.
The entire charge Q appears on the outer surface of the conductor.
- #28-bAnother conductor B with charge q is inserted into the cavity keeping B insulated
from A. Show that the total charge on the outside surface of A is Q + q
[Fig. 1.36(b)].Ans : The outer surface of conductor A has a charge of amount Q. Another conductor B having charge +q is kept inside conductor A and it is insulated from A. Hence, a charge of amount -q will be induced in the inner surface of conductor A and +q is induced on the outer surface of conductor A. Therefore, total charge on the outer surface of conductor A is Q + q.
- #28-cA sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way.
Ans : A sensitive instrument can be shielded from the strong electrostatic field in its environment by enclosing it fully inside a metallic surface. A closed metallic body acts as an electrostatic shield.
- Qstn #29A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is
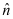, where 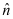is the unit vector in the outward normal direction, and .gif)
is the surface charge density near the hole.
Ans : Let us consider a conductor with a cavity or a hole. Electric field inside the cavity is zero.
Let E is the electric field just outside the conductor, q is the electric charge,is the charge density, and .gif)
is the permittivity of free space.
Charge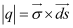
According to Gauss’s law,
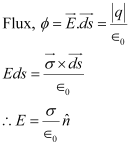
Therefore, the electric field just outside the conductor is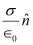
. This field is a superposition of field due to the cavity 
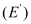and the field due to the rest of the charged conductor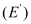. These fields are equal and opposite inside the conductor, and equal in magnitude and direction outside the conductor.
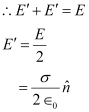
Therefore, the field due to the rest of the conductor is.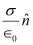
Hence, proved.
- Qstn #30Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Ans : Take a long thin wire XY (as shown in the figure) of uniform linear charge density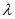
.
Consider a point A at a perpendicular distance l from the mid-point O of the wire, as shown in the following figure.
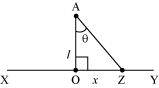
Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ = x
Let q be the charge on this piece.
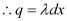
Electric field due to the piece,
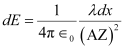
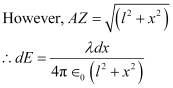
The electric field is resolved into two rectangular components.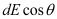
is the perpendicular component and 
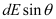is the parallel component.
When the whole wire is considered, the component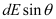 is cancelled.
Only the perpendicular component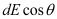 affects point A.
Hence, effective electric field at point A due to the element dx is dE1.
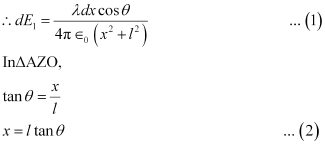
On differentiating equation (2), we obtain
dxdθ=lsec2θdx=lsec2θdθ
From equation (2),
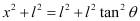
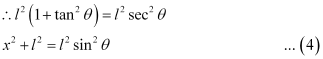
Putting equations (3) and (4) in equation (1), we obtain
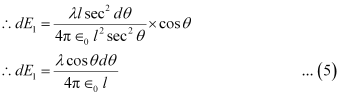
The wire is so long that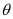
tends from 
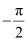to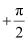 
.
By integrating equation (5), we obtain the value of field E1 as,
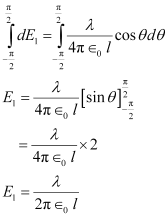
Therefore, the electric field due to long wire is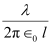
.
- Qstn #31It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up’ quark (denoted by u) of charge (+2/3) e, and the ‘down’ quark (denoted by d) of charge (-1/3) e, together with electrons build up ordinary matter. (Quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.
Ans : A proton has three quarks. Let there be n up quarks in a proton, each having a charge of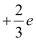
.
Charge due to n up quarks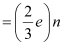
Number of down quarks in a proton = 3 - n
Each down quark has a charge of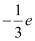
.
Charge due to (3 - n) down quarks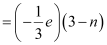
Total charge on a proton = + e
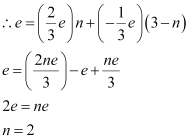
Number of up quarks in a proton, n = 2
Number of down quarks in a proton = 3 - n = 3 - 2 = 1
Therefore, a proton can be represented as ‘uud’.
A neutron also has three quarks. Let there be n up quarks in a neutron, each having a charge of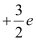
.
Charge on a neutron due to n up quarks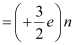
Number of down quarks is 3 - n,each having a charge of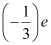
.
Charge on a neutron due to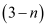
down quarks =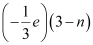 
Total charge on a neutron = 0
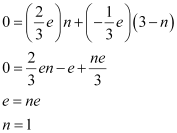
Number of up quarks in a neutron, n = 1
Number of down quarks in a neutron = 3 - n = 2
Therefore, a neutron can be represented as ‘udd’.