NEET-XII-Physics
01: Electric Charges And Fields
- #30Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Ans : Take a long thin wire XY (as shown in the figure) of uniform linear charge density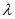
.
Consider a point A at a perpendicular distance l from the mid-point O of the wire, as shown in the following figure.
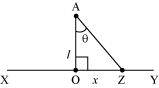
Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ = x
Let q be the charge on this piece.
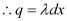
Electric field due to the piece,
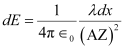
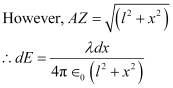
The electric field is resolved into two rectangular components.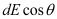
is the perpendicular component and 
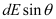is the parallel component.
When the whole wire is considered, the component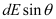 is cancelled.
Only the perpendicular component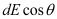 affects point A.
Hence, effective electric field at point A due to the element dx is dE1.
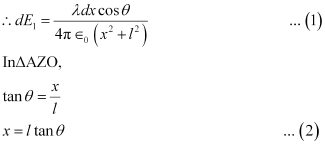
On differentiating equation (2), we obtain
dxdθ=lsec2θdx=lsec2θdθ
From equation (2),
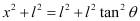
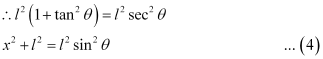
Putting equations (3) and (4) in equation (1), we obtain
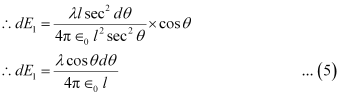
The wire is so long that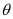
tends from 
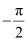to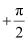 
.
By integrating equation (5), we obtain the value of field E1 as,
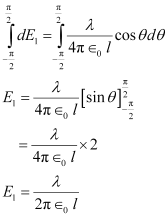
Therefore, the electric field due to long wire is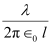
.