05: Newton's Laws Of Motion : Cbse-xi-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

CBSE-XI-Physics

05: Newton's Laws of Motion

with Solutions - page 6

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #18
Suppose the ceiling in the previous problem is that of an elevator which is going up with an acceleration of 2.0 m/s². Find the elongation.
Ans : When the ceiling of the elevator is going up with an acceleration 'a', then a pseudo-force acts on the block in the downward direction.

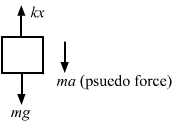
a = 2 m/s²
From the free-body diagram of the block,
kx = mg + ma
⇒ kx = 2g + 2a
= 2 × 9.8 + 2 × 2
= 19.6 + 4
`` \Rightarrow x=\frac{23.6}{100}=0.236\approx 0.24\,\mathrm{\,m \,}``
When 1 kg body is added,
total mass = (2 + 1) kg = 3 kg
Let elongation be x'.
∴ kx' = 3g + 3a = 3 × 9.8 + 6
`` \Rightarrow x\text{ ' }=\frac{35.4}{100}``
`` =0.354\approx 0.36\,\mathrm{\,m \,}``
So, further elongation = x' - x
= 0.36 - 0.24 = 0.12 m.
Page No 80:

Qstn #19
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall to the earth’s surface with a constant velocity v. How much mass should be removed from the balloon so that it may rise with a constant velocity v?
Ans : Let M be mass of the balloon.
Let the air resistance force on balloon be F .
Given that F ∝ v.
⇒ F= kv,
where k = proportionality constant.

When the balloon is moving downward with constant velocity,
B + kv = Mg ...(i)
`` \Rightarrow M=\frac{B+kv}{g}``
Let the mass of the balloon be M' so that it can rise with a constant velocity v in the upward direction.
B = Mg + kv
`` \Rightarrow M\text{ ' }=\frac{B+kv}{g}``
∴ Amount of mass that should be removed = M - M'.
`` ∆M=\frac{B+kv}{g}-\frac{B-kv}{g}``
`` =\frac{B+kv-B+kv}{g}``
`` =\frac{2kv}{g}=\frac{2\left(Mg-B\right)}{g}``
`` =2\left\{M-\frac{B}{g}\right\}``
Page No 80:

Qstn #20
An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
Ans : Let U be the upward force of water acting on the plastic box.
Let m be the initial mass of the plastic box.
When the empty plastic box is accelerating upward,
`` U-mg=\frac{mg}{6}``
`` \Rightarrow U=\frac{7mg}{6}``

`` \Rightarrow m=\frac{6U}{7g}....\left(i\right)``
Let M be the final mass of the box after putting some sand in it.
`` Mg-U=\frac{Mg}{6}``
`` \Rightarrow Mg-\frac{Mg}{6}=U``
`` \Rightarrow M=\frac{6U}{5g}....\left(ii\right)``
Mass added`` =\frac{6U}{5g}-\frac{6U}{7g}``
`` =\frac{6U\left(7-5\right)}{35g}``
`` =\frac{6U·2}{35g}``
From equation (i), `` m=\frac{6U}{7g}``
∴ Mass added`` =\frac{2}{5}m`` .
Page No 80:

Qstn #21
A force
F→=v→×A→is exerted on a particle in addition to the force of gravity, where
v→is the velocity of the particle and
A→is a constant vector in the horizontal direction. With what minimum speed, a particle of mass m be projected so that it continues to move without being defelected and with a constant velocity?
Ans : For the particle to move without being deflected and with constant velocity, the net force on the particle should be zero.
`` \stackrel{\to }{F}+m\stackrel{\to }{g}=0``
`` \Rightarrow \left(\stackrel{\to }{v}\times \stackrel{\to }{A}\right)+\stackrel{\to }{mg}=0``
`` \Rightarrow \left(\stackrel{\to }{v}\times \stackrel{\to }{A}\right)=-\stackrel{\to }{mg}``
`` \left|vA\,\mathrm{\,sin \,}\theta \right|=\left|mg\right|``
`` \therefore v=\frac{mg}{A\,\mathrm{\,sin \,}\theta }``
v will be minimum when sinθ = 1.
⇒ θ = 90°
`` \therefore {v}_{min}=\frac{mg}{A}``
Page No 80:

Qstn #22
In a simple Atwood machine, two unequal masses m₁ and m₂ are connected by a string going over a clamped light smooth pulley. In a typical arrangement (figure 5-E7), m₁ = 300 g and m₂ = 600 g. The system is released from rest.
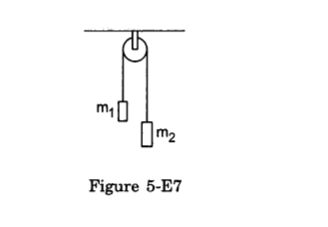Ans : The masses of the blocks are m₁ = 0.3 kg and m₂ = 0.6 kg
The free-body diagrams of both the masses are shown below:

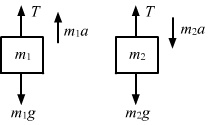
For mass m₁,
T - m₁g = m₁a ...(i)
For mass m₂,
m₂g - T= m₂a ...(ii)
Adding equations (i) and (ii), we get:
g(m₂ - m₁) = a(m₁ + m₂)
`` \Rightarrow a=g\left(\frac{{m}_{2}-{m}_{1}}{{m}_{1}+{m}_{2}}\right)``
`` =9.8\times \frac{0.6-0.3}{0.6+0.3}``
`` =3.266\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``

#22-a
Find the distance travelled by the first block in the first two seconds;
Ans : t = 2 s, a = 3.266 ms^-2, u = 0
So, the distance travelled by the body,
`` \,\mathrm{\,S \,}=ut+\frac{1}{2}a{t}^{2}``
`` =0+\frac{1}{2}\left(3.266\right){2}^{2}=6.5\,\mathrm{\,m \,}``

#22-b
find the tension in the string;
Ans : From equation (i),
T = m₁ (g + a)
= 0.3 (3.8 + 3.26) = 3.9 N

#22-c
find the force exerted by the clamp on the pulley.
Figure
Ans : The force exerted by the clamp on the pulley,
F = 2T = 2 × 3.9 = 7.8 N
Page No 80:

Qstn #23
Consider the Atwood machine of the previous problem. The larger mass is stopped for a moment, 2.0 s after the system is set into motion. Find the time that elapses before the string is tight again.
Ans : a = 3.26 m/s², T = 3.9 N
After 2 s, velocity of mass m₁_,
v = u + at = 0 + 3.26 × 2
= 6.52 m/s upward
At this time, m₂ is moving 6.52 m/s downward.
At time 2 s, m₂ stops for a moment. But m₁ is moving upward with velocity 6.52 m/s. It will continue to move till final velocity (at highest point) becomes zero.
Here, v = 0, u = 6.52 m/s
a = -g = - 9.8 m/s²
v = u + at = 6.52 + (-9.8)t
`` \Rightarrow t=\frac{6.52}{9.8}\approx \frac{2}{3}\,\mathrm{\,sec \,}``
After this time, the mass m₁ also starts moving downward.
So, the string becomes tight again after `` \frac{2}{3}\,\mathrm{\,s \,}``.
Page No 80:

Qstn #24
Figure (5-E8) shows a uniform rod of length 30 cm and mass 3.0 kg. The strings shown in the figure are pulled by constant forces of 20 N and 32 N. Find the force exerted by the 20 cm part of the rod on the 10 cm part. All the surfaces are smooth and the strings and the pulleys are light.
Figure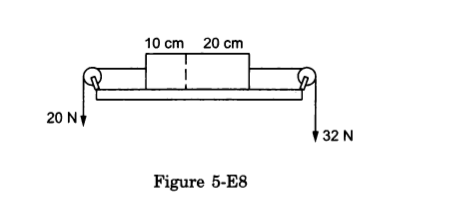
Ans : Mass per unit length`` =\frac{3}{30}\,\mathrm{\,kg \,}/\,\mathrm{\,cm \,}`` = 0.10 kg/cm
Mass of the 10 cm part, m₁ = 1 kg
Mass of the 20 cm part, m₂ = 2 kg
Let F = contact force between them.

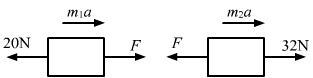
From the free-body diagram,
`` {m}_{1}a=F-20...\left(\,\mathrm{\,i \,}\right)``
`` {m}_{2}a=32-F...\left(\,\mathrm{\,ii \,}\right)``
`` \,\mathrm{\,Adding \,}\,\mathrm{\,both \,}\,\mathrm{\,the \,}\,\mathrm{\,equation \,}\text{ s },\,\mathrm{\,we \,}\,\mathrm{\,get \,}:``
`` a=\frac{12}{{m}_{1}+{m}_{2}}=\frac{12}{3}=4\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
So, contact force,
F = 20 + 1a
F = 20 + 4 = 24 N
Page No 81:

Qstn #25
Consider the situation shown in figure (5-E9). All the surfaces are frictionless and the string and the pulley are light. Find the magnitude of acceleration of the two blocks.
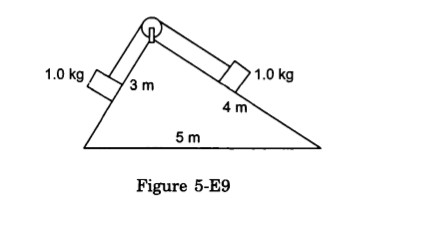Ans : Mass of each block is 1 kg, `` \,\mathrm{\,sin \,}{\,\mathrm{\,\theta \,}}_{1}=\frac{4}{5}``, `` \,\mathrm{\,sin \,}{\,\mathrm{\,\theta \,}}_{2}=\frac{3}{5}``.
The free-body diagrams for both the boxes are shown below:

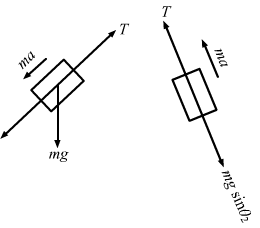
mgsinθ₁ - T = ma ...(i)
T - mgsinθ₂ = ma ...(ii)
Adding equations (i) and (ii),we get:
mg(sinθ₁ - sinθ₂) = 2ma
⇒ 2a = g (sinθ₁ - sinθ₂)
`` \Rightarrow a=\frac{g}{5}\times \frac{1}{2}``
`` =\frac{g}{10}``
Page No 81:

Qstn #26
A constant force F = m₂g/2 is applied on the block of mass m₁ as shown in figure (5-E10). The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m₁.
Figure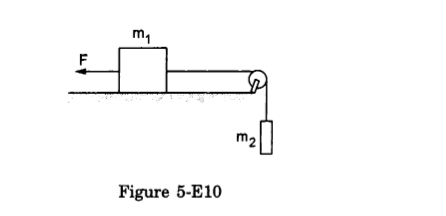
Ans : The free-body diagrams for both the blocks are shown below:

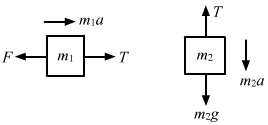
From the free-body diagram of block of mass m₁,
m₁a = T - F ...(i)
From the free-body diagram of block of mass m₂,
m₂a = m₂g - T ...(ii)
Adding both the equations, we get:
`` a\left({m}_{1}+{m}_{2}\right)={m}_{2}g-\frac{{m}_{2}g}{2}\left[\,\mathrm{\,because \,}F=\frac{{m}_{2}g}{2}\right]``
`` \Rightarrow a=\frac{{m}_{2}g}{2\left({m}_{1}+{m}_{2}\right)}``
So, the acceleration of mass m₁,
`` a=\frac{{m}_{2}g}{2\left({m}_{1}+{m}_{2}\right)},\,\mathrm{\,towards \,}\text{ the }\,\mathrm{\,right \,}.``
Page No 81:

Qstn #27
In figure (5-E11), m₁ = 5 kg, m₂ = 2 kg and F = 1 N. Find the acceleration of either block. Describe the motion of m₁ if the string breaks but F continues to act.
Figure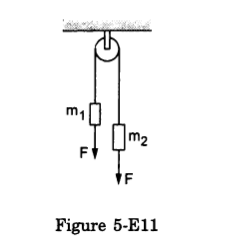
Ans : Let the acceleration of the blocks be a.
The free-body diagrams for both the blocks are shown below:

From the free-body diagram,
m₁a = m₁g + F - T ...(i)
Again, from the free-body diagram,
m₂a = T - m₂g - F ...(ii)
Adding equations (i) and (ii), we have:
`` a=g\frac{{m}_{1}-{m}_{2}}{{m}_{1}+{m}_{2}}``
`` ``
`` \Rightarrow a=\frac{3g}{7}=\frac{29.4}{7}``
`` =4.2\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
Hence, acceleration of the block is 4.2 m/s².
After the string breaks, m₁ moves downward with force F acting downward. Then,

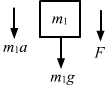
m₁a = F + m₁g
5a = 1 + 5g
`` \Rightarrow a=\frac{5g+1}{5}``
`` =g+0.2\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
Page No 81:

Qstn #28
Let m₁ = 1 kg, m₂ = 2 kg and m₃ = 3 kg in figure (5-E12). Find the accelerations of m₁, m₂ and m₃. The string from the upper pulley to m₁ is 20 cm when the system is released from rest. How long will it take before m₁ strikes the pulley?
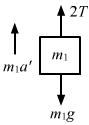
Figure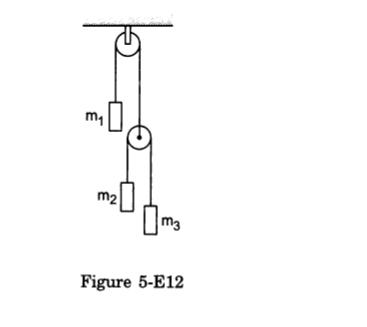
Ans : The free-body diagram for mass m₁ is shown below:

(Figure 1)
The free-body diagram for mass m₂ is shown below:

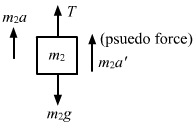
(Figure 2)
The free-body diagram for mass m₃ is shown below:

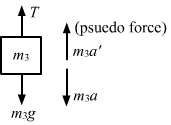
(Figure 3)
Suppose the block m₁ moves upward with acceleration a₁ and the blocks m₂ and m₃ have relative acceleration a₂ due to the difference of weight between them.
So, the actual acceleration of the blocks m₁, m₂ and m₃ will be a₁, (a₁ - a₂) and (a₁ + a₂), as shown.
From figure 2, T - 1g - 1a₁ = 0 ...(i)
From figure 3, `` \frac{T}{2}-2g-2\left({a}_{1}-{a}_{2}\right)=0...\left(\,\mathrm{\,ii \,}\right)``
From figure 4, `` \frac{T}{2}-3g-3\left({a}_{1}+{a}_{2}\right)=0...\left(\,\mathrm{\,iii \,}\right)``
From equations (i) and (ii), eliminating T, we get:
1g + 1a₂ = 4g + 4 (a₁ + a₂)
5a₂ - 4a₁ = 3g ...(iv)
From equations (ii) and (iii), we get:
2g + 2(a₁ - a₂) = 3g - 3 (a₁ - a₂)
5a₁ + a₂ = g ...(v)
Solving equations (iv) and (v), we get:
`` {a}_{1}=\frac{2g}{29}``
`` \,\mathrm{\,and \,}{a}_{2}=g-5{a}_{1}``
`` \Rightarrow {a}_{2}=g-\frac{10g}{29}=\frac{19g}{29}``
`` \,\mathrm{\,So \,},{a}_{1}-{a}_{2}=\frac{2g}{29}-\frac{19g}{29}=-\frac{17g}{29}``
`` \,\mathrm{\,and \,}{a}_{1}+{a}_{2}=\frac{2g}{29}+\frac{19g}{29}=\frac{21g}{29}``
So, accelerations of m₁, m₂ and m₃ are `` \frac{19g}{29}\left(\,\mathrm{\,up \,}\right),\frac{17g}{29}\left(\,\mathrm{\,down \,}\right)\,\mathrm{\,and \,}\frac{21g}{29}\left(\,\mathrm{\,down \,}\right)`` , respectively.
Now, u = 0, s = 20 cm = 0.2 m
`` {a}_{2}=\frac{19g}{29}``
`` \therefore s=ut+\frac{1}{2}a{t}^{2}``
`` \Rightarrow 0.2=\frac{1}{2}\times \frac{19}{29}g{t}^{2}``
`` \Rightarrow t=0.25\,\mathrm{\,s \,}``
Page No 81:

Qstn #29
In the previous problem, suppose m₂ = 2.0 kg and m₃ = 3.0 kg. What should be the mass m, so that it remains at rest?
Ans :
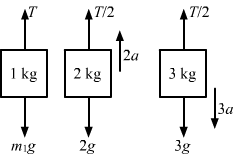
For m₁ to be at rest, a₁= 0.
T - m₁g = 0
T = m₁g ...(i)
For mass m₂,
T/2 - 2g = 2a
T = 4a + 4g ...(ii)
For mass m₃,
3g - T/2= 2a
T = 6g - 6a ...(ii)
From equations (ii) and (iii), we get:
3T - 12g = 12g - 2T
T = 24g/5= 4.08g
Putting the value of T in equation (i), we get:
m₁= 4.8kg
Page No 81: