CBSE-XI-Physics
05: Newton's Laws of Motion
- #26A constant force F = m2g/2 is applied on the block of mass m1 as shown in figure (5-E10). The string and the pulley are light and the surface of the table is smooth. Find the acceleration of m1.
Figure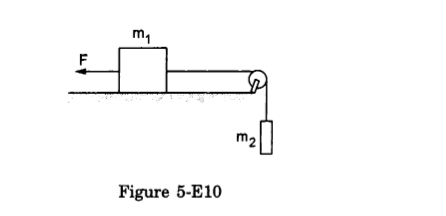
Ans : The free-body diagrams for both the blocks are shown below:
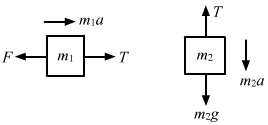
From the free-body diagram of block of mass m1,
m1a = T - F ...(i)
From the free-body diagram of block of mass m2,
m2a = m2g - T ...(ii)
Adding both the equations, we get:
`` a\left({m}_{1}+{m}_{2}\right)={m}_{2}g-\frac{{m}_{2}g}{2}\left[\,\mathrm{\,because \,}F=\frac{{m}_{2}g}{2}\right]``
`` \Rightarrow a=\frac{{m}_{2}g}{2\left({m}_{1}+{m}_{2}\right)}``
So, the acceleration of mass m1,
`` a=\frac{{m}_{2}g}{2\left({m}_{1}+{m}_{2}\right)},\,\mathrm{\,towards \,}\text{ the }\,\mathrm{\,right \,}.``
Page No 81: