HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
CBSE-XI-Physics

05: Newton's Laws of Motion

with Solutions - page 5

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #11
    A small block B is placed on another block A of mass 5 kg and length 20 cm. Initially, the block B is near the right end of block A (Figure 5-E3). A constant horizontal force of 10 N is applied to the block A. All the surfaces are assumed frictionless. Find the time that elapses before block B separates from A.
    Figure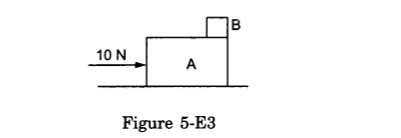
    Ans : Mass of block A, m = 5 kg
    F = ma = 10 N
    `` \Rightarrow a=\frac{10}{5}=2\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
    As there is no friction between A and B, when block A moves, block B remains at rest in its position.
    Initial velocity of A, u = 0
    Distance covered by A to separate out,
    s = 0.2 m
    Using `` s=ut+\frac{1}{2}a{t}^{2}``, we get:
    `` 0.2=0+\frac{1}{2}\times 2{t}^{2}``
    ⇒ t2 = 0.2
    ⇒ t = 0.44 s ≈ 0.45 s
    Page No 79:
  • Qstn #12
    A man has fallen into a ditch of width d and two of his friends are slowly pulling him out using a light rope and two fixed pulleys as shown in figure (5-E4). Show that the force (assumed equal for both the friends) exerted by each friend on the road increases as the man moves up. Find the force when the man is at a depth h.
     
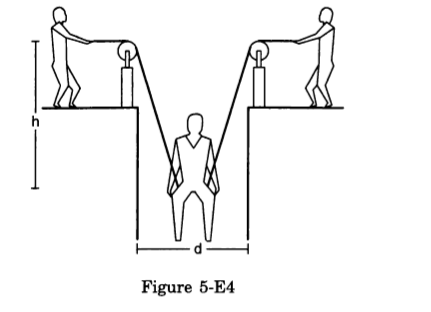    Ans : a) At any depth, let the ropes makes an angle θ with the vertical.

    From the free-body diagram,
    Fcosθ + Fcosθ - mg = 0
    2Fcosθ = mg
    `` \Rightarrow F=\frac{mg}{2cos\theta }``
    As the man moves up, θ increases, i.e. cosθ decreases. Thus, F increases.
    b) When the man is at depth h,
    `` \,\mathrm{\,cos \,}\theta =\frac{h}{\sqrt{{\left(d/2\right)}^{2}+{h}^{2}}}``
    `` F=\frac{mg}{2\,\mathrm{\,cos \,}\theta }``
    `` =\frac{mg}{2\left[h/\sqrt{{\left({\displaystyle \frac{d}{2}}\right)}^{2}+{h}^{2}}\right]}``
    `` =\frac{mg}{4h}\sqrt{{d}^{2}+4{h}^{2}}``
    Page No 80:
  • Qstn #13
    The elevator shown in figure (5-E5) is descending with an acceleration of 2 m/s2. The mass of the block A is 0.5 kg. What force is exerted by the block A on the block B?
    Figure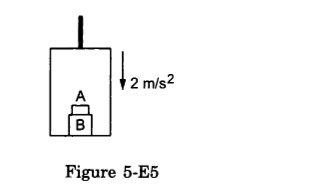
    Ans : When the elevator is descending, a pseudo-force acts on it in the upward direction, as shown in the figure.

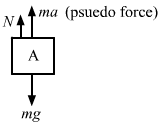
    From the free-body diagram of block A,
    `` mg-N=ma``
    `` N=m\left(g-a\right)``
    `` \Rightarrow N=0.5\left(10-2\right)=4\,\mathrm{\,N \,}``
    `` ``
    So, the force exerted by the block A on the block B is 4 N.
    Page No 80:
  • Qstn #14
    A pendulum bob of mass 50 g is suspended from the ceiling of an elevator. Find the tension in the string if the elevator
  • #14-a
    goes up with acceleration 1.2 m/s2,
    Ans : When the elevator goes up with acceleration 1.2 m/s2:

    `` T=mg+ma``
    ⇒ T = 0.05 (9.8 + 1.2) = 0.55 N
  • #14-b
    goes up with deceleration 1.2 m/s2,
    Ans : Goes up with deceleration 1.2 m/s2 :

    `` T=mg+m\left(-a\right)=m\left(g-a\right)``
    ⇒ T = 0.05 (9.8 - 1.2) = 0.43 N
  • #14-c
    goes up with uniform velocity,
    Ans : Goes up with uniform velocity:

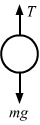
    `` T=mg``
    ⇒ T = 0.05 × 9.8 = 0.49 N
  • #14-d
    goes down with acceleration 1.2 m/s2,
    Ans : Goes down with acceleration 1.2 m/s2 :

    `` T+ma=mg``
    `` \Rightarrow T=m\left(g-a\right)``
    ⇒ T = 0.05 (9.8 - 1.2) = 0.43 N
  • #14-e
    goes down with deceleration 1.2 m/s2 and
    Ans : Goes down with deceleration 1.2 m/s2 :

    `` T+m\left(-a\right)=mg``
    `` \Rightarrow T=m\left(g+a\right)``
    ⇒ T = 0.05 (9.8 + 1.2) = 0.55 N
  • #14-f
    goes down with uniform velocity.
    Ans : Goes down with uniform velocity:

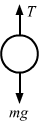
    `` T=mg``
    ⇒ T = 0.05 × 9.8 = 0.49 N
    Page No 80:
  • Qstn #15
    A person is standing on a weighing machine placed on the floor of an elevator. The elevator starts going up with some acceleration, moves with uniform velocity for a while and finally decelerates to stop. The maximum and the minimum weights recorded are 72 kg and 60 kg, respectively. Assuming that the magnitudes of acceleration and deceleration are the same, find
    Ans :
    Maximum weight will be recorded when the elevator accelerates upwards.
    Let N be the normal reaction on the person by the weighing machine.
    So, from the free-body diagram of the person,
    `` N=mg+ma`` ...(1)
    This is maximum weight, N = 72 × 9.9 N
    When decelerating upwards, minimum weight will be recorded.
    `` N\text{ ' }=mg+m\left(-a\right)`` ...(2)
    This is minimum weight, N' = 60 × 9.9 N
    From equations (1) and (2), we have:
    2 mg = 1306.8
    `` \Rightarrow m=\frac{1306.8}{2\times 9.9}=66\,\mathrm{\,kg \,}``
    So, the true mass of the man is 66 kg.
    And true weight = 66 `` \times `` 9.9 = 653.4 N
    (b) Using equation (1) to find the acceleration, we get:
    mg + ma = 72 × 9.9
    `` \Rightarrow a=\frac{72\times 9.9-66\times 9.9}{66}=\frac{9.9\times 6}{66}=\frac{9.9}{11}``
    `` \Rightarrow a=0.9\,\mathrm{\,m \,}/{\,\mathrm{\,s \,}}^{2}``
    Page No 80:
  • #15-a
    the true weight of the person and
    Ans : Maximum weight will be recorded when the elevator accelerates upwards.
    Let N be the normal reaction on the person by the weighing machine.
    So, from the free-body diagram of the person,
    N=mg+ma ...(1)
    This is maximum weight, N = 72 × 9.9 N
    When decelerating upwards, minimum weight will be recorded.
    N’=mg+m-a ...(2)
    This is minimum weight, N‘ = 60 × 9.9 N
    From equations (1) and (2), we have:
    2 mg = 1306.8
    ⇒m=1306.82×9.9=66 kg
    So, the true mass of the man is 66 kg.
    And true weight = 66
    ×9.9 = 653.4 N
  • #15-b
    the magnitude of the acceleration. Take g = 9.9 m/s2.
    Figure
    Ans : Using equation (1) to find the acceleration, we get:
    mg + ma = 72 × 9.9
    ⇒a=72×9.9-66×9.966=9.9×666=9.911⇒a=0.9 m/s2
  • Qstn #16
    Find the reading of the spring balance shown in figure (5-E6). The elevator is going up with an acceleration g/10, the pulley and the string are light and the pulley is smooth.
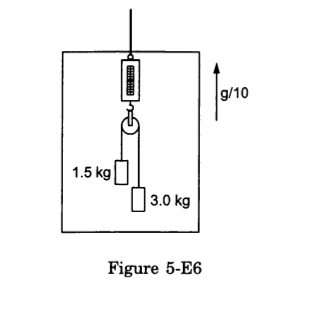    Ans : Let the left and right blocks be A and B, respectively.
    And let the acceleration of the 3 kg mass relative to the elevator be 'a' in the downward direction.

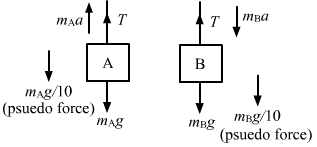
    From the free-body diagram,
    `` {m}_{A}a=T-{m}_{A}g-\frac{{m}_{A}g}{10}...\left(1\right)``
    `` {m}_{B}a={m}_{B}g+\frac{{m}_{B}g}{10}-T...\left(2\right)``
    Adding both the equations, we get:
    `` a\left({m}_{A}+{m}_{B}\right)=\left({m}_{B}-{m}_{A}\right)g+\left({m}_{B}-{m}_{A}\right)\frac{g}{10}``
    Putting value of the masses,we get:
    `` 9a=\frac{33g}{10}``
    `` \Rightarrow \frac{a}{g}=\frac{11}{30}...\left(3\right)``
    Now, using equation (1), we get:
    `` T={m}_{A}\left(a+g+\frac{g}{10}\right)``
    The reading of the spring balance = `` \frac{2T}{g}=\frac{2}{g}{m}_{A}\left(a+g+\frac{g}{10}\right)``
    `` \Rightarrow 2\times 1.5\left(\frac{a}{g}+1+\frac{1}{10}\right)=3\left(\frac{11}{30}+1+\frac{1}{10}\right)``
    `` =4.4\,\mathrm{\,kg \,}``
    Page No 80:
  • Qstn #17
    A block of 2 kg is suspended from a ceiling by a massless spring of spring constant k = 100 N/m. What is the elongation of the spring? If another 1 kg is added to the block, what would be the further elongation?
    Ans : Given,
    mass of the first block, m = 2 kg
    k = 100 N/m
    Let elongation in the spring be x.

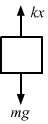
    From the free-body diagram,
    kx = mg
    `` x=\frac{mg}{k}=\frac{2\times 9.8}{100}``
    `` =\frac{19.6}{100}=0.196\approx 0.2\,\mathrm{\,m \,}``
    Suppose, further elongation, when the 1 kg block is added, is `` ∆x``.
    Then,`` k\left(x+∆x\right)=m\text{ ' }g``
    ⇒ k`` ∆x``= 3g - 2g = g
    `` \Rightarrow ∆x=\frac{g}{k}=\frac{9.8}{100}=0.098\approx 0.1\,\mathrm{\,m \,}``
    Page No 80:
next page