CBSE-XI-Physics
05: Newton's Laws of Motion
- #16Find the reading of the spring balance shown in figure (5-E6). The elevator is going up with an acceleration g/10, the pulley and the string are light and the pulley is smooth.
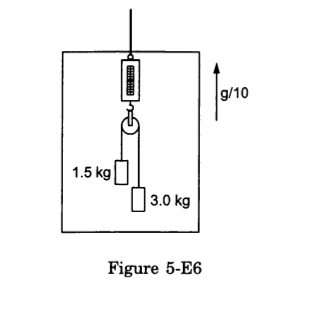Ans : Let the left and right blocks be A and B, respectively.
And let the acceleration of the 3 kg mass relative to the elevator be 'a' in the downward direction.
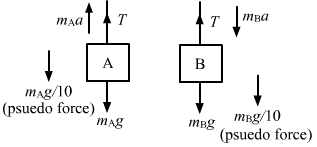
From the free-body diagram,
`` {m}_{A}a=T-{m}_{A}g-\frac{{m}_{A}g}{10}...\left(1\right)``
`` {m}_{B}a={m}_{B}g+\frac{{m}_{B}g}{10}-T...\left(2\right)``
Adding both the equations, we get:
`` a\left({m}_{A}+{m}_{B}\right)=\left({m}_{B}-{m}_{A}\right)g+\left({m}_{B}-{m}_{A}\right)\frac{g}{10}``
Putting value of the masses,we get:
`` 9a=\frac{33g}{10}``
`` \Rightarrow \frac{a}{g}=\frac{11}{30}...\left(3\right)``
Now, using equation (1), we get:
`` T={m}_{A}\left(a+g+\frac{g}{10}\right)``
The reading of the spring balance = `` \frac{2T}{g}=\frac{2}{g}{m}_{A}\left(a+g+\frac{g}{10}\right)``
`` \Rightarrow 2\times 1.5\left(\frac{a}{g}+1+\frac{1}{10}\right)=3\left(\frac{11}{30}+1+\frac{1}{10}\right)``
`` =4.4\,\mathrm{\,kg \,}``
Page No 80: