NEET-XII-Chemistry
04: Chemical Kinetics
- #15-iPlot [N2O5] against t.
() Find the half-life period for the reaction.
() Draw a graph between log [N2O5] and t.
() What is the rate law?
() Calculate the rate constant.
() Calculate the half-life period from k and compare it with (ii).
() Find the half-life period for the reaction.
() Draw a graph between log [N2O5] and t.
() What is the rate law?
() Calculate the rate constant.
() Calculate the half-life period from k and compare it with (ii).
() Find the half-life period for the reaction.
() Draw a graph between log [N2O5] and t.
() What is the rate law?
() Calculate the rate constant.
() Calculate the half-life period from k and compare it with (ii).Ans :
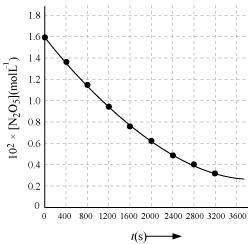
() Time corresponding to the concentration, is the half life. From the graph, the half life is obtained as 1450 s.
is the half life. From the graph, the half life is obtained as 1450 s.
()-
t(s)
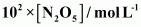
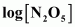
0
1.63
- 1.79
400
1.36
- 1.87
800
1.14
- 1.94
1200
0.93
- 2.03
1600
0.78
- 2.11
2000
0.64
- 2.19
2400
0.53
- 2.28
2800
0.43
- 2.37
3200
0.35
- 2.46
() The given reaction is of the first order as the plot,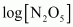 v/s t, is a straight line. Therefore, the rate law of the reaction is
v/s t, is a straight line. Therefore, the rate law of the reaction is
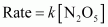
() From the plot,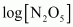 v/s t, we obtain
v/s t, we obtain
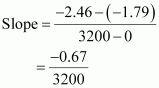
Again, slope of the line of the plot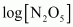 v/s t is given by
v/s t is given by
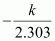 .
.
Therefore, we obtain,
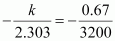

() Half-life is given by,
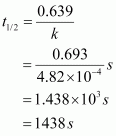
This value, 1438 s, is very close to the value that was obtained from the graph.
() Time corresponding to the concentration, is the half life. From the graph, the half life is obtained as 1450 s.
is the half life. From the graph, the half life is obtained as 1450 s.
()-
t(s)
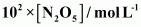
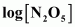
0
1.63
- 1.79
400
1.36
- 1.87
800
1.14
- 1.94
1200
0.93
- 2.03
1600
0.78
- 2.11
2000
0.64
- 2.19
2400
0.53
- 2.28
2800
0.43
- 2.37
3200
0.35
- 2.46

() The given reaction is of the first order as the plot,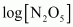 v/s t, is a straight line. Therefore, the rate law of the reaction is
v/s t, is a straight line. Therefore, the rate law of the reaction is
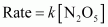
() From the plot,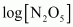 v/s t, we obtain
v/s t, we obtain
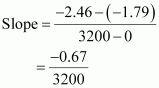
Again, slope of the line of the plot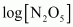 v/s t is given by
v/s t is given by
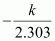 .
.
Therefore, we obtain,
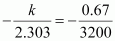

() Half-life is given by,
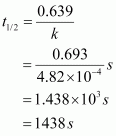
This value, 1438 s, is very close to the value that was obtained from the graph.
() Time corresponding to the concentration, is the half life. From the graph, the half life is obtained as 1450 s.
is the half life. From the graph, the half life is obtained as 1450 s.
()-
t(s)
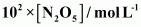
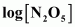
0
1.63
- 1.79
400
1.36
- 1.87
800
1.14
- 1.94
1200
0.93
- 2.03
1600
0.78
- 2.11
2000
0.64
- 2.19
2400
0.53
- 2.28
2800
0.43
- 2.37
3200
0.35
- 2.46

() The given reaction is of the first order as the plot,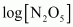 v/s t, is a straight line. Therefore, the rate law of the reaction is
v/s t, is a straight line. Therefore, the rate law of the reaction is
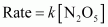
() From the plot,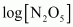 v/s t, we obtain
v/s t, we obtain
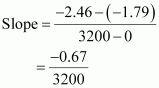
Again, slope of the line of the plot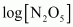 v/s t is given by
v/s t is given by
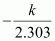 .
.
Therefore, we obtain,
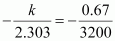

() Half-life is given by,
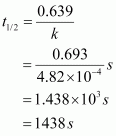
This value, 1438 s, is very close to the value that was obtained from the graph.
-
- #15-iiFind the half-life period for the reaction.Ans : Time corresponding to the concentration,
 is the half life. From the graph, the half life is obtained as 1450 s.
is the half life. From the graph, the half life is obtained as 1450 s.
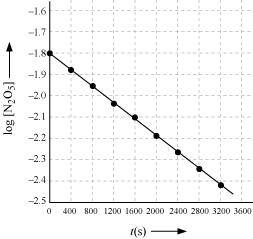
- #15-iiiDraw a graph between log [N2O5] and t.Ans :
-
t(s)
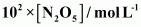
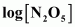
0
1.63
- 1.79
400
1.36
- 1.87
800
1.14
- 1.94
1200
0.93
- 2.03
1600
0.78
- 2.11
2000
0.64
- 2.19
2400
0.53
- 2.28
2800
0.43
- 2.37
3200
0.35
- 2.46

-
- #15-ivWhat is the rate law?Ans : The given reaction is of the first order as the plot,
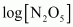 v/s t, is a straight line. Therefore, the rate law of the reaction is
v/s t, is a straight line. Therefore, the rate law of the reaction is
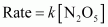
- #15-vCalculate the rate constant.Ans : From the plot,
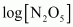 v/s t, we obtain
v/s t, we obtain
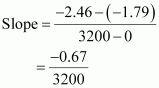
Again, slope of the line of the plot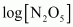 v/s t is given by
v/s t is given by
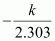 .
.
Therefore, we obtain,
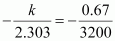

- #15-viCalculate the half-life period from k and compare it with (ii).Ans : Half-life is given by,
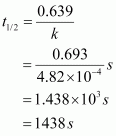
This value, 1438 s, is very close to the value that was obtained from the graph.