NEET-XII-Physics
11: Gravitation
- #3-athe mid-point of a side, (b) at the centre of the triangle.Ans : Consider that mass 'm' is placed at the midpoint O of side AB of equilateral triangle ABC.
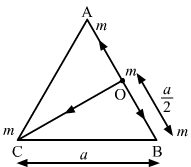
AO = BO = `` \frac{a}{2}``
Then `` {\stackrel{\to }{F}}_{\,\mathrm{\,OA\,}}=\frac{4\,\mathrm{\,G\,}{m}^{2}}{{a}^{2}}`` along OA
Also, `` {\stackrel{\to }{F}}_{\,\mathrm{\,OB\,}}=\frac{4\,\mathrm{\,G\,}{m}^{2}}{{a}^{2}}`` along OB
OC = `` \frac{\sqrt{3}a}{2}``
`` {\stackrel{\to }{F}}_{\,\mathrm{\,OC\,}}=\frac{4\,\mathrm{\,G\,}{m}^{2}}{\left\{\left(3\right){a}^{2}\right\}}=\frac{4G{m}^{2}}{3{a}^{2}}`` along OC
The net force on the particle at O is `` \stackrel{\to }{F}={\stackrel{\to }{F}}_{\,\mathrm{\,OA\,}}+{\stackrel{\to }{F}}_{\,\mathrm{\,OB\,}}+{\stackrel{\to }{F}}_{\,\mathrm{\,OC\,}}``.
Since equal and opposite forces cancel each other, we have:
`` \stackrel{\to }{F}={\stackrel{\to }{F}}_{\,\mathrm{\,OC\,}}=\frac{4\,\mathrm{\,G\,}{m}^{2}}{\left\{\left(3\right){a}^{2}\right\}}=\frac{4G{m}^{2}}{3{a}^{2}}`` along OC. (b) If the particle placed at O (centroid)
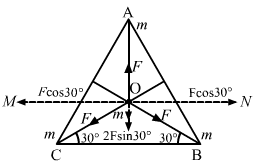
All the forces are equal in magnitude but their directions are different as shown in the figure.
Equal and opposite forces along OM and ON cancel each other.
i.e., `` F\,\mathrm{\,cos\,}30°=F\,\mathrm{\,cos\,}30°``
∴ Resultant force `` =F-2F\,\mathrm{\,sin\,}30=0``
Page No 226:
- #3-bat the centre of the triangle.Ans : If the particle placed at O (centroid)

All the forces are equal in magnitude but their directions are different as shown in the figure.
Equal and opposite forces along OM and ON cancel each other.
i.e., `` F\,\mathrm{\,cos\,}30°=F\,\mathrm{\,cos\,}30°``
∴ Resultant force `` =F-2F\,\mathrm{\,sin\,}30=0``
Page No 226: