HomeLearn Fast select Course
Change UnitChange SubjectLast Menu
NEET-XII-Physics

10: Rotational Mechanics

with Solutions - page 4

Note: Please signup/signin free to get personalized experience.

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

  
  • Qstn #21
    A wheel of radius 20 cm is pushed to move it on a rough horizontal surface. If is found to move through a distance of 60 cm on the road during the time it completes one revolution about the centre. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is
    (a) along the velocity of the wheel
    (b) opposite to the velocity of the wheel
    (c) perpendicular to the velocity of the wheel
    (d) zero.
    digAnsr:   a
    Ans : (a) along the velocity of the wheel
    As the distance covered in one revolution about the centre is less than the perimeter of the wheel, it means that the direction of torque due to frictional force opposes the motion of wheel, i.e., the frictional force acting on the wheel by the surface is along the velocity of the wheel.
    FIG.
    Page No 194:
  • Qstn #22
    The angular velocity of the engine (and hence of the wheel) of a scooter is proportional to the petrol input per second. The scooter is moving on a frictionless road with uniform velocity. If the petrol input is increased by 10%, the linear velocity of the scooter is increased by
    (a) 50%
    (b) 10%
    (c) 20%
    (d) 0%.
    digAnsr:   d
    Ans : (d) 0%.
    On a frictionless road, we have:
    Angular velocity of the engine = 0
    Therefore, increase in petrol input will not affect the angular velocity and hence the linear velocity of the scooter will remain the same.
    Page No 194:
  • Qstn #23
    A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of a smooth incline and released. Least time will be taken in reaching the bottom by
    (a) the solid sphere
    (b) the hollow sphere
    (c) the disc
    (d) all will take same time.
    digAnsr:   d
    Ans : (d) all will take same time.
    The incline is smooth; therefore, all bodies will slip on the incline. Also, as the mass of bodies is same, they will reach the bottom in equal time.
    Page No 194:
  • Qstn #24
    A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top on an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by
    (a) the solid sphere
    (b) the hollow sphere
    (c) the disc
    (d) all will take same time.
    digAnsr:   d
    Ans : (d) all will take same time
    Let θ be the inclination angle.

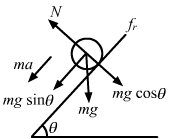
    From the free body diagram, we have:
    `` N=mg\,\mathrm{\,cos\,}\theta ...\left(i\right)``
    `` ma=mg\,\mathrm{\,sin\,}\theta -{f}_{r}...\left(ii\right)``
    `` \,\mathrm{\,Putting\,}{f}_{r}=\mu N\,\mathrm{\,in\,}\left(ii\right)weget,``
    `` a=g\left(\,\mathrm{\,sin\,}\theta -\mu \,\mathrm{\,cos\,}\theta \right)``
    `` ``
    `` ``
    The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling; therefore, all the bodies come down with the same acceleration.
    Page No 194:
  • Qstn #25
    In the previous question, the smallest kinetic energy at the bottom of the incline will be achieved by
    (a) the solid sphere
    (b) the hollow sphere
    (c) the disc
    (d) all will achieve same kinetic energy.
    digAnsr:   b
    Ans : (b) the hollow sphere
    Torque is same for all the bodies; therefore, the angular momentum will be conserved.
    Now, total kinetic energy = `` \frac{1}{2}m{v}^{2}+\frac{{L}^{2}}{2I}``
    So, the body with greater value of moment of inertia will have smallest kinetic energy at the bottom of the incline.
    Order of the moment of inertia of the bodies:
    hollow sphere > disc > solid sphere
    Hence, the hollow sphere will have the smallest kinetic energy at the bottom.
    Page No 194:
  • Qstn #26
    A string of negligible thickness is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the string and pulls the cylinder towards him (figure 10-Q4). There is no slipping anywhere. The length of the string passed through the hand of the man while the cylinder reaches his hands is
    (a) l
    (b) 2l
    (c) 3l
    (d) 4l.
    Figure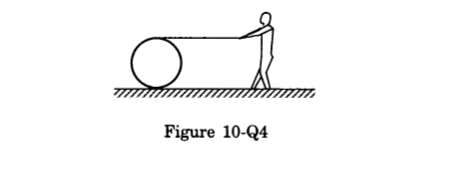
    digAnsr:   b
    Ans : (b) 2l
    For pure rolling, `` \omega r={v}_{0}``
    Figure:
    As shown in the figure, the velocity of the string will be resultant of v0 and ωr.
    `` {v}_{net}={v}_{0}+\left(\omega r\right)``
    `` {v}_{net}=2{v}_{0}``
    Let:
    Linear distance travelled by the cylinder in time (t), `` {v}_{0}t=l``
    ∴ Linear distance travelled by the string in same time, `` 2{v}_{0}t=2l``
    Page No 194:
  • #
    Section : iii
  • Qstn #1
    The axis of rotation of a purely rotating body
    (a) must pass through the centre of mass
    (b) may pass through the centre of mass
    (c) must pass through a particle of the body
    (d) may pass through a particle of the body.
    digAnsr:   b,d
    Ans : (b) may pass through the centre of mass
    (d) may pass through a particle of the body
    It is not necessary that the axis of rotation of a purely rotating body should pass through the centre of mass or through a particle of the body. It can also lie outside the body.
    Page No 194:
  • Qstn #2
    Consider the following two equations
    (A)
    L=I ω(B)
    dLdt=ΓIn noninertial frames
    (a) both A and B are true
    (b) A is true but B is false
    (c) B is true but A is false
    (d) both A and B are false.
    digAnsr:   b,B
    Ans : (b) A is true but B is false.
    In non-inertial frames, `` \frac{dL}{dt}={\Gamma }_{\,\mathrm{\,total\,}}``
    Here, `` {\Gamma }_{\,\mathrm{\,total\,}}`` is is the total torque on the system due to all the external forces acting on the system. So, equation (B) is not true as in non-inertial frames, pseudo force must be applied to study the motion of the object.
    Page No 194:
  • Qstn #3
    A particle moves on a straight line with a uniform velocity. Its angular momentum
    (a) is always zero
    (b) is zero about a point on the straight line
    (c) is not zero about a point away from the straight line
    (d) about any given point remains constant.
    digAnsr:   b,c,d
    Ans : (b) is zero about a point on the straight line
    (c) is not zero about a point away from the straight line
    (d) about any given point remains constant
    (b) Angular momentum = `` m\left(\stackrel{\to }{r}\times \stackrel{\to }{v}\right)``
    If the point is on the straight line, `` \stackrel{\to }{r}\,\mathrm{\,and\,}\stackrel{\mathit{\to }}{\mathit{v}}`` will have the same direction and their cross product will be zero. Hence, angular momentum is zero.
    (c) If the point is not on the straight line, `` \stackrel{\to }{r}\,\mathrm{\,and\,}\stackrel{\mathit{\to }}{\mathit{v}}`` will not have the same direction and their cross product will not be zero. Hence, angular momentum is non-zero.
    (d) No external torque is applied on the body; therefore, its angular momentum about any given point remains constant.
    Page No 194:
  • Qstn #4
    If there is no external force acting on a nonrigid body, which of the following quantities must remain constant?
    (a) angular momentum
    (b) linear momentum
    (c) kinetic energy
    (d) moment of inertia.
    digAnsr:   a,b
    Ans : (a) angular momentum
    (b) linear momentum
    `` {\stackrel{\to }{F}}_{ext}=0``
    `` \Rightarrow {\stackrel{\to }{\tau }}_{ext}=0``
    `` ``
    That is, the change in linear momentum and angular momentum is zero. This is because:
    `` \frac{\mathit{d}\stackrel{\mathit{\to }}{P}}{\mathit{d}t}\mathit{=}{\stackrel{\mathit{\to }}{F}}_{\,\mathrm{\,ext\,}}``
    `` \,\mathrm{\,And\,}\frac{\mathit{d}\stackrel{\mathit{\to }}{L}}{\mathit{d}t}={\stackrel{\to }{\tau }}_{\,\mathrm{\,ext\,}}``
    Page No 194:
  • Qstn #5
    Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
    (a) IA < IB
    (b) If IA < IB, the axes are parallel
    (c) If the axes are parallel, IA < IB
    (d) If the axes are not parallel, IA ≥ IB.
    digAnsr:   c
    Ans : (c) If the axes are parallel, IA < IB
    If axes A and B are parallel, we get:
    `` {I}_{\,\mathrm{\,B\,}}={I}_{\,\mathrm{\,A\,}}+m{r}^{2}``
    Here, r is the distance between two axes and m is the mass of the body.
    `` \therefore `` IA < IB
    Page No 194:
  • Qstn #6
    A sphere is rotating about a diameter.
    (a) The particles on the surface of the sphere do not have any linear acceleration.
    (b) The particles on the diameter mentioned above do not have any linear acceleration.
    (c) Different particles on the surface have different angular speeds.
    (d) All the particles on the surface have same linear speed.
    digAnsr:   b,c,d
    Ans : (b) The particles on the diameter mentioned above do not have any linear acceleration.
    Explanation:
    Linear acceleration of a rotating particle is given as:
    `` \stackrel{\to }{a}=\stackrel{\to }{r}\times \stackrel{\to }{\alpha }``
    (b)
    The sphere is rotating about a diameter; therefore, the position vector of the particles on the diameter is zero. Thus, linear acceleration of the particle is zero.
    (c) and
    (d)
    All the particles of the body have the same angular velocity. All the particle on the surface have different linear speeds that depend on the position of the particle from the axis of rotation.
    Page No 195:
    Page No 195:
  • Qstn #7
    The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis though the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are
    (a) angular acceleration
    (b) angular velocity when the rod completes one rotation
    (c) angular momentum when the rod completes one rotation
    (d) torque of the applied force.
    digAnsr:   d
    Ans : (d) torque of the applied force
    The torque of the applied force does not depend on the density of a rod. It depend on the distance between the pivot and the point where F is applied. So, it does not depend on which end of the rod is pivoted.
    Page No 195:
  • Qstn #8
    Consider a wheel of a bicycle rolling on a level road at a linear speed
    ν0(figure 10-Q5).
    (a) the speed of the particle A is zero
    (b) the speed of B, C and D are all equal to
    v0
    (c) the speed of C is 2
    v0
    (d) the speed of B is greater than the speed of O.
    Figure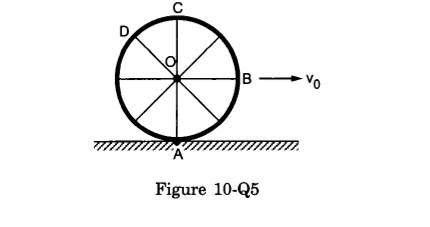
    digAnsr:   a,c,d
    Ans : (a) the speed of the particle A is zero
    (c) the speed of C is 2 `` {v}_{0}``
    (d) the speed of B is greater than the speed of O
    For pure rolling, `` \omega r={v}_{0}``
    Velocity of the particle at A, B, C and D will be resultant of v0 and ωr.

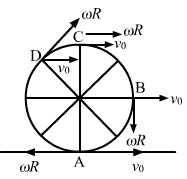
    At point B,
    `` {v}_{net}=\sqrt{{{v}_{0}}^{2}+{\left(\omega r\right)}^{2}}``
    `` {v}_{net}=\sqrt{{{v}_{0}}^{2}+{{v}_{0}}^{2}}``
    `` {v}_{net}=\sqrt{2}{v}_{0}``
    At point C,
    `` {v}_{net}={v}_{0}+\left(\omega r\right)``
    `` {v}_{net}=2{v}_{0}``
    At point A,
    `` {v}_{net}={v}_{0}-\left(\omega r\right)``
    `` {v}_{net}=0``
    At point O,
    r = 0
    `` \therefore {v}_{net}={v}_{0}``
    Page No 195:
next page