NEET-XII-Physics
38: Electromagnetic Induction
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- Qstn #8A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s-1. The normal to the coil makes an angle of 60° with the field. FindAns : Given:
Area of the coil, A = 5 cm2 = 5 × 10-4 m2
The magnetic field at time t is given by
B = B0 sin ωt = 0.2 sin (300t)
Angle of the normal of the coil with the magnetic field, θ = 60°
- #8-athe maximum emf induced in the coil,Ans : The emf induced in the coil is given by
`` e=\frac{-d\theta }{dt}=\frac{d}{dt}(BA\,\mathrm{\,cos\,}\theta )``
`` =\frac{d}{dt}\left[\left({B}_{0}\,\mathrm{\,sin\,}\,\mathrm{\,\omega \,}t\right)\times 5\times {10}^{-4}\times 1/2\right]``
`` ={B}_{0}\times \frac{5}{2}\times {10}^{-4}\frac{d}{dt}(\,\mathrm{\,sin\,}\,\mathrm{\,\omega \,}t)``
`` =\frac{{B}_{0}5}{2}{10}^{-4}\omega \left(\,\mathrm{\,cos\,}\,\mathrm{\,\omega \,}t\right)``
`` =\frac{0.2\times 5}{2}\times 300\times {10}^{-4}\times \,\mathrm{\,cos\,}\,\mathrm{\,\omega \,}t``
`` =15\times {10}^{-3}\,\mathrm{\,cost\,}\,\mathrm{\,\omega \,}t``
The induced emf becomes maximum when cos ωt becomes maximum, that is, 1.
Thus, the maximum value of the induced emf is given by
`` {e}_{max}=15\times {10}^{-3}=0.015\,\mathrm{\,V\,}``
- #8-bthe emf induced at τ = (π/900)s andAns : The induced emf at t = `` \left(\frac{\,\mathrm{\,\pi \,}}{900}\right)\,\mathrm{\,s\,}`` is given by
e = 15 × 10-3 × cos ωt
= 15 × 10-3 × cos `` \left(300\times \frac{\,\mathrm{\,\pi \,}}{900}\right)``
= 15 × 10-3 × `` \frac{1}{2}``
`` =\frac{0.015}{2}=0.0075=7.5\times {10}^{-3}\,\mathrm{\,V\,}``
- #8-cthe emf induced at t = (π/600) s.Ans : The induced emf at t = `` \frac{\,\mathrm{\,\pi \,}}{600}\,\mathrm{\,s\,}`` is given by
e = 15 × 10-3 × cos `` \left(300\times \frac{\,\mathrm{\,\pi \,}}{600}\right)``
= 15 × 10-3 × 0 = 0 V
Page No 306:
- Qstn #9Figure shows a conducting square loop placed parallel to the pole-faces of a ring magnet. The pole-faces have an area of 1 cm2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?
FigureAns : It is given that the magnitude of the magnetic field is 0.10 T and it is perpendicular to the area of the loop.
Also,
Area of the loop, A = 1 cm2 = 10-4 m
Time taken to remove the magnet completely, T = 2 s
Initial magnetic flux, ϕ = `` \stackrel{\to }{B}.\stackrel{\to }{A}`` = BA cos(0) = 10-1 × 10-4 × 1 = 10-5
Now, the induced emf in the magnetic field is given by
`` e=-\frac{∆\,\mathrm{\,\varphi \,}}{∆t}=\frac{{10}^{-5}-0}{1}={10}^{-5}=10\,\mathrm{\,\mu V\,}``
Page No 306:
- Qstn #10A conducting square loop having edges of length 2.0 cm is rotated through 180° about a diagonal in 0.20 s. A magnetic field B exists in the region which is perpendicular to the loop in its initial position. If the average induced emf during the rotation is 20 mV, find the magnitude of the magnetic field.Ans : Given:
Induced emf, e = 20 mV = 20 × 10-3 V
Area of the loop, A = (2 × 10-2)2 = 4 × 10-4 m2
Time taken to rotate the loop, Δt = 0.2 s
The average induced emf is given by
`` e=-\frac{∆\varphi }{∆t}=\frac{{\varphi }_{i}-{\varphi }_{f}}{t}``
`` \varphi =\stackrel{\to }{B}.\stackrel{\to }{A}=BA\,\mathrm{\,cos\,}\theta ``
`` {\varphi }_{i}=B(4\times {10}^{-4})\,\mathrm{\,cos\,}0=B(4\times {10}^{-4})``
`` {\varphi }_{f}=B(4\times {10}^{-4})\,\mathrm{\,cos\,}{180}^{\,\mathrm{\,o\,}}=-B(4\times {10}^{-4})``
`` e=\frac{B(4\times {10}^{-4})-\left[-B(4\times {10}^{-4})\right]}{0.2}``
`` 20\times {10}^{-3}=\frac{8B\times {10}^{-4}}{2\times {10}^{-1}}``
`` \Rightarrow 20\times {10}^{-3}=4\times B\times {10}^{-3}``
`` \Rightarrow B=\frac{20\times {10}^{-3}}{4\times {10}^{-3}}=5\,\mathrm{\,T\,}``
Page No 306:
- Qstn #11A conducting loop of face-area A and resistance R is placed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross-section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.Ans : The magnetic flux through the coil is given by
ϕ = B.A = BA cos 0° = BA
It is given that the loop is withdrawn from the magnetic field.
∴ Final flux = 0
The average induced emf is given by
`` e=-\frac{∆\,\mathrm{\,\varphi \,}}{∆t}=\frac{\,\mathrm{\,BA\,}-0}{t}=\frac{BA}{t}``
`` ``
The current in the loop is given by
`` i=\frac{e}{R}=\frac{BA}{tR}``
The charge flowing through the area of the cross section of the wire is given by
`` q=it=\frac{BA}{R}``
Page No 306:
- Qstn #12radiuA long solenoid ofs 2 cm has 100 turns/cm and carries a current of 5 A. A coil of radius 1 cm having 100 turns and a total resistance of 20 Ω is placed inside the solenoid coaxially. The coil is connected to a galvanometer. If the current in the solenoid is reversed in direction, find the charge flown through the galvanometer.Ans : Given:
Radius of the solenoid, r = 2 cm = 2 × 10-2 m
Number of turns per centimetre, n = 100 = 10000 turns/m
Current flowing through the coil, i = 5 A
The magnetic field through the solenoid is given by
B = μ0ni = 4π × 10-7 × 10000 × 5
= 20π × 10-3 T
Flux linking with per turn of the second solenoid = Bπr2 = Bπ × 10-4
Total flux linking the second coil, ϕ1 = Bn2πr2
∴ ϕ1 = 100 × π × 10-4 × 20π × 10-3
When the direction of the current is reversed, the total flux linking the second coil is given by
ϕ2 = -Bn2πr2
= -(100 × π × 10-4 × 20π × 10-3 )
The change in the flux through the second coil is given by
Δϕ = ϕ2 - ϕ1
= 2 × (100 × π × 10-4 × 20π × 10-3)
Now,
`` e=\frac{∆\,\mathrm{\,\varphi \,}}{∆t}=\frac{4{\,\mathrm{\,\pi \,}}^{2}\times {10}^{-4}}{∆t}``
`` ``
The current through the solenoid is given by
`` I=\frac{e}{R}=\frac{4{\,\mathrm{\,\pi \,}}^{2}\times {10}^{-4}}{∆t\times 20}``
The charge flown through the galvanometer is given by
`` q=I∆t=\frac{4{\,\mathrm{\,\pi \,}}^{2}\times {10}^{-4}}{20\times dt}\times ∆t``
`` =2\times {10}^{-4}\,\mathrm{\,C\,}``
Page No 306:
- Qstn #13Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u.Ans :
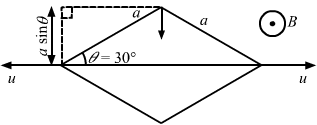
- #13-aFind the induced emf in the frame at the instant when the angles at these corners reduce to 60°.Ans : The effective length of each side is the length that is perpendicular to the velocity of the corners.
Thus, the effective length of each side is a sin θ.
Net effective length for four sides = 4 × `` \frac{a}{2}`` = 2a
∴ Induced emf = Bvl = 2Bau
- #13-bFind the induced current in the frame at this instant if the total resistance of the frame is R.Ans : Current in the frame is given by
i `` =\frac{e}{R}=\frac{2auB}{R}``
- #13-cFind the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
FigureAns : Total charge q, which flows through the sides of the frame, is given by
`` q=\frac{∆\varphi }{R}``
Here,
ΔΦ = Change in the flux
R = Resistance of the coil
`` \therefore q=\frac{∆\varphi }{R}``
`` =\frac{B({a}^{2}-0)}{R}``
`` =\frac{B{a}^{2}}{R}``
Page No 307:
- Qstn #14The north pole of a magnet is brought down along the axis of a horizontal circular coil (figure). As a result, the flux through the coil changes from 0.35 weber to 0.85 weber in an interval of half a second. Find the average emf induced during this period. Is the induced current clockwise or anticlockwise as you look into the coil from the side of the magnet ?
FigureAns : Given:
Initial flux, ϕ1 = 0.35 weber
Final flux ϕ2 = 0.85 weber
∴ Δϕ = ϕ2 - ϕ1
= (0.85 - 0.35) weber
= 0.5 weber
Also,
Δt = 0.5 s
The magnitude of the induced emf is given by
`` e=\frac{∆\,\mathrm{\,\varphi \,}}{∆t}=\frac{0.5}{0.5}=1\,\mathrm{\,V\,}``
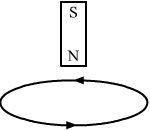
The induced current is anti-clockwise when seen from the side of the magnet.
Page No 307:
- Qstn #15A wire-loop confined in a plane is rotated in its own plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.Ans : When the wire loop is rotated in its own plane in a uniform magnetic field, the magnetic flux through it remains the same. Because there is no change in the magnetic flux, the emf induced in the wire loop is zero.
Page No 307:
- Qstn #16Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop atAns : Given:
Initial velocity, u = 1 cm/s
Magnetic field, B = 0.6 T