NEET-XII-Physics
38: Electromagnetic Induction
Note: Please signup/signin free to get personalized experience.
Note: Please signup/signin free to get personalized experience.
10 minutes can boost your percentage by 10%
Note: Please signup/signin free to get personalized experience.
- #16-at = 2 s,Ans : At t = 2 s:
Distance moved by the coil = 2 × 1 cm/s = 2 cm = 2 × 10`` -``2 m
Area under the magnetic field at t = 2s, A = 2 × 5 × 10`` -``4 m2
Initial magnetic flux = 0
Final magnetic flux = BA = 0.6 × (10 × 10`` -``4) T-m2
Change in the magnetic flux, Δϕ = 0.6 × (10 × 10`` -``4) `` -`` 0
Now, induced emf in the coil is
`` e=\frac{∆\,\mathrm{\,\varphi \,}}{∆t}``
`` =\frac{0.6\times (10-0)\times {10}^{-4}}{2}``
`` =3\times {10}^{-4}\,\mathrm{\,V\,}``
- #16-bt = 10 s,Ans : At t = 10 s:
Distance moved by the coil = 10 × 1 = 10 cm
At this time square loop is completely inside the magnetic field, so there is no change in the flux linked with the coil with time.
Therefore, induced emf in the coil at this time is zero.
- #16-ct = 22 s andAns : At t = 22 s:
Distance moved = 22 × 1 = 22 cm
At this time loop is moving out of the field.
Initial magnetic flux = 0.6 × (5 × 5 × 10`` -``4) T-m
At this time 2 cm part of the loop is ou t of the field.
Therefore, final magnetic flux = 0.6 × (3 × 5 × 10`` -``4) T-m
Change in the magnetic flux, Δϕ = 0.6 × (3 × 5 × 10`` -``4) `` -`` 0.6 × (5 × 5 × 10`` -``4) = `` -``6 × 10`` -``4 T-m2
Now, induced emf is
`` e=\frac{∆\,\mathrm{\,\varphi \,}}{∆t}``
`` =\frac{-6\times {10}^{-4}}{2}``
`` =-3\times {10}^{-4}\,\mathrm{\,V\,}``
- #16-dt = 30 s.
FigureAns : At t = 30 s:
At this time loop is completely out of the field, so there is no change in the flux linked with the coil with time.
Therefore, induced emf in the coil at this time is zero.
Page No 307:
- Qstn #17Find the total heat produced in the loop of the previous problem during the interval 0 to 30 s if the resistance of the loop is 4.5 mΩ.Ans : Resistance of the coil, R = 45 mΩ = 4.5 × 10-3 Ω
The heat produced is found by taking the sum of the individual heats produced.
Thus, the net heat produced is given by
H = H1 + H2 + H3 + H4
(a) Heat developed for the first 5 seconds:
Emf induced, e = 3 × 10-4 V
Current in the coil, `` i=\frac{e}{\,\mathrm{\,R\,}}=\frac{3\times {10}^{-4}}{4.5\times {10}^{-3}}`` = 6.7 × 10-2 A
H1 = (6.7 × 10-2)2 × 4.5 × 10-3 × 5
There is no change in the emf from 5 s to 20 s and from 25 s to 30 s.
Thus, the heat developed for the above mentioned intervals is given by
H2 = H4 = 0
Heat developed in interval t = 25 s to 30 s:
The current and voltage induced in the coil will be the same as that for the first 5 seconds.
H3 = (6.7 × 10-2)2 × 4.5 × 10-3 × 5
Total heat produced:
H = H1 + H3
= 2 × (6.7 × 10-2)2 × 4.5 × 10-2 × 5
= 2 × 10-4 J
Page No 307:
- Qstn #18A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
FigureAns : The magnetic field lines pass through coil abcd only in the part above the cylindrical region.
Radius of the cylindrical region, r = 10 cm
Resistance of the coil, R = 4 Ω
The rate of change of the magnetic field in the cylindrical region is constant and is given by
`` \frac{dB}{dt}=0.010\,\mathrm{\,T\,}/\,\mathrm{\,s\,}``
The change in the magnetic flux is given by
`` \frac{d\,\mathrm{\,\varphi \,}}{dt}=\frac{dB}{dt}A``
`` ``
The induced emf is given by
`` e=\frac{d\,\mathrm{\,\varphi \,}}{dt}=\frac{dB}{dt}\times A=0.01\left(\frac{\,\mathrm{\,\pi \,}\times {r}^{2}}{2}\right)``
`` =\frac{0.01\times 3.14\times 0.01}{2}``
`` =\frac{3.14}{2}\times {10}^{-4}=1.57\times {10}^{-4}\,\mathrm{\,V\,}``
The current in the coil is given by
`` i=\frac{e}{R}=\frac{1.57\times {10}^{-4}}{4}``
`` =0.39\times {10}^{-4}``
`` =3.9\times {10}^{-5}\,\mathrm{\,A\,}``
Page No 307:
- Qstn #19The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00 Ω. Find the current (magnitude and sense) in the wire ad if
- #19-athe switch S1 is closed but S2 is open,Ans : When switch S1 is closed and switch S2 is open:
Rate of change of the magnetic field = 20 mT/s = `` 2\times {10}^{-4}\,\mathrm{\,T\,}/\,\mathrm{\,s\,}``
Net resistance of the coil adef, R = 4 × 4 = 16 Ω
Area of the coil adef = (10-2 )-2 = 10-4 m2
The emf induced is given by
`` e=\frac{d\,\mathrm{\,\varphi \,}}{dt}=\,\mathrm{\,A\,}.\frac{d\,\mathrm{\,B\,}}{dt}``
`` ``
= 10-4 × 2 × 10-2
= 2 × 10-6 V
The current through the wire ad is given by
i`` =\frac{e}{R}=\frac{2\times {10}^{-6}}{16}``
= 1.25 × 10-7 A along ad
- #19-bS1 is open but S2 is closed,Ans : When switch S2 is closed and switch S1 is open:
Net resistance of the coil abcd, R = 16 Ω
The induced emf is given by
`` e=\,\mathrm{\,A\,}\times \frac{d\,\mathrm{\,B\,}}{dt}=2\times {10}^{-6}\,\mathrm{\,V\,}``
The current through wire ad is given by
`` i=\frac{20\times {10}^{-6}}{16}=1.25\times {10}^{-7}\,\mathrm{\,A\,}``
`` `` along da
- #19-cboth S1 and S2 are open andAns : When both S1 and S2 are open, no current is passed, as the circuit is open. Thus, i = 0.
- #19-dboth S1 and S2 are closed.
FigureAns : When both S1 and S2 are closed, the circuit forms a balanced a Wheatstone bridge and no current flows along ad. Thus, i = 0.
Page No 307:
- Qstn #20Figure shows a circular coil of N turns and radius a, connected to a battery of emf ε through a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a‘ and resistance r‘ is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instantAns :
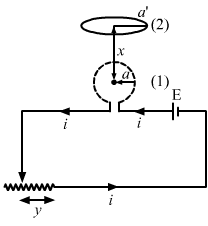
The magnetic field due to coil 1 at the centre of coil 2 is given by
`` B=\frac{{\,\mathrm{\,\mu \,}}_{0}Ni{a}^{2}}{2({a}^{2}+{x}^{2}{)}^{3/2}}``
The flux linked with coil 2 is given by
`` \varphi =B.A\text{'}=\frac{{\,\mathrm{\,\mu \,}}_{0}Ni{a}^{2}}{2({a}^{2}+{x}^{2}{)}^{3/2}}\,\mathrm{\,\pi \,}a{\text{'}}^{2}``
Now, let y be the distance of the sliding contact from its left end.
Given:
`` v=\frac{dy}{dt}``
Total resistance of the rheostat = R
When the distance of the sliding contact from the left end is y, the resistance of the rheostat (R') is given by
`` R\text{'}=\frac{R}{L}y``
The current in the coil is the function of distance y travelled by the sliding contact of the rheostat. It is given by
`` i=\frac{\epsilon }{\left({\displaystyle \frac{R}{L}}y+r\right)}``
The magnitude of the emf induced can be calculated as:
`` e=\frac{d\,\mathrm{\,\varphi \,}}{dt}=\frac{{\mu }_{0}N{a}^{2}a{\text{'}}^{2}\,\mathrm{\,\pi \,}}{2({a}^{2}+{x}^{2}{)}^{3/2}}\frac{di}{dt}``
`` ``
`` \Rightarrow e=\frac{{\,\mathrm{\,\mu \,}}_{0}N\,\mathrm{\,\pi \,}{a}^{2}a{\text{'}}^{2}}{2({a}^{2}+{x}^{2}{)}^{3/2}}\frac{d}{dt}\frac{\epsilon }{\left({\displaystyle \frac{R}{L}}y+r\right)}``
`` \Rightarrow e=\frac{{\,\mathrm{\,\mu \,}}_{0}N\,\mathrm{\,\pi \,}{a}^{2}a{\text{'}}^{2}}{2({a}^{2}+{x}^{2}{)}^{3/2}}\left[\epsilon \frac{\left(-{\displaystyle \frac{R}{L}}v\right)}{{\left({\displaystyle \frac{R}{L}}y+r\right)}^{2}}\right]``
- #20-athe contact begins to slide andAns : For y = L,
`` e=\frac{{\,\mathrm{\,\mu \,}}_{0}N\,\mathrm{\,\pi \,}{a}^{2}a{\mathit{\text{'}}}^{\mathit{2}}\epsilon Rv}{2L({a}^{2}+{x}^{2}{)}^{3/2}(R+r{)}^{2}}``
- #20-bit has slid through half the length of the rheostat.
FigureAns : For y = L/2,
`` \frac{R}{L}y=\frac{R}{2}``
`` \Rightarrow e=\frac{{\mu }_{0}N\pi {a}^{2}a{\text{'}}^{2}}{2L({a}^{2}+{x}^{2}{)}^{3/2}}\frac{\epsilon Rv}{{\left({\displaystyle \frac{R}{2}}+r\right)}^{2}}``
Page No 307:
- Qstn #21A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s.Ans : Given:
Number of turns of the coil, N = 50
Magnetic field through the circular coil, `` \stackrel{\to }{B}`` = 0.200 T
Radius of the circular coil, r = 2.00 cm = 0.02 m
Angle through which the coil is rotated, θ = 60°
Time taken to rotate the coil, t = 0.100 s