38: Electromagnetic Induction : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

38: Electromagnetic Induction

with Solutions - page 4

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#1-c
dΦBdt. The symbols have their usual meaning.
Ans : The quantity `` \frac{d\,\mathrm{\,\varphi \,}}{dt}`` is equal to the emf induced; thus, its dimensions are the same as that of the voltage.
Voltage can be written as:
`` \,\mathrm{\,Voltage\,}=\frac{\,\mathrm{\,Energy\,}}{\,\mathrm{\,Charge\,}}``
Dimensions of energy = [ML²T^-2]
Dimensions of charge = [IT]
The dimensions of voltage can be written as:
[ML²T^-2] ×[IT]^-1 = [ML²I^-1T^-3]
∴ Dimensions of `` \frac{d\,\mathrm{\,\varphi \,}}{dt}`` = [ML²I^-1T^-3]
Page No 306:

Qstn #2
The flux of magnetic field through a closed conducting loop changes with time according to the equation, Φ = at² + bt + c.
Ans : According to the principle of homogeneity of dimensions, the dimensions of each term on both the sides of a correct equation must be the same.
Now,
ϕ = at² + bt + c

#2-a
Write the SI units of a, b and c.
Ans : The dimensions of the quantities at², bt, c and ϕ must be the same.
Thus, the units of the quantities are as follows:
`` a=\left(\frac{\,\mathrm{\,\varphi \,}}{{t}^{2}}\right)=\left[\frac{\,\mathrm{\,\varphi \,}/t}{t}\right]=\frac{\,\mathrm{\,Volt\,}}{\,\mathrm{\,s\,}}``
`` b=\left[\frac{\,\mathrm{\,\varphi \,}}{t}\right]=\,\mathrm{\,Volt\,}``
`` c=\left[\,\mathrm{\,\varphi \,}\right]=\,\mathrm{\,Weber\,}``

#2-b
If the magnitudes of a, b and c are 0.20, 0.40 and 0.60 respectively, find the induced emf at t = 2 s.
Ans : The emf is written as:
`` E=\frac{d\varphi }{dt}`` = 2at + b = 2 × 0.2 × 2 + 0.4 (∵ a = 0.2, b = 0.4 and c = 0.6)
On substituting t = 2 s, we get
E = 0.8 + 0.4
= 1.2 V
Page No 306:

Qstn #3
(a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10^-3 m² placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
Figure
digAnsr: b
Ans : Given:
Area of the loop = 2.0 × 10^-3 m²

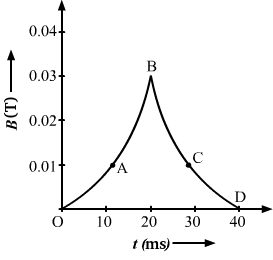
The following conclusions can be made from the graph given above:
The magnetic flux at point O is 0.
The magnetic flux at point A is given by
ϕ₂ = B.A = 0.01 × 2 × 10^-3
= 2 × 10^-5 [∵ ϕ₁ = 0]
The change in the magnetic flux in 10 ms is given by
`` ∆``ϕ = 2 × 10^-5
The emf induced is given by
`` e=\frac{-∆\,\mathrm{\,\varphi \,}}{∆t}=-\left(\frac{2\times {10}^{-5}-0}{10\times {10}^{-3}}\right)=-2\,\mathrm{\,mV\,}``
The magnetic flux at point B is given by
ϕ₃ = B.A = 0.03 × 2 × 10^-3
= 6 × 10^-5
The change in the magnetic flux in 10 ms is given by
`` ∆``ϕ = 6 × 10^-5 - 2 × 10^-5 = 4 × 10^-5
The emf induced is given by
`` e=-\frac{∆\varphi }{∆t}=-4\,\mathrm{\,mV\,}``
The magnetic flux at point C is given by
ϕ₄ = B.A = 0.01 × 2 × 10^-3
= 2 × 10^-5
The change in the magnetic flux in 10 ms is given by
`` ∆``ϕ = (2 × 10^-5 - 6 × 10^-5 ) = - 4 × 10^-5
The emf induced is given by
`` e=-\frac{∆\,\mathrm{\,\varphi \,}}{∆t}=4\,\mathrm{\,mV\,}``
The magnetic flux at point D is given by
ϕ₅ = B.A = 0
The change in the magnetic flux in 10 ms is given by
`` ∆``ϕ = 0 - 2 × 10^-5
The emf induced is given by
`` e=\frac{-∆\varphi }{∆t}=-\frac{(-2)\times {10}^{-5}}{10\times {10}^{-3}}=2\,\mathrm{\,mV\,}``
(b) Emf is not constant in the intervals 10 ms‒20 ms and 20 ms‒30 ms.
Page No 306:

Qstn #4
A conducting circular loop having a radius of 5.0 cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced in the loop during this time.
Ans : Given:
Magnetic field intensity, B = 0.50 T
Radius of the loop, r = 5.0 cm = 5 × 10^-2 m
∴ Area of the loop, A = `` \,\mathrm{\,\pi \,}{r}^{2}``
Initial magnetic flux in the loop, ϕ₁ = B × A
ϕ₁= 0.5 × `` \,\mathrm{\,\pi \,}``(5 × 10^-2)² = 125`` \,\mathrm{\,\pi \,}`` × 10^-5
As the loop is removed from the magnetic field, magnetic flux (ϕ₂) = 0.
Induced emf ε is given by
`` \,\mathrm{\,\epsilon \,}=\frac{{\,\mathrm{\,\varphi \,}}_{1}-{\,\mathrm{\,\varphi \,}}_{2}}{t}``
`` =\frac{125\,\mathrm{\,\pi \,}\times {10}^{-5}}{5\times {10}^{-1}}``
`` =25\,\mathrm{\,\pi \,}\times {10}^{-4}``
= 25 × 3.14 × 10^-4
= 78.5 × 10^-4 V = 7.8 × 10^-3 V

Page No 306:

Qstn #5
A conducting circular loop of area 1 mm² is placed coplanarly with a long, straight wire at a distance of 20 cm from it. The straight wire carries an electric current which changes from 10 A to zero in 0.1 s. Find the average emf induced in the loop in 0.1 s.
Ans : Given:
Area of the loop, A = 1 mm²
Current through the wire, i = 10 A
Separation between the wire and the loop, d = 20 cm
Time, dt = 0.1 s
The average emf induced in the loop is given by
`` e=\frac{\,\mathrm{\,d\varphi \,}}{\,\mathrm{\,d\,}t}``
`` =\frac{BA}{\,\mathrm{\,d\,}t}=\frac{{\mu }_{0}i}{2\pi d}\times \frac{A}{\,\mathrm{\,d\,}t}``
`` =\frac{4\,\mathrm{\,\pi \,}\times {10}^{-7}\times 10}{2\,\mathrm{\,\pi \,}\times 2\times {10}^{-1}}\times \frac{{10}^{-6}}{1\times {10}^{-1}}``
`` =1\times {10}^{-10}\,\mathrm{\,V\,}``
Page No 306:

Qstn #6
A square-shaped copper coil has edges of length 50 cm and contains 50 turns. It is placed perpendicular to a 1.0 T magnetic field. It is removed from the magnetic field in 0.25 s and restored in its original place in the next 0.25 s. Find the magnitude of the average emf induced in the loop during

#6-a
its removal,
Ans : When the coil is removed from the magnetic field:
Initial magnetic flux through the coil, ϕ₁ = BA
∴ ϕ₁ = 50 × 0.5 × 0.5 T-m²
= 12.5 T-m²
Now,
Initial magnetic flux through the coil, ϕ₂ = 0
Time taken, t = 0.25 s
The average emf induced is given by
`` e=-\frac{∆\,\mathrm{\,\varphi \,}}{∆t}=\frac{{\,\mathrm{\,\varphi \,}}_{1}-{\,\mathrm{\,\varphi \,}}_{2}}{dt}``
`` =\frac{12.5-0}{0.25}=\frac{125\times {10}^{-1}}{25\times {10}^{-2}}=50\,\mathrm{\,V\,}``

#6-b
its restoration and
Ans : When the coil is taken back to its original position:
Initial magnetic flux through the coil, ϕ₁ = 0
Initial magnetic flux through the coil, ϕ₂ = 12.5 T-m²
Time taken, t = 0.25 s
The average emf induced is given by
`` e=\frac{12.5-0}{0.25}=50\,\mathrm{\,V\,}``

#6-c
its motion.
Ans : When the coil is moving outside the magnetic field:
Initial magnetic flux, ϕ₁ = 0
Final magnetic flux, ϕ₂ = 0
Because there is no change in the magnetic flux, no emf is induced.
Page No 306:

Qstn #7
Suppose the resistance of the coil in the previous problem is 25â„¦. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during
Ans : Given:
Resistance of the coil, R = 25 Ω

#7-a
its removal,
Ans : During the removal the emf induced in the coil,
e = 50 V
time taken, t = 0.25 s
current in the coil, `` i=\frac{e}{\,\mathrm{\,R\,}}=2\,\mathrm{\,A\,}``
Thus, the thermal energy developed is given by
H = I²RT
= 4 × 25 × 0.25 = 25 J

#7-b
its restoration and
Ans : During the restoration of the coil,
emf induced in it, e = 50 V
time taken, t = 0.25 s
current in the coil, `` i=\frac{e}{\,\mathrm{\,R\,}}=2\,\mathrm{\,A\,}``
Thus, the thermal energy developed is given by
H = i²RT = 25 J

#7-c
its motion.
Ans : We know that energy is a scalar quantity. Also, the net thermal energy is the algebraic sum of the two energies calculated.
∴ Net thermal energy developed
= 25 J + 25 J = 50 J
Page No 306: