NEET-XII-Physics
38: Electromagnetic Induction
- #3(a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10-3 m2 placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
FiguredigAnsr: bAns : Given:
Area of the loop = 2.0 × 10-3 m2
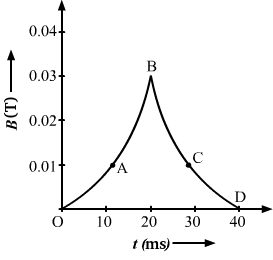
The following conclusions can be made from the graph given above:
The magnetic flux at point O is 0.
The magnetic flux at point A is given by
ϕ2 = B.A = 0.01 × 2 × 10-3
= 2 × 10-5 [∵ ϕ1 = 0]
The change in the magnetic flux in 10 ms is given by
`` ∆``ϕ = 2 × 10-5
The emf induced is given by
`` e=\frac{-∆\,\mathrm{\,\varphi \,}}{∆t}=-\left(\frac{2\times {10}^{-5}-0}{10\times {10}^{-3}}\right)=-2\,\mathrm{\,mV\,}``
The magnetic flux at point B is given by
ϕ3 = B.A = 0.03 × 2 × 10-3
= 6 × 10-5
The change in the magnetic flux in 10 ms is given by
`` ∆``ϕ = 6 × 10-5 - 2 × 10-5 = 4 × 10-5
The emf induced is given by
`` e=-\frac{∆\varphi }{∆t}=-4\,\mathrm{\,mV\,}``
The magnetic flux at point C is given by
ϕ4 = B.A = 0.01 × 2 × 10-3
= 2 × 10-5
The change in the magnetic flux in 10 ms is given by
`` ∆``ϕ = (2 × 10-5 - 6 × 10-5 ) = - 4 × 10-5
The emf induced is given by
`` e=-\frac{∆\,\mathrm{\,\varphi \,}}{∆t}=4\,\mathrm{\,mV\,}``
The magnetic flux at point D is given by
ϕ5 = B.A = 0
The change in the magnetic flux in 10 ms is given by
`` ∆``ϕ = 0 - 2 × 10-5
The emf induced is given by
`` e=\frac{-∆\varphi }{∆t}=-\frac{(-2)\times {10}^{-5}}{10\times {10}^{-3}}=2\,\mathrm{\,mV\,}``
(b) Emf is not constant in the intervals 10 ms‒20 ms and 20 ms‒30 ms.
Page No 306: