32: Electric Current In Conductors : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

32: Electric Current in Conductors

with Solutions - page 6

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

#20-c
R = 10 Ω. Note from your answers that in order to get more current from a combination of two batteries, they should be joined in parallel if the external resistance is small and in series if the external resistance is large, compared to the internal resistance.
Figure 32-E3
Ans : For R = 10 Ω:
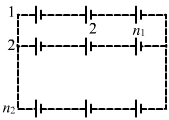
Applying KVL in the circuit given in figure 1, we get:
`` 10{i}_{1}+1{i}_{1}-6+1{i}_{1}-6=0``
`` \Rightarrow 12{i}_{1}=12``
`` \Rightarrow {i}_{1}=1``
`` ``
Now, for figure 2:
Applying KVL in ABCDA, we get:
`` 10{i}_{2}+i-6=0``
`` \Rightarrow i=6-10{i}_{2}``
Applying KVL in ADEFA, we get:
`` i-6+6-\left({i}_{2}-i\right)1=0``
`` \Rightarrow i-{i}_{2}+i=0``
`` \Rightarrow 2i-{i}_{2}=0``
`` \Rightarrow 2\left[6-10{i}_{2}\right]-{i}_{2}=0``
`` \Rightarrow 12-21{i}_{2}=0``
`` \Rightarrow {i}_{2}=0.57\,\mathrm{\,A\,}``
`` \therefore \frac{{i}_{1}}{{i}_{2}}=1.75``
Page No 199:

Qstn #21
Consider N = n₁n₂ identical cells, each of emf ε and internal resistance r. Suppose n₁ cells are joined in series to form a line and n₂ such lines are connected in parallel.
The combination drives a current in an external resistance R.

#21-a
Find the current in the external resistance.
Ans :
Given:
Emf of one cell = E
∴ Total e.m.f. of n₁ cells in one row = n₁E
Total emf of one row will be equal to the net emf across all the n₂ rows because of parallel connection.
Total resistance in one row = n₁r
Total resistance of n₂rows in parallel `` =\frac{{n}_{1}r}{{n}_{2}}``
Net resistance of the circuit = R + `` \frac{{n}_{1}r}{{n}_{2}}``
`` \therefore \,\mathrm{\,Current\,},I=\frac{{n}_{1}E}{R+{\displaystyle \frac{{n}_{1}r}{{n}_{2}}}}=\frac{{n}_{1}{n}_{2}\,\mathrm{\,E\,}}{{n}_{2}\,\mathrm{\,R\,}+{n}_{1}r}``

#21-b
Assuming that n₁ and n₂ can be continuously varied, find the relation between n₁, n₂, R and r for which the current in R is maximum.
Ans : From
(a),
`` I=\frac{{n}_{1}{n}_{2}\,\mathrm{\,E\,}}{{n}_{2}\,\mathrm{\,R\,}+{n}_{1}r}``
For I to be maximum, (n₁r + n₂R) should be minimum
`` \Rightarrow {\left(\sqrt{{n}_{1}r}-\sqrt{{n}_{2}\,\mathrm{\,R\,}}\right)}^{2}+2\sqrt{{n}_{1}\,\mathrm{\,R\,}{n}_{2}r}=\,\mathrm{\,min\,}``
It is minimum when
`` \sqrt{{n}_{1}r}=\sqrt{{n}_{2}\,\mathrm{\,R\,}}``
`` {n}_{1}r={n}_{2}\,\mathrm{\,R\,}``
∴ I is maximum when n₁r = n₂R .
Page No 199:

Qstn #22
A battery of emf 100 V and a resistor of resistance 10 kΩ are joined in series. This system is used as a source to supply current to an external resistance R. If R is not greater than 100 Ω, the current through it is constant up to two significant digits.
Find its value. This is the basic principle of a constant-current source.
Ans : Given:
Emf of the battery, E = 100 volt
Resistance in series with battery, R' = 10 kΩ = 10000 Ω
External resistance, R = (1-100) Ω
When no external resistor is present (R = 0), current through the circuit,
`` i=\frac{\,\mathrm{\,E\,}}{\,\mathrm{\,R\,}\mathit{\text{'}}}=\frac{100}{1000}=0.01\,\mathrm{\,Amp\,}.``
`` ``
When R = 1 Ω,
`` i=\frac{100}{10000+1}=\frac{100}{10001}``
`` =0.009999\,\mathrm{\,A\,}``
When R = 100 Ω,
`` i=\frac{100}{10000+100}``
`` =\frac{100}{10100}=0.009900\,\mathrm{\,A\,}``
We can see that up to R = 100 Ω, the current does not change up to two significant digits.
Page No 199:

Qstn #23
If the reading of the ammeter, A₁ in the figure (32-E4) is 2.4 A, what will be the readings of ammeters A₂ and A₃? Neglect the resistances of the ammeters.
figure 32-E4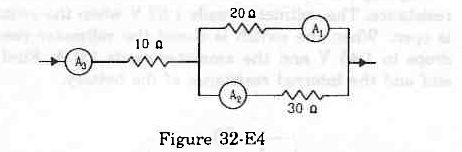
Ans :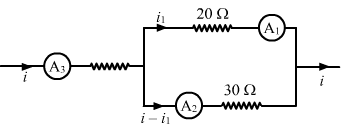
Given: i₁ = 2.4 A
Since the 20 Ω and 30 Ω resistors are connected in parallel, the voltage across them will be the same.
From the figure,
`` 20{i}_{1}=30\left(i-{i}_{1}\right)``
`` \Rightarrow 50{i}_{1}=30i``
`` \Rightarrow i=\frac{50{i}_{1}}{30}=3.99=4\,\mathrm{\,A\,}``
`` ``
∴ The reading of ammeter A3 = i = 4 A
The reading of ammeter A2 = i - i₁ = 1.6 A
Page No 199:

Qstn #24
The resistance of the rheostat shown in the figure (32-E5) is 30 Ω. Neglecting the meter resistance, find the
figure32-E5
minimum and maximum currents through the ammeter as the rheostat is varied.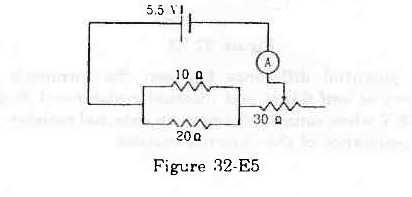
Ans : Current will be minimum when the rheostat will have maximum resistance, i.e 30 Ω.
In this case, total resistance of the circuit = `` \frac{20\times 10}{30}+30=36.67\,\mathrm{\,\Omega \,}``
The minimum current through the circuit,
`` {i}_{\,\mathrm{\,min\,}}=\frac{5.5}{36.67}=0.15\,\mathrm{\,A\,}``
Current will be maximum when the rheostat will have minimum resistance, i.e. 0 Ω.
In this case, total resistance of the circuit = `` \frac{20\times 10}{30}=6.67\,\mathrm{\,\Omega \,}``
The maximum current through the circuit,
`` {i}_{\,\mathrm{\,max\,}}=\frac{5.5}{6.67}=0.825\,\mathrm{\,A\,}``
Page No 199:

Qstn #25
Three bulbs, each with a resistance of 180 Ω, are connected in parallel to an ideal battery of emf 60 V.
Find the current delivered by the battery when

#25-a
all the bulbs are switched on,
Ans : When all the bulbs are switched on, we have a combination of three bulbs in parallel.
The effective resistance of the circuit,
`` {R}_{\,\mathrm{\,eff\,}}=\frac{180}{3}=60\,\mathrm{\,\Omega \,}``
`` ``
The current delivered by the battery,
`` i=\frac{60}{60}=1\,\mathrm{\,A\,}``

#25-b
two of the bulbs are switched on and
Ans : When two of the bulbs are switched on, they are parallel to each other.
The effective resistance of the circuit,
`` {R}_{\,\mathrm{\,eff\,}}=\frac{180}{2}=90\,\mathrm{\,\Omega \,}``
The current delivered by the battery,
`` i=\frac{60}{90}=0.67\,\mathrm{\,A\,}``

#25-c
only one bulb is switched on.
Ans : When only one bulb is switched on, the effective resistance of the circuit,
`` {R}_{\,\mathrm{\,eff\,}}=180\,\mathrm{\,\Omega \,}``
`` ``
The current delivered by the battery,
`` i=\frac{60}{180}=0.33\,\mathrm{\,A\,}``
Page No 199:

Qstn #26
Suppose you have three resistors of 20 Ω, 50 Ω and 100 Ω. What minimum and maximum resistance can you obtain from these resistors?
Ans : We can obtain maximum resistance when all the resistors are connected in series.
So, maximum resistance,
`` {R}_{\,\mathrm{\,max\,}}=\left(20+50+100\right)\,\mathrm{\,\Omega \,}=170\,\mathrm{\,\Omega \,}``
The minimum resistance will be obtained when all the resistors are connected in parallel
So, minimum resistance,
`` {R}_{\,\mathrm{\,min\,}}=\frac{1}{{\displaystyle \frac{1}{20}}+{\displaystyle \frac{1}{50}}+{\displaystyle \frac{1}{100}}}=\frac{100}{8}=12.5\,\mathrm{\,\Omega \,}``
Page No 199:

Qstn #27
A bulb is made using two filaments. A switch selects whether the filaments are used individually or in parallel. When used with a 15 V battery, the bulb can be operated at 5 W, 10 W or 15 W. What should be the resistances of the filaments?
Ans : We know:
`` R=\frac{{V}^{2}}{P}``,
where R is the resistance, V is the voltage drop and P is the power on which the bulb is operated.
We can calculate the resistance of the bulb for the same V and different P.
The resistances of the bulb for three different powers are:
`` {R}_{1}=\frac{{\left(15\right)}^{2}}{5}=45\,\mathrm{\,\Omega \,}``
`` {R}_{2}=\frac{{\left(15\right)}^{2}}{10}=22.5\,\mathrm{\,\Omega \,}``
`` {R}_{3}=\frac{{\left(15\right)}^{2}}{15}=15\,\mathrm{\,\Omega \,}``
When the two resistance are used in parallel, the equivalent resistance will be less than their individual resistance.
∴ The two resistance are 45 Ω and 22.5 Ω.
Page No 199:

Qstn #28
Figure (32-E6) shows a part of a circuit. If a current of 12 mA exists in the 5 kΩ resistor, find the currents in the other three resistors. What is the potential difference between the points A and B?
Figure32-E6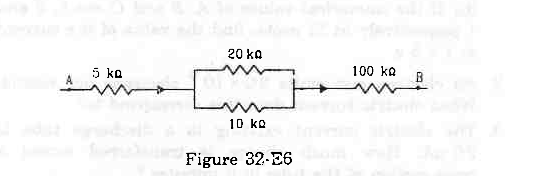
Ans :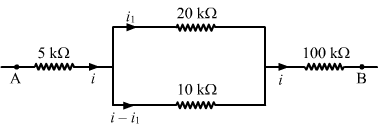
Let the current flowing through the resistors be marked as shown in the figure.
Given: i = 12 mA
The resistors of 20 kΩ and 10 kΩ are connected in parallel. So, the potential difference across their ends will be same, i.e.
`` 20{i}_{1}=10\left(i-{i}_{1}\right)``
`` \Rightarrow 30{i}_{1}=10i``
`` \Rightarrow {i}_{1}=\frac{i}{3}=\frac{12}{3}=4\,\mathrm{\,mA\,}``
∴ The current flowing through the 20 kΩ resistor = i₁ = 4 mA
The current flowing through the 10 kΩ resistor = i - i₁ = 8 mA
From the figure,
The current flowing through the 100 kΩ resistor = i = 12 mA
The equivalent resistance between the points A and B,
`` {R}_{\,\mathrm{\,net\,}}=\left(5+\frac{20\times 10}{20+10}+100\right)\,\mathrm{\,k\Omega \,}=111.67\,\mathrm{\,k\Omega \,}``
The potential difference V between the points A and B,
`` V=i{R}_{\,\mathrm{\,net\,}}``
`` \Rightarrow V=12\times {10}^{-3}\times 111.67\times {10}^{3}=1340\,\mathrm{\,V\,}``
Page No 199:

Qstn #29
An ideal battery sends a current of 5 A in a resistor. When another resistor of 10 Ω is connected in parallel, the current through the battery is increased to 6 A. Find the resistance of the first resistor.
Ans : Let the resistance of the first resistor be R.
If V is the potential difference across R, then the current through it,
`` i=5=\frac{V}{R}``
Now, the other resistor of 10 Ω is connected in parallel with R.
It is given that the new value of current through the circuit, i' = 6 A
The effective resistance of the circuit, R' = `` \frac{10R}{10+R}``
Since the potential difference is constant,
`` iR=i\text{'}R\text{'}``
`` \Rightarrow 5\times R=6\times \frac{10R}{10+R}``
`` \Rightarrow \left(10+R\right)5=60``
`` \Rightarrow 5R=10``
`` \Rightarrow R=2\,\mathrm{\,\Omega \,}``
Page No 199: