32: Electric Current In Conductors : Neet-xii-physics

Home Learn Fast select Course

Change Unit Change Subject Last Menu

NEET-XII-Physics

32: Electric Current in Conductors

with Solutions - page 7

Note: Please signup/signin free to get personalized experience.

10 minutes can boost your percentage by 10%

Note: Please signup/signin free to get personalized experience.

Qstn #30
Find the equivalent resistance of the network shown in the figure (32-E7) between the points a and b.
figure (32-E7)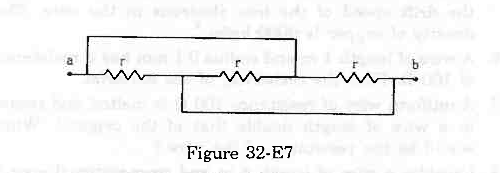
Ans : The simplified circuit can be drawn as shown below.

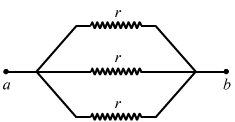
Equivalent resistance `` =\frac{1}{{\displaystyle \frac{1}{r}}+{\displaystyle \frac{1}{r}}+{\displaystyle \frac{1}{r}}}=\frac{r}{3}``
Page No 199:

Qstn #31
A wire of resistance 15.0 Ω is bent to form a regular hexagon ABCDEFA. Find the equivalent resistance of the loop between the points

#31-a
A and B
Ans :
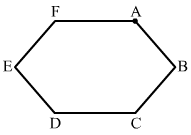
From the figure, it can be seen that between points A and B, the resistance of the first side of the hexagon will be in parallel with the total resistance of the other five sides.
The resistance of the first side can be calculated as shown below.
Resistance of the first leg=`` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{1}{6}}}{{\displaystyle \frac{5}{6}}+{\displaystyle \frac{1}{6}}}\times 15=15\times \frac{1}{6}``
Total resistance of the 5 legs=`` \frac{{\displaystyle \frac{5}{6}}}{{\displaystyle \frac{1}{6}}+{\displaystyle \frac{5}{6}}}\times 15=\frac{5}{6}\times 15``
∴ The effective resistance between the points A and B,
`` {R}_{\,\mathrm{\,eff\,}}=\frac{{\displaystyle \frac{15\times 5}{6}}\times {\displaystyle \frac{15}{6}}}{{\displaystyle \frac{15\times 5}{6}}+{\displaystyle \frac{15}{6}}}=\frac{{\displaystyle \frac{15\times 5\times 15}{6\times 6}}}{{\displaystyle \frac{75+15}{6}}}``
`` =\frac{15\times 5\times 15}{6\times 90}=\frac{25}{12}``
`` =2.08\,\mathrm{\,\Omega \,}``

#31-b
A and C and
Ans : From the figure, it can be seen that between points A and C, the resistance of the first two sides of the hexagon will be in parallel with the total resistance of the other four sides.
Resistance of the two legs =`` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{2}{6}}}{{\displaystyle \frac{4}{6}}+{\displaystyle \frac{2}{6}}}\times 15=15\times \frac{2}{6}``
Total resistance of the four legs=`` \frac{{\displaystyle \frac{4}{6}}}{{\displaystyle \frac{2}{6}}+{\displaystyle \frac{4}{6}}}\times 15=\frac{4}{6}\times 15``
∴ The effective resistance between the points A and C,
`` {\,\mathrm{\,R\,}}_{eff}=\frac{{\displaystyle \frac{15\times 4}{6}}\times {\displaystyle \frac{15\times 2}{6}}}{{\displaystyle \frac{15\times 4}{6}}+{\displaystyle \frac{15\times 2}{6}}}=\frac{{\displaystyle \frac{15\times 4\times 2\times 15}{6\times 6}}}{{\displaystyle \frac{60+30}{6}}}``
`` =\frac{15\times 2\times 4\times 15}{6\times 90}``
`` =\frac{10}{3}=3.33\,\mathrm{\,\Omega \,}``

#31-c
A and D.
Ans : From the figure, it can be seen that between points A and D, the resistance of the first three sides of the hexagon will be in parallel with the total resistance of the other three sides.
Resistance of the three legs = `` \frac{\text{L}\,\mathrm{\,ength\,}\,\mathrm{\,of\,}\,\mathrm{\,the\,}\,\mathrm{\,that\,}\,\mathrm{\,portion\,}}{\text{T}\,\mathrm{\,otal\,}\,\mathrm{\,length\,}}\times R=\frac{{\displaystyle \frac{3}{6}}}{{\displaystyle \frac{3}{6}}+{\displaystyle \frac{3}{6}}}\times 15=15\times \frac{3}{6}``
∴ The effective resistance between the points A and D,
`` {\,\mathrm{\,R\,}}_{\,\mathrm{\,eff\,}}=\frac{{\displaystyle \frac{15\times 3}{6}}\times {\displaystyle \frac{15\times 3}{6}}}{{\displaystyle \frac{15\times 3}{6}}+{\displaystyle \frac{15\times 3}{6}}}=\frac{{\displaystyle \frac{15\times 3\times 3\times 15}{6\times 6}}}{{\displaystyle \frac{90}{6}}}``
`` =\frac{15\times 3\times 3\times 15}{6\times 90}=\frac{15}{4}=3.75\,\mathrm{\,\Omega \,}``
Page No 199:

Qstn #32
Consider the circuit shown in the figure (32-E8). Find the current through the 10 Ω resistor when the switch S is

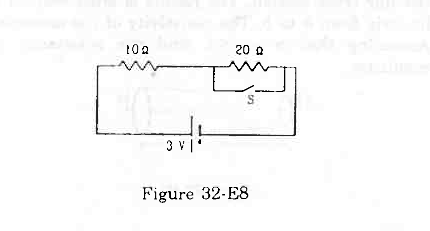
#32-a
open
Ans : When S is open, the resistors will be connected in series, as the current will flow through the 20 Ω resistor. The effective resistance,
`` {\,\mathrm{\,R\,}}_{\,\mathrm{\,eff\,}}=\left(10+20\right)\,\mathrm{\,\Omega \,}=30\,\mathrm{\,\Omega \,}``
`` ``
The current flowing through the circuit,
`` i=\left(\frac{3}{30}\right)\,\mathrm{\,A\,}=0.1\,\mathrm{\,A\,}``

#32-b
closed.
figure32-E8
Ans : When S is closed, current will flow through the switch that offers the least resistive path. So, the 20 Ω resistance will be ineffective in this case. The effective resistance in this case,
`` {R}_{\,\mathrm{\,eff\,}}=10\,\mathrm{\,\Omega \,}``
`` ``
The current flowing through the circuit,
`` i=\left(\frac{3}{10}\right)\,\mathrm{\,A\,}=0.3\,\mathrm{\,A\,}``
Page No 200:

Qstn #33
Find the currents through the three resistors shown in the figure (32-E9).
Figure32-E9
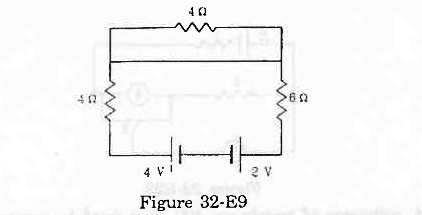
Ans :
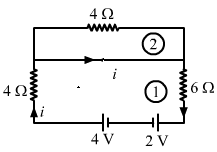
From the figure, we can see that current will flow only in loop 1 because current follows the least resistive path. All the current will pass through the wire connected in parallel to the 4 Ω resistor in loop 2.
∴ There will be no current through the 4 Ω resistor in loop 2.
For loop1, applying KVL, we get:
`` 6i+4i-4+2=0``
`` \Rightarrow 10i=2``
`` \Rightarrow i=0.2\,\mathrm{\,A\,}``
`` ``
∴ The current through the 4 Ω and 6 Ω resistors, i = 0.2 A
Page No 200:

Qstn #34
Figure (32-E10) shows a part of an electric circuit. The potentials at the points a, b and c are 30 V, 12 V and 2 V respectively. Find the currents through the three resistors.
Figure 32-E10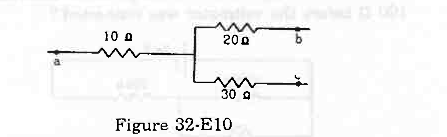
Ans :
Let the potential at the point o be X volts.
From the figure,
`` {i}_{1}=\frac{{V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,o\,}}}{10}``
`` {V}_{\,\mathrm{\,a\,}}=30\,\mathrm{\,V\,}\,\mathrm{\,and\,}{V}_{\,\mathrm{\,o\,}}=X``
`` So,{i}_{1}=\frac{30-X}{10}``
`` \,\mathrm{\,Similarly\,},``
`` {i}_{2}=\frac{{V}_{\,\mathrm{\,o\,}}-{V}_{\,\mathrm{\,b\,}}}{20}``
`` =\frac{X-12}{20}``
`` \,\mathrm{\,And\,}``
`` {i}_{3}=\frac{{V}_{\,\mathrm{\,o\,}}-{V}_{\,\mathrm{\,c\,}}}{30}``
`` =\frac{X-2}{30}``
Also, from kirchoff's junction law we have:
i₁ = i₂ + i₃
`` \Rightarrow \frac{30-X}{10}=\frac{X-12}{20}+\frac{X-2}{30}``
`` \Rightarrow 30-X=\frac{X-12}{2}+\frac{X-2}{3}``
`` \Rightarrow 30-X=\frac{3X-36+2X-4}{6}``
`` \Rightarrow 180-6X=5X-40``
`` \Rightarrow 11X=220``
`` \Rightarrow X=\frac{220}{11}=20\,\mathrm{\,V\,}``
Thus, the currents through the three resistors are:
`` {i}_{1}=\frac{30-20}{10}=1\,\mathrm{\,A\,}``
`` {i}_{2}=\frac{20-12}{20}=\frac{8}{20}=0.4\,\mathrm{\,A\,}``
`` {i}_{3}=\frac{20-2}{30}=\frac{18}{30}=0.6\,\mathrm{\,A\,}``
Page No 200:

Qstn #35
Each of the resistors shown in the figure (32-E11) has a resistance of 10 Ω and each of the batteries has an emf of 10 V. Find the currents flowing through the resistors a and b in the two circuits.
figure 32-E11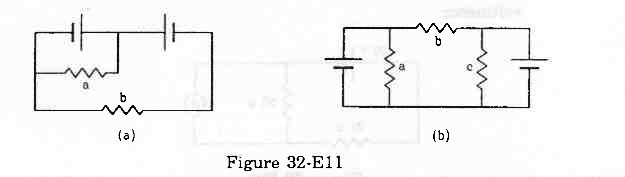
Ans : (a)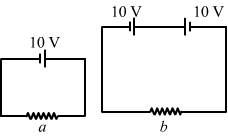
From the figure,
Potential difference between the two ends of resistor a = 10 V
Resistance of resistor a =10 Ω
∴ Current through a = `` \frac{10}{10}=1\,\mathrm{\,A\,}``
Since the two batteries are connected opposite each other,
potential difference between the terminals of b = 10 - 10 = 0 V
∴ Current through b = 0 A
(b)

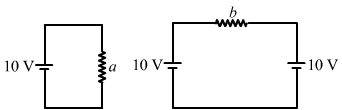
From the figure,
Potential difference between the two ends of resistor a = 10 V.
Resistance of resistor a =10 Ω
∴ Current through a = `` \frac{10}{10}=1\,\mathrm{\,A\,}``
Since the two batteries are again connected opposite to each other,
Potential difference between terminal of b = 10 - 10 = 0 V
∴ Current through b = 0 A
Page No 200:

Qstn #36
Find the potential difference V_a - V_b in the circuits shown in the figure (32-E12).
figure 32-12
Ans :
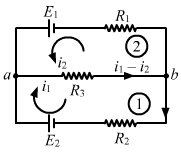
Applying KVL in loop 1, we get:
`` {i}_{1}{R}_{2}-{E}_{2}+\left({i}_{1}+{i}_{2}\right){R}_{3}=0``
`` ({R}_{2}+{R}_{3}){i}_{1}+{R}_{3}{i}_{2}={E}_{2}...\left(1\right)``
Applying KVL in loop 2, we get:
`` {i}_{2}{R}_{1}-{E}_{1}+\left({i}_{1}+{i}_{2}\right){R}_{3}=0``
`` \left({R}_{1}+{R}_{3}\right){i}_{2}+{R}_{3}{i}_{1}={E}_{1}...\left(2\right)``
Multiplying equation (1) by (R₁+R₃) and (2) by R₃ and then subtracting (2) from (1), we get:
`` {i}_{1}=\frac{{E}_{2}\left({R}_{1}+{R}_{3}\right)-{E}_{1}{R}_{3}}{\left({R}_{1}{R}_{2}+{R}_{2}{R}_{3}+{R}_{3}{R}_{1}\right)}``
Similarly, multiplying equation (1) by R₃ and (2) by (R₁+R₃), and then subtracting (2) from (1), we get:
`` {i}_{2}=\frac{{E}_{1}\left({R}_{2}+{R}_{3}\right)-{E}_{2}{R}_{3}}{\left({R}_{1}{R}_{2}+{R}_{2}{R}_{3}+{R}_{3}{R}_{1}\right)}``
From the figure,
`` {V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,b\,}}=\left({i}_{1}+{i}_{2}\right){R}_{3}``
`` \Rightarrow {V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,b\,}}=\left[\frac{{E}_{1}{R}_{2}+{E}_{2}{R}_{1}}{\left({R}_{1}{R}_{2}+{R}_{2}{R}_{3}+{R}_{3}{R}_{1}\right)}\right]{R}_{3}``
`` \Rightarrow {V}_{\,\mathrm{\,a\,}}-{V}_{\,\mathrm{\,b\,}}=\frac{{\displaystyle \frac{{E}_{1}}{{R}_{1}}}+{\displaystyle \frac{{E}_{2}}{{R}_{2}}}}{{\displaystyle \frac{1}{{R}_{1}}}+{\displaystyle \frac{1}{{R}_{2}}}+{\displaystyle \frac{1}{{R}_{3}}}}``
(b) The circuit in figure b can be redrawn as shown below:

We can see that it is similar to the circuit in figure a and, hence, the answer obtained will be same.
Page No 200:

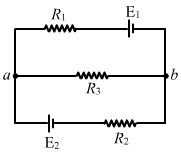
Qstn #37
In the circuit shown in the figure (32-E13), ε₁ = 3 V, ε₂ = 2 V, ε_a = 1 V and r₁ = r₂ = r₃ = 1Ω. Find the potential difference between the points A and B and the current through each branch.
figure 32-E13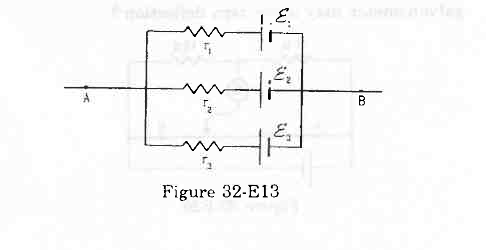
Ans :
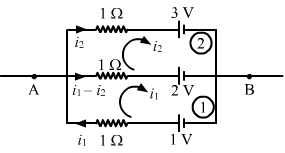
Applying KVL in loop 1, we get:
`` {i}_{1}+\left({i}_{1}-{i}_{2}\right)-1+2=0``
`` 2{i}_{1}-{i}_{2}=-1...\left(1\right)``
`` ``
Similarly, for loop 2:
`` {i}_{2}-\left({i}_{1}-{i}_{2}\right)-2+3=0``
`` 2{i}_{2}-{i}_{1}=-1...\left(2\right)``
Solving (1) and (2), we get:
`` {i}_{1}={i}_{2}=1\,\mathrm{\,A\,}``
`` ``
Potential difference between A and B:
`` {V}_{\,\mathrm{\,A\,}}-{V}_{\,\mathrm{\,B\,}}={E}_{2}-\left({i}_{1}-{i}_{2}\right)\times 1=2-\left(1-1\right)=2\,\mathrm{\,V\,}``
Current through the top branch = i₂ = 1 A
Current through the middle branch = i₁ - i₂ = 0 A
Current through the bottom branch = i₁ = 1 A
Page No 200:

Qstn #38
Find the current through the 10 Ω resistor shown in the figure (32-E14).
Figure 32-E14
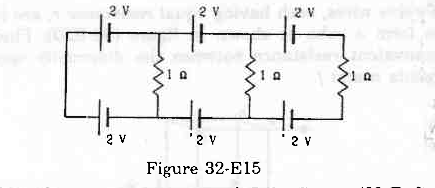
Ans :
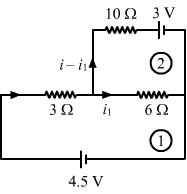
Applying KVL in loop 1, we get:
3i + 6i₁ = 4.5 ...(1)
Applying KVL in loop 2, we get:
`` \left(i-{i}_{1}\right)10+3-6{i}_{1}=0``
`` 10i-16{i}_{1}=-3...\left(2\right)``
`` ``
Multiplying equation (1) by 10 and (2) by 3 and then, subtracting (2) from (1), we get:
`` -108{i}_{1}=-54``
`` \Rightarrow {i}_{1}=\frac{54}{108}=\frac{1}{2}=0.5``
`` ``
Substituting the value of i₁ in (1), we get:
`` 3i+6\times \frac{1}{2}-4.5=0``
`` 3i-1.5=0``
`` \Rightarrow i=\frac{1.5}{3}=0.5``
So, current flowing through the 10 Ω resistor = i - i₁ = 0.5 - 0.5 = 0 A
Page No 200:

Qstn #39
Find the circuit in the three resistors shown in the figure (32-E15).
figure 32-E15
Ans :
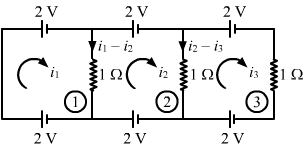
Applying KVL in loop 1, we get:
`` 2+\left({i}_{1}-{i}_{2}\right)\times 1-2=0``
`` \Rightarrow {i}_{1}={i}_{2}``
Applying KVL in loop 2, we get:
`` 2+\left({i}_{2}-{i}_{3}\right)\times 1-2-\left({i}_{1}-{i}_{2}\right)\times 1=0``
`` \Rightarrow {i}_{2}-{i}_{3}-{i}_{1}+{i}_{2}=0``
`` {i}_{1}={i}_{2}``
`` \Rightarrow {i}_{2}-{i}_{3}-{i}_{2}+{i}_{2}=0``
`` \Rightarrow {i}_{2}={i}_{3}``
Applying KVL in loop 3, we get:
`` 2+{i}_{3}-2-\left({i}_{2}-{i}_{3}\right)=0``
`` \Rightarrow {i}_{3}=0``
`` {i}_{1}={i}_{2}={i}_{3}``
`` \therefore {i}_{1}={i}_{2}={i}_{3}=0``
Page No 200: