NEET-XII-Physics
31: Capacitors
- #20Each capacitor shown in figure (31-E10) has a capacitance of 5⋅0 µF. The emf of the battery is 50 V. How much charge will flow through AB if the switch S is closed?
Figure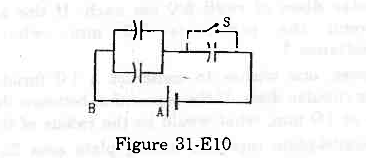 Ans : Initially, when the switch S is open, the equivalent capacitance is given by
Ans : Initially, when the switch S is open, the equivalent capacitance is given by
`` {C}_{\,\mathrm{\,eq\,}}=\frac{2C\times C}{3\,\mathrm{\,C\,}}``
`` \Rightarrow {C}_{\,\mathrm{\,eq\,}}=\frac{2}{3}C=\frac{2}{3}\times 5.0\,\mathrm{\,\mu F\,}``
The charge supplied by the battery is given by
`` Q={C}_{\,\mathrm{\,eq\,}}\times V``
`` \Rightarrow Q=\frac{2}{3}\times (5.0\,\mathrm{\,\mu F\,})\times (50\,\mathrm{\,V\,})``
`` \Rightarrow Q=\frac{500}{3}\,\mathrm{\,\mu C\,}``
When the switch S is closed, no charge goes to the capacitor connected in parallel with the switch.
Thus, the equivalent capacitance is given by
`` {C}_{\,\mathrm{\,eq\,}}=2C=2\times 5.0=10\,\mathrm{\,\mu F\,}``
The charge supplied by the battery is given by
`` Q=10\,\mathrm{\,\mu F\,}\times 50=500\,\mathrm{\,\mu C\,}``
The initial charge stored in the shorted capacitor starts discharging."?
Hence, the charge that flows from A to B is given by
`` {Q}_{\,\mathrm{\,net\,}}=500\,\mathrm{\,\mu C\,}-\frac{500}{3}\,\mathrm{\,\mu C\,}``
`` \Rightarrow {Q}_{\,\mathrm{\,net\,}}=3.3\times {10}^{-4}\,\mathrm{\,C\,}``
Page No 166: